Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу 7- сынып

1 слайд
Екі айнымалысы бар сызықтық теңдеулер жүйесін графиктік тәсілмен шешу Біз бүгін сызықтық теңдеулер жүйесін графиктік тәсілмен шешудің маңыздылығы туралы зерделейміз. Бұл әдісті қолданудың алгоритмін, артықшылықтары мен кемшіліктерін талқылаймыз.

1 слайд

2 слайд
Сызықтық теңдеулер жүйесі дегеніміз не? 1 Сызықтық теңдеулер жүйесі Бір немесе одан да көп сызықтық теңдеулерден тұратын математикалық модель. 2 Екі айнымалысы бар жүйесі Екі сызықтық теңдеуден және екі белгісіз айнымалыдан тұратын жүйесі. 3 Графиктік шешім Теңдеулер жүйесін графиктік тәсілмен шешу және оның шешімдерін табу.

2 слайд

3 слайд
Екі айнымалысы бар сызықтық теңдеулер жүйесінің графиктік шешімі Графиктік Әдіс Әр теңдеуді жеке жазықтықта сызық түрінде көрсетіп, олардың қиылысу нүктесі - жүйенің шешімі. Қиылысу Нүктесі Екі сызық қиылысқан жерде, яғни олардың координаттары - жүйенің жалғыз шешімі.

3 слайд

4 слайд
Графиктік тәсілді қолдану алгоритмі 1 1. Теңдеулерді жазу Екі айнымалысы бар сызықтық теңдеулерді жазу. 2 2. Координат жазықтығында сызу Әр теңдеуді координат жазықтығында сызықтар түрінде көрсету. 3 3. Қиылысу нүктесін табу Сызықтар қиылысатын нүктені анықтау - ол жүйенің шешімі.

4 слайд

5 слайд
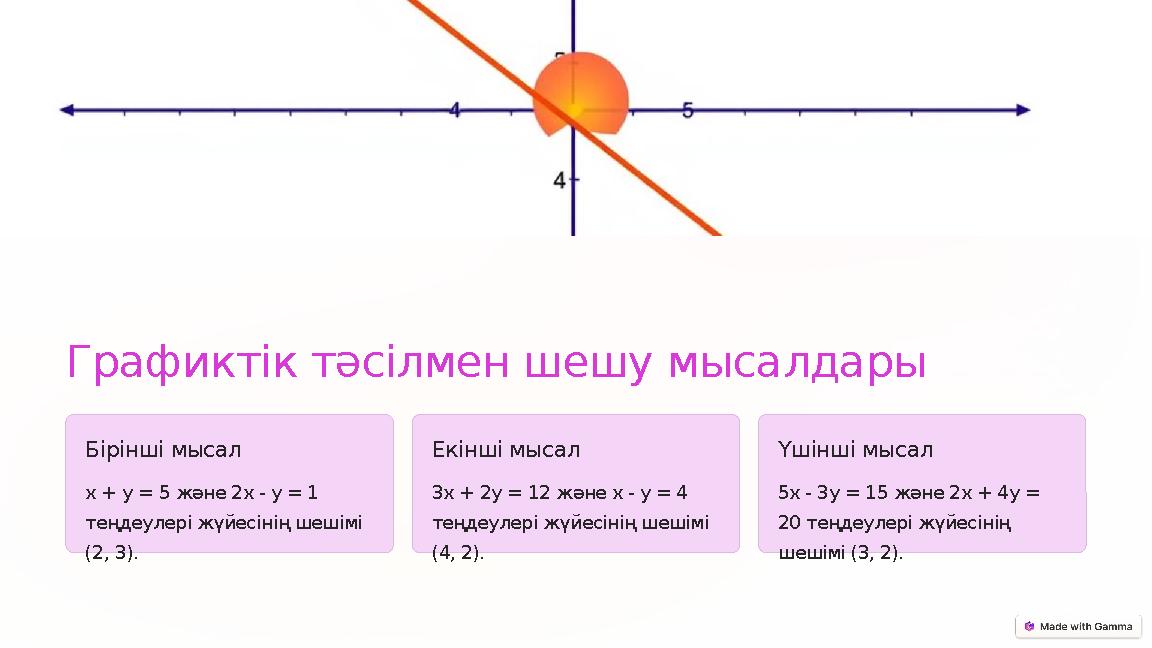
Графиктік тәсілмен шешу мысалдары Бірінші мысал x + y = 5 және 2x - y = 1 теңдеулері жүйесінің шешімі (2, 3). Екінші мысал 3x + 2y = 12 және x - y = 4 теңдеулері жүйесінің шешімі (4, 2). Үшінші мысал 5x - 3y = 15 және 2x + 4y = 20 теңдеулері жүйесінің шешімі (3, 2).

5 слайд

6 слайд
Графиктік шешімнің ерекшеліктері Бірегей шешім Теңдеулер жүйесі бір, жалғыз шешімге ие болуы мүмкін. Шешімсіз жүйе Теңдеулер жүйесінің шешімі болмауы да мүмкін, яғни сызықтар үйлеспесе. Шексіз көп шешім Теңдеулер жүйесінің шешімі шексіз болуы мүмкін, яғни сызықтар тұйықталып өтсе.

6 слайд

7 слайд
Графиктік тәсілдің артықшылықтары мен кемшіліктері Артықшылықтары Жеңіл түсінуге болады, визуалды, интуитивті және қолдануға ыңғайлы. Кемшіліктері Дәлдігі шектеулі, үлкен жүйелер үшін қиын және қолмен есептеулер қажет.

7 слайд

8 слайд
Қорытынды және практикалық ұсыныстар Қорытынды Графиктік тәсіл - екі айнымалысы бар сызықтық теңдеулер жүйесін шешудің пайдалы және түсінікті әдісі. Ұсыныстар Күрделі жағдайларда аналитикалық әдісті пайдалану ұсынылады, ал қарапайым жағдайларда графиктік әдісті қолданыңыз. Практикалық қолдану Графиктік тәсілді есептеу техникасы, физика, геометрия және басқа да пәндерде қолдануға болады.

8 слайд