Ашық сабақ, ҚМЖ, көрнекілік, презентация жариялап
2 млн. ₸ табыс табыңыз!
МИНИСТРЛІКПЕН КЕЛІСІЛГЕН КУРСҚА ҚАТЫСЫП, АТТЕСТАЦИЯҒА ЖАРАМДЫ СЕРТИФИКАТ АЛЫҢЫЗ!
Сертификат Аттестацияға 100% жарамды
ТОЛЫҚ АҚПАРАТ АЛУ 
Функцияның өсу және кему белгілері
Материал туралы қысқаша түсінік
математика пәні мұғалімдеріне ауадай қажет материал
Авторы:
Автор материалды ақылы түрде жариялады.
Сатылымнан түскен қаражат авторға автоматты түрде аударылады.
Толығырақ
09 Ақпан 2021
1862
0 рет жүктелгенТегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!
Дипломдар мен сертификаттарды алып үлгеріңіз!
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 23
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
ФУНКЦИЯНЫҢ
ӨСУ ЖӘНЕ
КЕМУ БЕЛГІЛЕРІ
1 слайд
ФУНКЦИЯНЫҢ ӨСУ ЖӘНЕ КЕМУ БЕЛГІЛЕРІ
2 слайд
О қу мақсаттары:
- функцияның аралықта өсуінің (кемуінің) қажетті және жеткілікті шартын білу;
- функцияның өсу (кему) аралықтарын табу;
Бағалау критерийлері :
- функцияның аралықтағы өсуінің (кемуінің) қажетті және жеткілікті
шарттарын біледі;
- функцияның өсу (кему) аралықтарын таба алады;
2 слайд
О қу мақсаттары: - функцияның аралықта өсуінің (кемуінің) қажетті және жеткілікті шартын білу; - функцияның өсу (кему) аралықтарын табу; Бағалау критерийлері : - функцияның аралықтағы өсуінің (кемуінің) қажетті және жеткілікті шарттарын біледі; - функцияның өсу (кему) аралықтарын таба алады;
![ФУНКЦИЯНЫҢ ӨСУІ ЖӘНЕ КЕМУІ Тауға көтерілді. [b ; a] аралығында функция өспелі Таудан төмен түсіп келеді. [a ;с ] арал](https://api.ust.kz/storage/files/materials/pptx/image/2021/february/d09/1612874939-3.jpeg "ФУНКЦИЯНЫҢ ӨСУІ ЖӘНЕ КЕМУІ Тауға көтерілді. [b ; a] аралығында функция өспелі Таудан төмен түсіп келеді. [a ;с ] арал")
3 слайд
ФУНКЦИЯНЫҢ ӨСУІ ЖӘНЕ КЕМУІ
Тауға көтерілді.
[b ; a] аралығында
функция өспелі Таудан төмен түсіп келеді.
[a ;с ] аралығында функция
кемімелі
0 a
b c
xy
3 слайд
ФУНКЦИЯНЫҢ ӨСУІ ЖӘНЕ КЕМУІ Тауға көтерілді. [b ; a] аралығында функция өспелі Таудан төмен түсіп келеді. [a ;с ] аралығында функция кемімелі 0 a b c xy
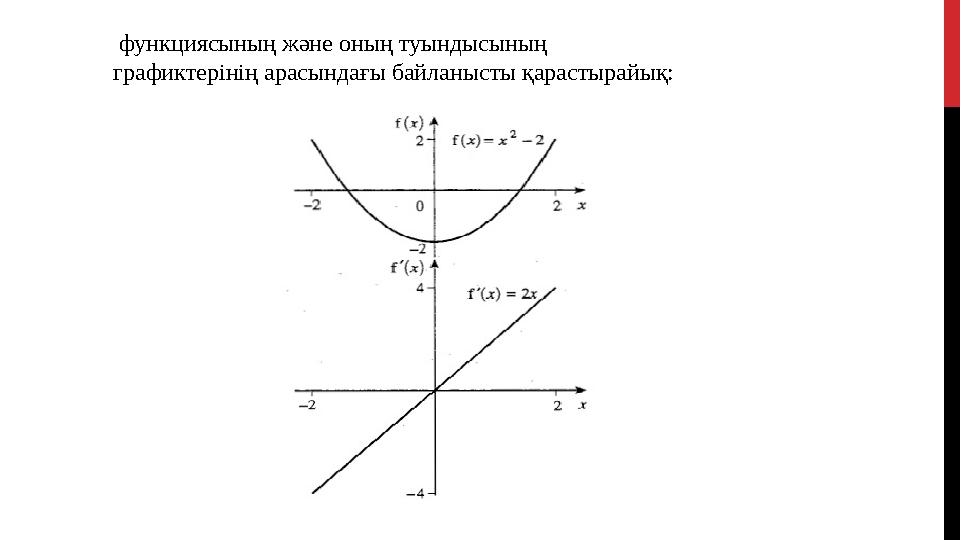
4 слайд
функциясының және оның туындысының
графиктерінің арасындағы байланысты қарастырайық:
4 слайд
функциясының және оның туындысының графиктерінің арасындағы байланысты қарастырайық:
5 слайд
1. Функция туындысының графигі Ох осінен жоғары
орналасатын х нүктелерінің жиыны функция графигінің
өсу аралығындағы х нүктелерінің жиынына сәйкес
келеді.
2. Функция туындысының графигі Ох осінен төмен
орналасатын х нүктелерінің жиыны функция графигінің
кему аралығындағы х нүктелерінің жиынына сәйкес
келеді. Қорытындылар:
5 слайд
1. Функция туындысының графигі Ох осінен жоғары орналасатын х нүктелерінің жиыны функция графигінің өсу аралығындағы х нүктелерінің жиынына сәйкес келеді. 2. Функция туындысының графигі Ох осінен төмен орналасатын х нүктелерінің жиыны функция графигінің кему аралығындағы х нүктелерінің жиынына сәйкес келеді. Қорытындылар:
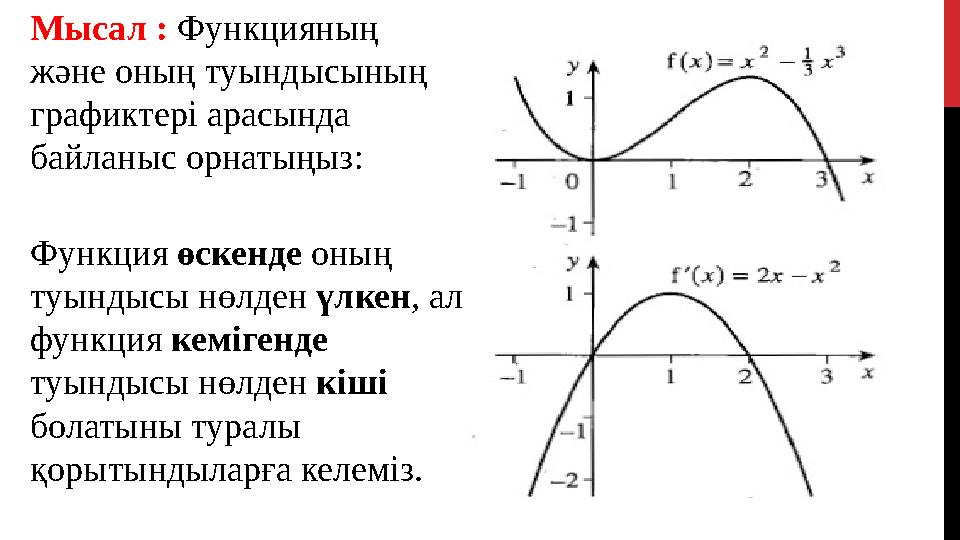
6 слайд
Мысал : Функцияның
және оның туындысының
графиктері арасында
байланыс орнатыңыз:
Функция өскенде оның
туындысы нөлден үлкен , ал
функция кемігенде
туындысы нөлден кіші
болатыны туралы
қорытындыларға келеміз.
6 слайд
Мысал : Функцияның және оның туындысының графиктері арасында байланыс орнатыңыз: Функция өскенде оның туындысы нөлден үлкен , ал функция кемігенде туындысы нөлден кіші болатыны туралы қорытындыларға келеміз.
7 слайд
ФУНКЦИЯНЫҢ ӨСУ, КЕМУІНІҢ ЖЕТКІЛІКТІ
ШАРТЫ
Егер (а; b)
аралығындағы әрбір
х нүктесі үшін
шарты (f
'(x)>0)
орындалатын
болса, онда
үзіліссіз f(x)
функциясы сол
аралықта өспелі
болады. Егер (а; b)
аралығындағы әрбір х
нүктесі үшін (f '(x)<0)
шарты
орындалатын болса,
онда үзіліссіз f(x)
функциясы сол
аралықта кемімелі
болады.
7 слайд
ФУНКЦИЯНЫҢ ӨСУ, КЕМУІНІҢ ЖЕТКІЛІКТІ ШАРТЫ Егер (а; b) аралығындағы әрбір х нүктесі үшін шарты (f '(x)>0) орындалатын болса, онда үзіліссіз f(x) функциясы сол аралықта өспелі болады. Егер (а; b) аралығындағы әрбір х нүктесі үшін (f '(x)<0) шарты орындалатын болса, онда үзіліссіз f(x) функциясы сол аралықта кемімелі болады.
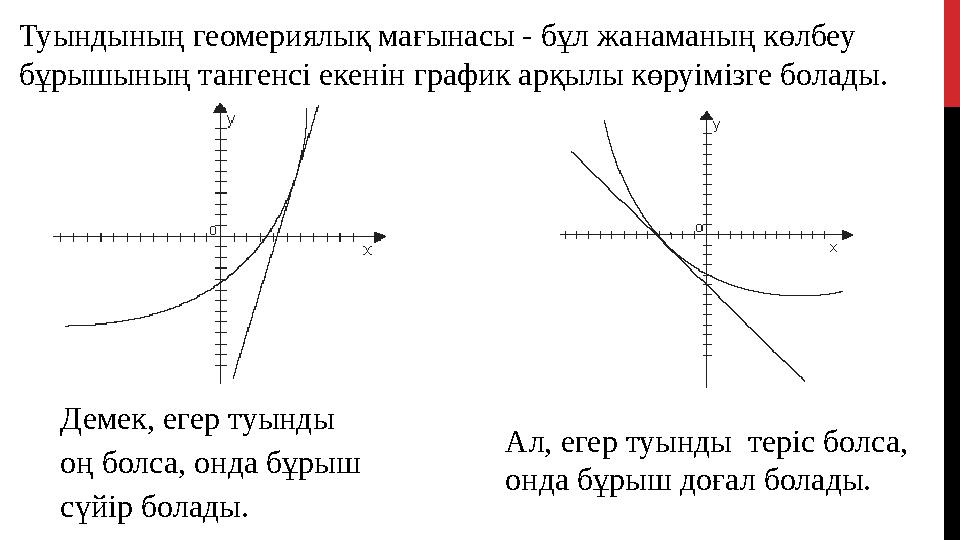
8 слайд
Демек, егер туынды
оң болса, онда бұрыш
сүйір болады.Туындының геомериялық мағынасы - бұл жанаманың көлбеу
бұрышының тангенсі екенін график арқылы көруімізге болады.
Ал, егер туынды теріс болса,
онда бұрыш доғал болады.
8 слайд
Демек, егер туынды оң болса, онда бұрыш сүйір болады.Туындының геомериялық мағынасы - бұл жанаманың көлбеу бұрышының тангенсі екенін график арқылы көруімізге болады. Ал, егер туынды теріс болса, онда бұрыш доғал болады.
9 слайд
Өсу және кему аралықтарын функцияның
монотонды аралықтары деп атаймыз.
9 слайд
Өсу және кему аралықтарын функцияның монотонды аралықтары деп атаймыз.
10 слайд
ФУНКЦИЯНЫ МОНОТОНДЫҚҚА
ЗЕРТТЕУ ТӘСІЛДЕРІ
1 тәсіл.
Функциялардың өсу (кему) анықтамалары бойынша.
2 тәсіл.
Функцияның графигі бойынша.
3 тәсіл.
Функцияның туындысы бойынша.
10 слайд
ФУНКЦИЯНЫ МОНОТОНДЫҚҚА ЗЕРТТЕУ ТӘСІЛДЕРІ 1 тәсіл. Функциялардың өсу (кему) анықтамалары бойынша. 2 тәсіл. Функцияның графигі бойынша. 3 тәсіл. Функцияның туындысы бойынша.
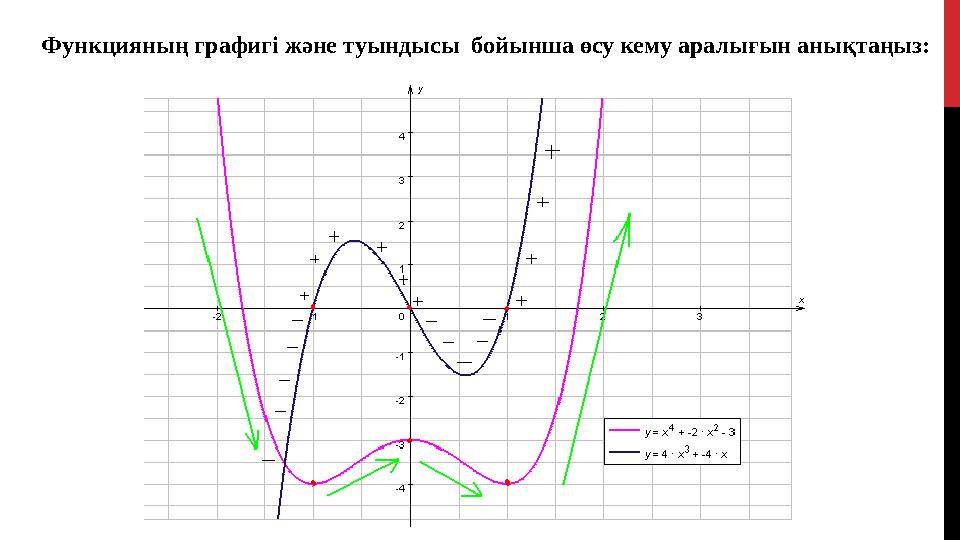
11 слайд
Функцияның графигі және туындысы бойынша өсу кему аралығын анықтаңыз:
11 слайд
Функцияның графигі және туындысы бойынша өсу кему аралығын анықтаңыз:
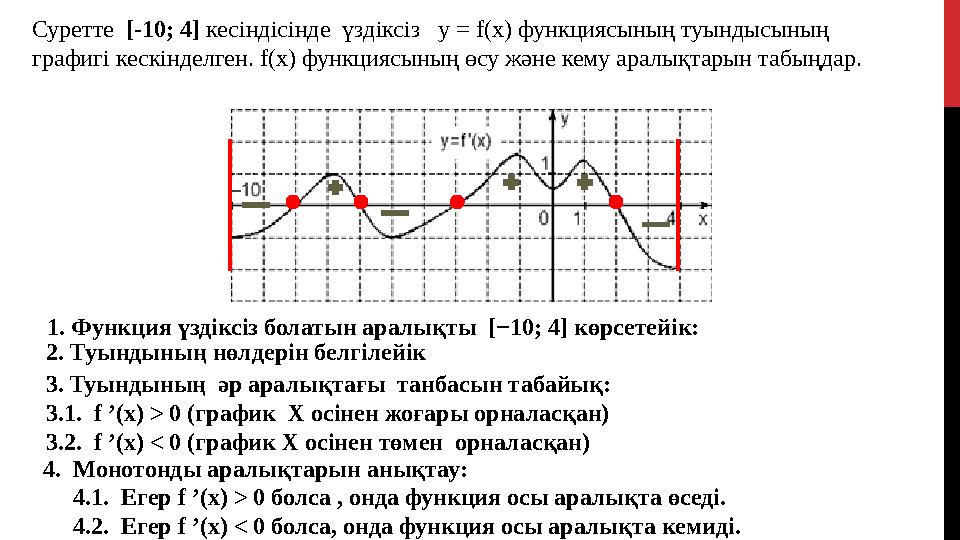
12 слайд
2. Туындының нөлдерін белгілейік
4. Монотонды аралықтарын анықтау:
4.1. Егер f ’(x) > 0 болса , онда функция осы аралықта өседі.
4.2. Егер f ’(x) < 0 болса, онда функция осы аралықта кемиді. Суретте [-1 0 ; 4 ] кесіндісінде үздіксіз y = f(x) функциясының туындысының
графигі кескінделген. f(x) функциясының өсу және кему аралықтарын табыңдар.
1. Функция үздіксіз болатын аралықты [−10; 4] көрсетейік:
3. Туындының әр аралықтағы танбасын табайық:
3.1. f ’(x) > 0 (график Х осінен жоғары орналасқан)
3.2. f ’(x) < 0 (график Х осінен төмен орналасқан)
12 слайд
2. Туындының нөлдерін белгілейік 4. Монотонды аралықтарын анықтау: 4.1. Егер f ’(x) > 0 болса , онда функция осы аралықта өседі. 4.2. Егер f ’(x) < 0 болса, онда функция осы аралықта кемиді. Суретте [-1 0 ; 4 ] кесіндісінде үздіксіз y = f(x) функциясының туындысының графигі кескінделген. f(x) функциясының өсу және кему аралықтарын табыңдар. 1. Функция үздіксіз болатын аралықты [−10; 4] көрсетейік: 3. Туындының әр аралықтағы танбасын табайық: 3.1. f ’(x) > 0 (график Х осінен жоғары орналасқан) 3.2. f ’(x) < 0 (график Х осінен төмен орналасқан)
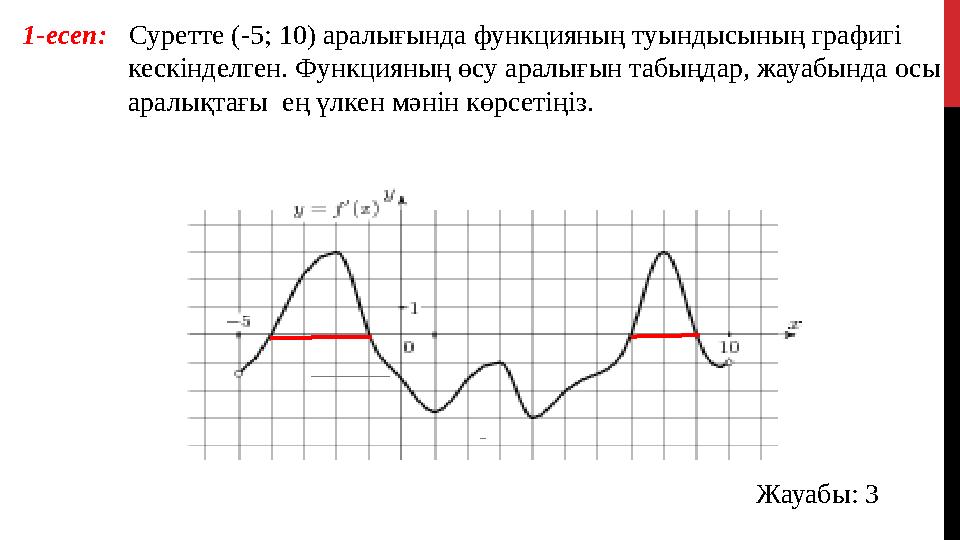
13 слайд
Суретте (-5; 10) аралығында функцияның туындысының графигі
кескінделген. Функцияның өсу аралығын табыңдар, жауабында осы
аралықтағы ең үлкен мәнін көрсетіңіз.
Жауабы : 31-есеп:
13 слайд
Суретте (-5; 10) аралығында функцияның туындысының графигі кескінделген. Функцияның өсу аралығын табыңдар, жауабында осы аралықтағы ең үлкен мәнін көрсетіңіз. Жауабы : 31-есеп:
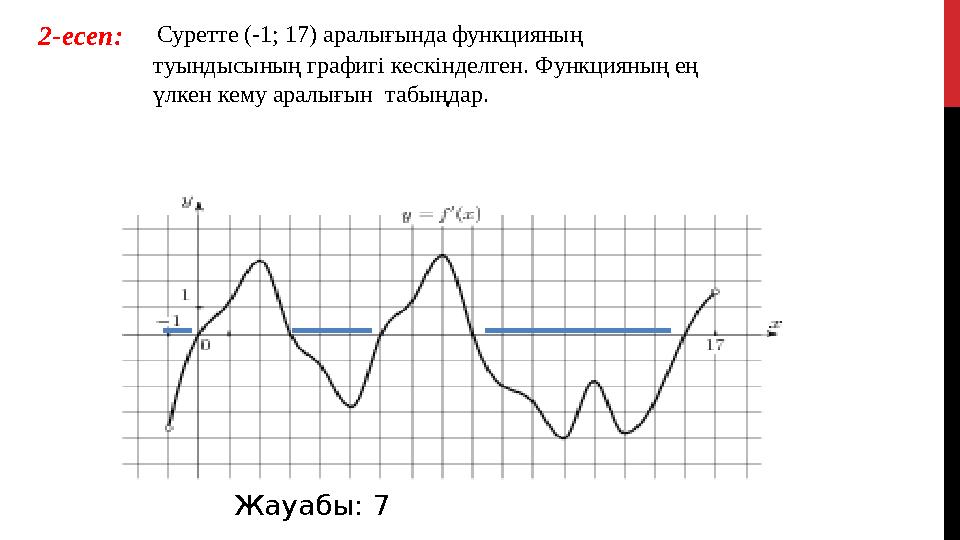
14 слайд
Жауабы: 7 Суретте (-1; 17) аралығында функцияның
туындысының графигі кескінделген. Функцияның ең
үлкен кему аралығын табыңдар. 2-есеп:
14 слайд
Жауабы: 7 Суретте (-1; 17) аралығында функцияның туындысының графигі кескінделген. Функцияның ең үлкен кему аралығын табыңдар. 2-есеп:
15 слайд
Дескрипторлар:
функцияның туындысының графигі арқылы оның
монотонды аралықтарын анықтай алады;
Жауабын қорытындылайды;
15 слайд
Дескрипторлар: функцияның туындысының графигі арқылы оның монотонды аралықтарын анықтай алады; Жауабын қорытындылайды;
16 слайд
ТУЫНДЫ БОЙЫНША ФУНКЦИЯНЫҢ ӨСУ КЕМУ АРАЛЫҒЫН ТАБУ
АЛГОРИТМІ:
1 . Функцияның анықталу облысын табу;
2. Функцияның туындысын табу;
3. f /
(x) > 0 немесе f /
(x) < 0 теңсіздігін шешу;
4. Функцияның өсу және кему аралықтарын
жазу.
16 слайд
ТУЫНДЫ БОЙЫНША ФУНКЦИЯНЫҢ ӨСУ КЕМУ АРАЛЫҒЫН ТАБУ АЛГОРИТМІ: 1 . Функцияның анықталу облысын табу; 2. Функцияның туындысын табу; 3. f / (x) > 0 немесе f / (x) < 0 теңсіздігін шешу; 4. Функцияның өсу және кему аралықтарын жазу.
17 слайд
АЛГОРИТМ БОЙЫНША ШЕШУ ҮЛГІСІ
f(х) = х 4
- 2х 2
функцияның мнотондылығын табыңдар.
1. D(f) = R
2. f /
(x ) = 4 х 3
- 4х,
3. f /
(x)>0, егер 4 х 3
- 4х >0, х 3
- х >0, х(х-1)(х+1)>0
-1 0 1 х f /
(x): - + - +
f(х):
4 . Функция (-∞;-1) ] және [ (0; 1) ] аралығында кемиді.
Функция [ (-1; 0) ] және [ (1; + ∞) ] аралығында өседі.3-есеп.
17 слайд
АЛГОРИТМ БОЙЫНША ШЕШУ ҮЛГІСІ f(х) = х 4 - 2х 2 функцияның мнотондылығын табыңдар. 1. D(f) = R 2. f / (x ) = 4 х 3 - 4х, 3. f / (x)>0, егер 4 х 3 - 4х >0, х 3 - х >0, х(х-1)(х+1)>0 -1 0 1 х f / (x): - + - + f(х): 4 . Функция (-∞;-1) ] және [ (0; 1) ] аралығында кемиді. Функция [ (-1; 0) ] және [ (1; + ∞) ] аралығында өседі.3-есеп.
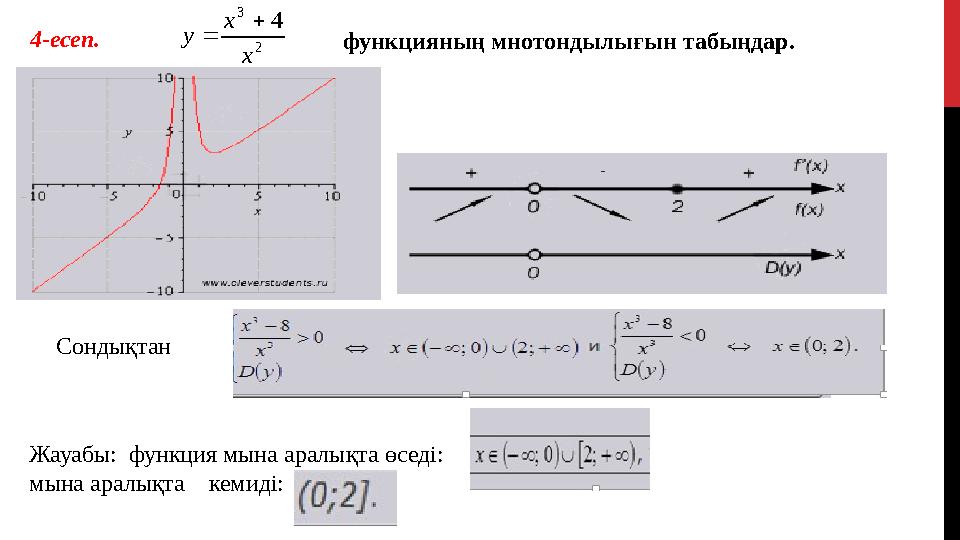
18 слайд
4-есеп.
функцияның мнотондылығын табыңдар.2
3
4
x
x
y
Сондықтан
Жауабы: функция мына аралықта өседі:
мына аралықта кемиді:
18 слайд
4-есеп. функцияның мнотондылығын табыңдар.2 3 4 x x y Сондықтан Жауабы: функция мына аралықта өседі: мына аралықта кемиді:
19 слайд
ЖҰПТЫҚ ЖҰМЫС
Функцияның өсу және кему аралықтарын табыңыздар:; 5 4 2 ) 1
2
х х у
; 2 3 2 1 ) 3 х х у
; 3 2 ) 2 х х у
1 ) 4
2
х х у
19 слайд
ЖҰПТЫҚ ЖҰМЫС Функцияның өсу және кему аралықтарын табыңыздар:; 5 4 2 ) 1 2 х х у ; 2 3 2 1 ) 3 х х у ; 3 2 ) 2 х х у 1 ) 4 2 х х у
20 слайд
Дескрипторлар:
функцияның туындысын табады;
f '(x)>0 немесе f '(x)0 теңсіздігін шешеді;
функцияның өсу (кему) аралықтарын жазады .
20 слайд
Дескрипторлар: функцияның туындысын табады; f '(x)>0 немесе f '(x)0 теңсіздігін шешеді; функцияның өсу (кему) аралықтарын жазады .
21 слайд
Функцияның өсу және кему аралықтарын табыңыздар: Үй жұмысы
21 слайд
Функцияның өсу және кему аралықтарын табыңыздар: Үй жұмысы
22 слайд
22 слайд
