Материалдар / Галилей заңдары

Галилей заңдары

Материал туралы қысқаша түсінік

Механикалық құбылыстарды әр түрлі санақ жүйелерінде қарастыра отырып, Галилей келесі тұжырымғы келді: бірдей бастапқы шарттарда өзара қатысты бір қалыпты қозғалған кез келген инерциялық санақ жүйелерінде барлық механикалық құбылыстар бірдей өтеді. Бұл қағида Галилейлің салыстырмалық принципі деп аталады. Электромагниттік толқындар ашылуына және жарықтың электромагниттік табиғаты анықталуына байланысты электромагниттік құбылыстарға салыстырмалық принципті пайдалану мүмкіншілігі туралы сұрақ туындады.

Айнаш Астаева Ақылбекқызы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

11 Мамыр 2022

631

0 рет жүктелген

Физика Мақала 11 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 18

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Галилейдің салыстырмалылық принципі . Механикадағы салыстырмалы және инвариантты шамалар. Оқытушы: Нугманова Ж.К

1 слайд

Галилейдің салыстырмалылық принципі . Механикадағы салыстырмалы және инвариантты шамалар. Оқытушы: Нугманова Ж.К

2 слайд
 Мақсаты:  Галилейдің салыстырмалы принципі, салыстырмалылық теориясының постулаттары туралы жалпы мағлұмат беру.  Механикадағы салыстырмалы принципі.  Салыстырмалылық теориясының постулаттары. Жарық жылдамдығының шектілігі және ақырғылығын техникада және формулаларын есеп шығаруда қолдана білуге үйрету

2 слайд

 Мақсаты:  Галилейдің салыстырмалы принципі, салыстырмалылық теориясының постулаттары туралы жалпы мағлұмат беру.  Механикадағы салыстырмалы принципі.  Салыстырмалылық теориясының постулаттары. Жарық жылдамдығының шектілігі және ақырғылығын техникада және формулаларын есеп шығаруда қолдана білуге үйрету

3 слайд
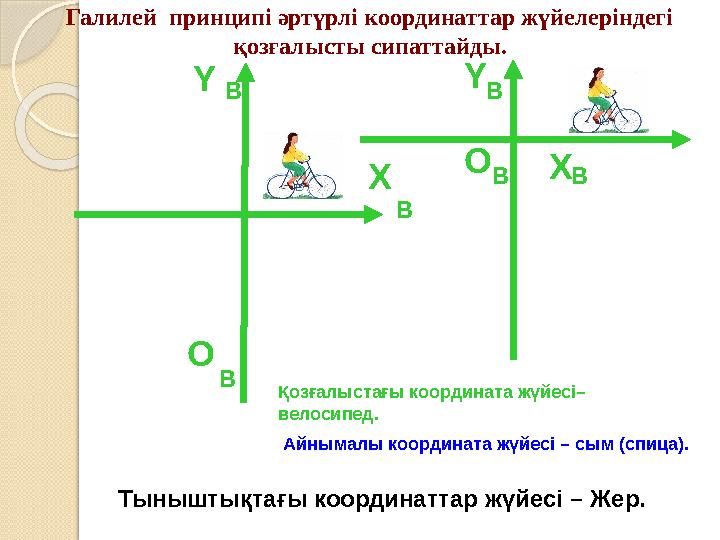
Галилей принципі әртүрлі координаттар жүйелеріндегі қозғалысты сипаттайды. Тыныштықтағы координаттар жүйесі – Жер. O В X ВY B O В X ВY B Қозғалыстағы координата жүйесі– велосипед. Айнымалы координата жүйесі – сым (спица).

3 слайд

Галилей принципі әртүрлі координаттар жүйелеріндегі қозғалысты сипаттайды. Тыныштықтағы координаттар жүйесі – Жер. O В X ВY B O В X ВY B Қозғалыстағы координата жүйесі– велосипед. Айнымалы координата жүйесі – сым (спица).

4 слайд
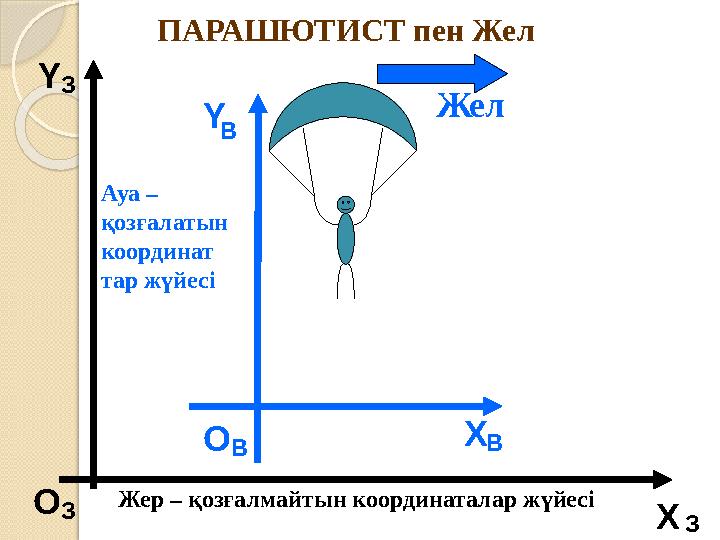
ПАРАШЮТИСТ пен Жел Жер – қозғалмайтын координаталар жүйесі ХY O ЗЗЗ O В X ВY B Жел Ауа – қозғалатын координат тар жүйесі

4 слайд

ПАРАШЮТИСТ пен Жел Жер – қозғалмайтын координаталар жүйесі ХY O ЗЗЗ O В X ВY B Жел Ауа – қозғалатын координат тар жүйесі

5 слайд
 Г. Галилей айтқан – барлық координаталардың инерциялық жүйелеріндегі механикалық құбылыстар біркелкі жүреді деген пайымдау – Галилейдің салыстырмалылық принципі деп аталады.

5 слайд

 Г. Галилей айтқан – барлық координаталардың инерциялық жүйелеріндегі механикалық құбылыстар біркелкі жүреді деген пайымдау – Галилейдің салыстырмалылық принципі деп аталады.

6 слайд
 Галилей түрлендірулері:  Бір санақ жүйесінен екінші санақ жүйесіне көшкенде өзгермей қалатын шамалар инвариантты шамалар деп аталады.  Үдеу-инвариантты (а)

6 слайд

 Галилей түрлендірулері:  Бір санақ жүйесінен екінші санақ жүйесіне көшкенде өзгермей қалатын шамалар инвариантты шамалар деп аталады.  Үдеу-инвариантты (а)

7 слайд
 Салыстырмалылық теориясының постулаттары:  вакуумдегі жарық жылдамдығы жарық көзінің жылдамдығына да жарықты қабылдаушының жылдамдығына да жарықты қабылдаушының жылдамдығына да тәуелсіз. Ол барлық бағытта және барлық инерциялық санақ жүйелерінде бірдей, табиғаттағы ең үлкен шекті жылдамдық.  Кез келген инерциялық жүйеде барлық физикалық құбылыстар бірдей жағдайларда бірдей өтеді, яғни таңдап алынған инерциялық санақ жүйесіне қатысты физикалық заңдар инвариантты .

7 слайд

 Салыстырмалылық теориясының постулаттары:  вакуумдегі жарық жылдамдығы жарық көзінің жылдамдығына да жарықты қабылдаушының жылдамдығына да жарықты қабылдаушының жылдамдығына да тәуелсіз. Ол барлық бағытта және барлық инерциялық санақ жүйелерінде бірдей, табиғаттағы ең үлкен шекті жылдамдық.  Кез келген инерциялық жүйеде барлық физикалық құбылыстар бірдей жағдайларда бірдей өтеді, яғни таңдап алынған инерциялық санақ жүйесіне қатысты физикалық заңдар инвариантты .

8 слайд

9 слайд
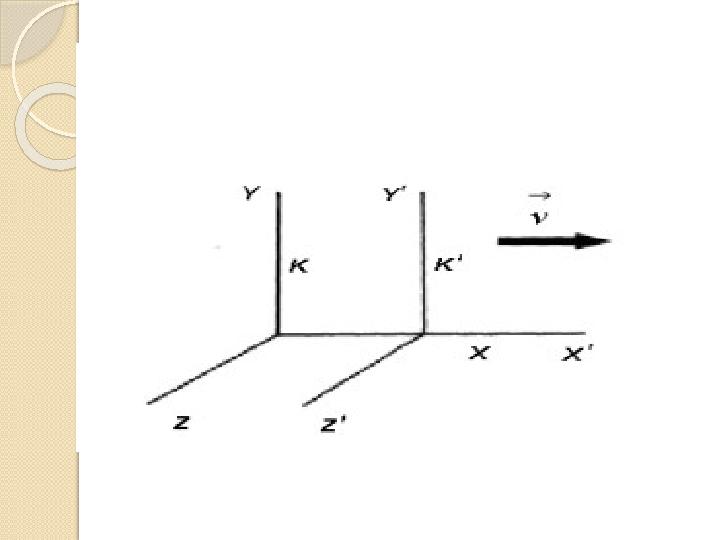
 Қатты дененің ең қарапайым қозғалысы – оның ілгерілемелі бірқалыпты түзу бағыттағы қозғалысы. Осыған сәйкес, санақ жүйелерінің ең қарапайым салыстырмалы түрдегі қозғалысы болып ілгерілемелі бірқалыпты түзу бағыттағы қозғалысы саналады.  Санақ жүйелерінің бірін шартты түрде қозғалмайтын, ал екіншісін – қозғалыста деп алайық.  Әрбір санақ жүйесіне декарттық координаталар жүйесін енгіземіз.  Қозғалмайтын санақ жүйесіндегі К координаталарды ( x, y, z) арқылы, ал қозғалыстағыны K' – (x', y', z') арқылы белгілейік.  Айтайық: " K' координаталар жүйесі К жүйесіне қарасты V жылдамдығымен қозғалуда". Уақыттың әрбір мезетінде қозғалушы координаттар жүйесі қозғалмайтын жүйеге қарасты белгілі бір орында болады.

9 слайд

 Қатты дененің ең қарапайым қозғалысы – оның ілгерілемелі бірқалыпты түзу бағыттағы қозғалысы. Осыған сәйкес, санақ жүйелерінің ең қарапайым салыстырмалы түрдегі қозғалысы болып ілгерілемелі бірқалыпты түзу бағыттағы қозғалысы саналады.  Санақ жүйелерінің бірін шартты түрде қозғалмайтын, ал екіншісін – қозғалыста деп алайық.  Әрбір санақ жүйесіне декарттық координаталар жүйесін енгіземіз.  Қозғалмайтын санақ жүйесіндегі К координаталарды ( x, y, z) арқылы, ал қозғалыстағыны K' – (x', y', z') арқылы белгілейік.  Айтайық: " K' координаталар жүйесі К жүйесіне қарасты V жылдамдығымен қозғалуда". Уақыттың әрбір мезетінде қозғалушы координаттар жүйесі қозғалмайтын жүйеге қарасты белгілі бір орында болады.

10 слайд

11 слайд
 Егер, t=0 мезетінде екі координаталар жүйелерінің де басы сәйкес келген болса, ал t мезетінде қозғалушы координаталар жүйесінің басы қозғалмайтын жүйенің x=vt нүктесінде болады. К жүйесінде қайсыбір Р нүктесінің x, y, z координаталары мен K' жүйесіндегі тура сол нүктенің x', y', z' координаталары арасындағы байланыс мынандай түрге беріледі: x' = x – vt, y' = y, z' = z, t' = t. Бұл формулалар Галилей түрлендірулері деп аталады.

11 слайд

 Егер, t=0 мезетінде екі координаталар жүйелерінің де басы сәйкес келген болса, ал t мезетінде қозғалушы координаталар жүйесінің басы қозғалмайтын жүйенің x=vt нүктесінде болады. К жүйесінде қайсыбір Р нүктесінің x, y, z координаталары мен K' жүйесіндегі тура сол нүктенің x', y', z' координаталары арасындағы байланыс мынандай түрге беріледі: x' = x – vt, y' = y, z' = z, t' = t. Бұл формулалар Галилей түрлендірулері деп аталады.

12 слайд
 Керісінше қозғалмайтын жүйе ретінде K' жүйесін алуға болады. Онда Галилей түрлендірулері мынадай болады:  x = x' + vt', y = y', z = z', t = t'.

12 слайд

 Керісінше қозғалмайтын жүйе ретінде K' жүйесін алуға болады. Онда Галилей түрлендірулері мынадай болады:  x = x' + vt', y = y', z = z', t = t'.

13 слайд
 Түрлендірулердің инварианттары. Координаталардың түрлендірілуі кезінде сандық мәндері өзгермейтін шамалар түрлендірудің инварианттары деп аталады.

13 слайд

 Түрлендірулердің инварианттары. Координаталардың түрлендірілуі кезінде сандық мәндері өзгермейтін шамалар түрлендірудің инварианттары деп аталады.

14 слайд
 Уақыт интервалының инварианттылығы. Уақыт интервалы Галилей түрлендірулерінің инварианты болып табылады

14 слайд

 Уақыт интервалының инварианттылығы. Уақыт интервалы Галилей түрлендірулерінің инварианты болып табылады

15 слайд

16 слайд
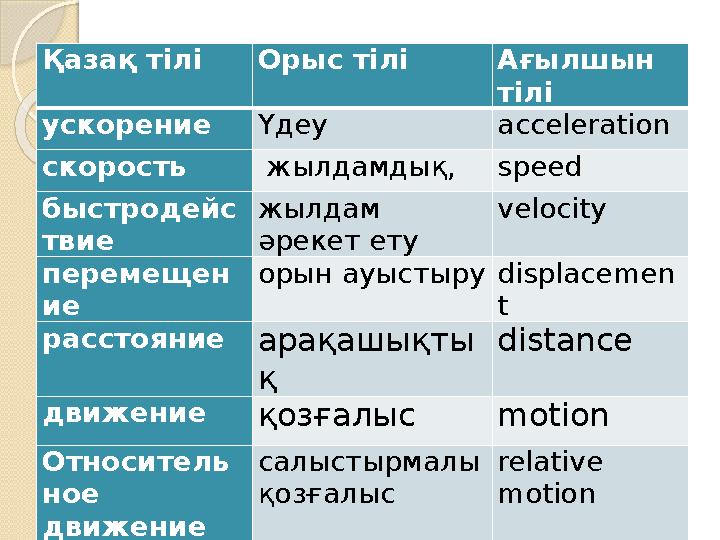
Қазақ тілі Орыс тілі Ағылшын тілі ускорение Үдеу acceleration скорость жылдамдық, speed быстродейс твие жылдам әрекет ету velocity перемещен ие орын ауыстыру displacemen t расстояние арақашықты қ distance движение қозғалыс motion Относитель ное движение салыстырмалы қозғалыс relative motion относительн о салыстырмалы relatively

16 слайд

Қазақ тілі Орыс тілі Ағылшын тілі ускорение Үдеу acceleration скорость жылдамдық, speed быстродейс твие жылдам әрекет ету velocity перемещен ие орын ауыстыру displacemen t расстояние арақашықты қ distance движение қозғалыс motion Относитель ное движение салыстырмалы қозғалыс relative motion относительн о салыстырмалы relatively

17 слайд
Үй жұмысы  Салыстырмалылыққа бір есеп құрастырып келу.

17 слайд

Үй жұмысы  Салыстырмалылыққа бір есеп құрастырып келу.