2024-2025 оқу жылына арналған
қысқа мерзімді сабақ жоспарларын
Жүктеп алғыңыз келеді ме?
ҚР Білім және Ғылым министірлігінің стандартымен жасалған
Иррационал теңсіздік
Материал туралы қысқаша түсінік
Иррационал теңсіздікті шешуде оқушылардың логикасы артады, жай теңсіздік пен иррационал теңсіздігінің айырмасын ажыратады.
Авторы:
28 Желтоқсан 2017
1881
0 рет жүктелген
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 19
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
Иррацион
ал
теңсіздік
1 слайд
Иррацион ал теңсіздік
2 слайд
Сабақтың мақсаты:
Білімділік: Оқушыларды иррационал теңсіздіктерді шешу
әдісімен таныстыру.
Дамытушылық: Жылдам есептеуге дағдыландыру,
логикалық ойлау қабілетін дамыту, теңсіздік түрлерін
пысықтау.
Тәрбиелік: Ұлттық санаға тәрбиелеу, әдептілікке үйрету,
адамдық қасиеттерге баулу.
Сабақтың көрнекілігі: Интерактивті тақта , үлестірмелі
қағаз, сызбалар, деңгейлік тапсырмалар .
Сабақтың түрі: Жаңа сабақ.
Сабақтың әдісі: Жаңа сабақты түсіндіру, білімді
тиянақтау, шығармашылығын дамыту.
2 слайд
Сабақтың мақсаты: Білімділік: Оқушыларды иррационал теңсіздіктерді шешу әдісімен таныстыру. Дамытушылық: Жылдам есептеуге дағдыландыру, логикалық ойлау қабілетін дамыту, теңсіздік түрлерін пысықтау. Тәрбиелік: Ұлттық санаға тәрбиелеу, әдептілікке үйрету, адамдық қасиеттерге баулу. Сабақтың көрнекілігі: Интерактивті тақта , үлестірмелі қағаз, сызбалар, деңгейлік тапсырмалар . Сабақтың түрі: Жаңа сабақ. Сабақтың әдісі: Жаңа сабақты түсіндіру, білімді тиянақтау, шығармашылығын дамыту.
3 слайд
І Жаңа сабақ
Анықтама.
түріндегі теңсіздікті, мұндағы
-иррационал алгебралық функция, иррационал теңсіздік деп атайды,
яғни белгісіз айнымалы түбір таңбасының астында болып келген
теңсіздіктер.
Иррационал теңсіздіктерді әдетте мәндес рационал теңсіздіктер
жүйесіне келтіру әдісімен, жаңа айнымалы ендіру әдісімен, графиктік
әдіспен және теңсіздіктерді шешудің жалпы әдісі мен шығаруға
болады.
Иррационал теңсіздіктерді шешу барысында қате жіберіп алмас
үшін алдымен теңсіздіктің мүмкін мәндерінің облысын яғни анықталу
облысын тауып алу керек.Содан кейін осы анықталу облыста
мәндес теңсіздіктер жүйесіне көше беруге болады.
Иррационал теңсіздіктің шешімін кейбір түрлендірулер арқылы оларды
рационал теңсіздіктер немесе теңсіздіктер жүйесі мәндестігіне
ауыстырады. Бұл түрлендіру қарастырған айнымалыларды ауыстыру және
көбейткіштерге жіктеу және де теңсіздіктің екі жағында бір дәрежеге
шығару болып табылады. Бөгде шешім шықпауын қадағалау керек.[сандық
теңсіздік анықталу облысын, ал облыс мүмкіндігі мәндер шешімі
болады]
3 слайд
І Жаңа сабақ Анықтама. түріндегі теңсіздікті, мұндағы -иррационал алгебралық функция, иррационал теңсіздік деп атайды, яғни белгісіз айнымалы түбір таңбасының астында болып келген теңсіздіктер. Иррационал теңсіздіктерді әдетте мәндес рационал теңсіздіктер жүйесіне келтіру әдісімен, жаңа айнымалы ендіру әдісімен, графиктік әдіспен және теңсіздіктерді шешудің жалпы әдісі мен шығаруға болады. Иррационал теңсіздіктерді шешу барысында қате жіберіп алмас үшін алдымен теңсіздіктің мүмкін мәндерінің облысын яғни анықталу облысын тауып алу керек.Содан кейін осы анықталу облыста мәндес теңсіздіктер жүйесіне көше беруге болады. Иррационал теңсіздіктің шешімін кейбір түрлендірулер арқылы оларды рационал теңсіздіктер немесе теңсіздіктер жүйесі мәндестігіне ауыстырады. Бұл түрлендіру қарастырған айнымалыларды ауыстыру және көбейткіштерге жіктеу және де теңсіздіктің екі жағында бір дәрежеге шығару болып табылады. Бөгде шешім шықпауын қадағалау керек.[сандық теңсіздік анықталу облысын, ал облыс мүмкіндігі мәндер шешімі болады]
4 слайд
Иррационал теңсіздіктерді шешу кезінде мына
төмендегі теоремаларды қолданған тиімді болады.
Теорема.1.1
теңсіздігі
(1)
түріндегі екі рацирнал теңсіздіктер жүйесінің
жиынтығына мәндес.
Теорема.1.2
теңсіздігі
(2)
түріндегі рационал теңсіздіктер жүйесіне мәндес.
4 слайд
Иррационал теңсіздіктерді шешу кезінде мына төмендегі теоремаларды қолданған тиімді болады. Теорема.1.1 теңсіздігі (1) түріндегі екі рацирнал теңсіздіктер жүйесінің жиынтығына мәндес. Теорема.1.2 теңсіздігі (2) түріндегі рационал теңсіздіктер жүйесіне мәндес.
5 слайд
Теорема.1.3
теңсіздігі
(3)
түріндегі рационал теңсіздігіне мәндес.
Теорема.1.4 теңсіздігі
(4)
түріндегі рационал теңсіздігіне мәндес.
Теорема.1.5
теңсіздігі
(5)
тесіздіктер жүйесіне мәндес.
5 слайд
Теорема.1.3 теңсіздігі (3) түріндегі рационал теңсіздігіне мәндес. Теорема.1.4 теңсіздігі (4) түріндегі рационал теңсіздігіне мәндес. Теорема.1.5 теңсіздігі (5) тесіздіктер жүйесіне мәндес.
6 слайд
Теорема.1.6
теңсіздігі
(6)
теңсіздігіне мәндес.
Теорема.1.
7
теңсіздігі
(7)
тесіздіктер жүйесіне мәндес.
Теорема.1.8
теңсіздігі
(8)
теңсіздіктер жүйесіне мәндес.
6 слайд
Теорема.1.6 теңсіздігі (6) теңсіздігіне мәндес. Теорема.1. 7 теңсіздігі (7) тесіздіктер жүйесіне мәндес. Теорема.1.8 теңсіздігі (8) теңсіздіктер жүйесіне мәндес.
7 слайд
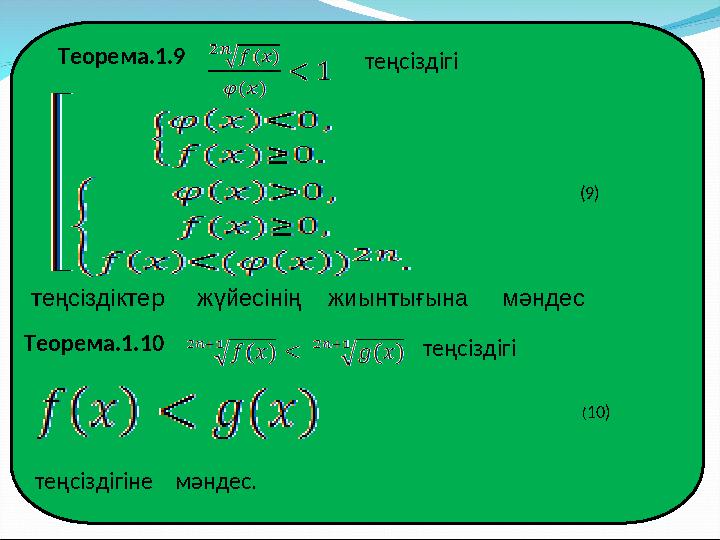
Теорема.1.9
теңсіздігі
(9)
теңсіздіктер жүйесінің жиынтығына мәндес
Теорема.1.10
теңсіздігі
(10)
теңсіздігіне мәндес.
7 слайд
Теорема.1.9 теңсіздігі (9) теңсіздіктер жүйесінің жиынтығына мәндес Теорема.1.10 теңсіздігі (10) теңсіздігіне мәндес.
8 слайд
Теорема.1.11
(11)
Теорема.1.12
(12)
8 слайд
Теорема.1.11 (11) Теорема.1.12 (12)
9 слайд
Мысал.Теңсіздікті шешу.
.
Шешуі:
.
Жауабы:
.
9 слайд
Мысал.Теңсіздікті шешу. . Шешуі: . Жауабы: .
10 слайд
Миға шабуыл
.,
І –топ есептері ІІ-топ есептері
a)Теңсіздіті шешу.a) Теңсіздіті шешу.
b) Теңсіздіті шешу.b) Теңсіздіті шешу.
C) Теңсіздіті шешу.c) Теңсіздіті шешу.
10 слайд
Миға шабуыл ., І –топ есептері ІІ-топ есептері a)Теңсіздіті шешу.a) Теңсіздіті шешу. b) Теңсіздіті шешу.b) Теңсіздіті шешу. C) Теңсіздіті шешу.c) Теңсіздіті шешу.
11 слайд
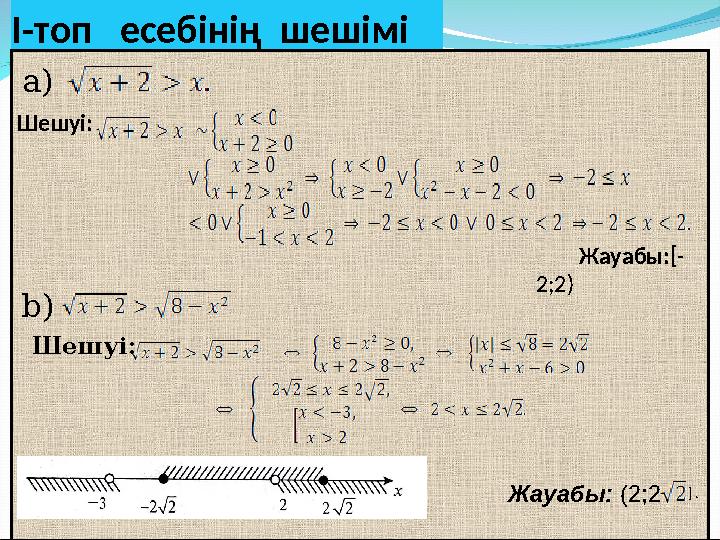
І-топ есебінің шешімі
a)
Шешуі:
Жауабы:[-
2;2)
b)
] .Жауабы: (2;2
Шешуі:
11 слайд
І-топ есебінің шешімі a) Шешуі: Жауабы:[- 2;2) b) ] .Жауабы: (2;2 Шешуі:
12 слайд
C)
Шешуі:
Жауабы:
12 слайд
C) Шешуі: Жауабы:
13 слайд
ІІ-топ есебінің шешімі
a)
Шешуі:
Жауабы: (3;5].
13 слайд
ІІ-топ есебінің шешімі a) Шешуі: Жауабы: (3;5].
![b ) Шешуі: Жауабы: [4;5) (6;7].](https://api.ust.kz/storage/files/materials/ppt/image/2017/december/d28/1514431160-14.jpeg "b ) Шешуі: Жауабы: [4;5) (6;7].")
14 слайд
b
)
Шешуі:
Жауабы:
[4;5)
(6;7].
14 слайд
b ) Шешуі: Жауабы: [4;5) (6;7].
15 слайд
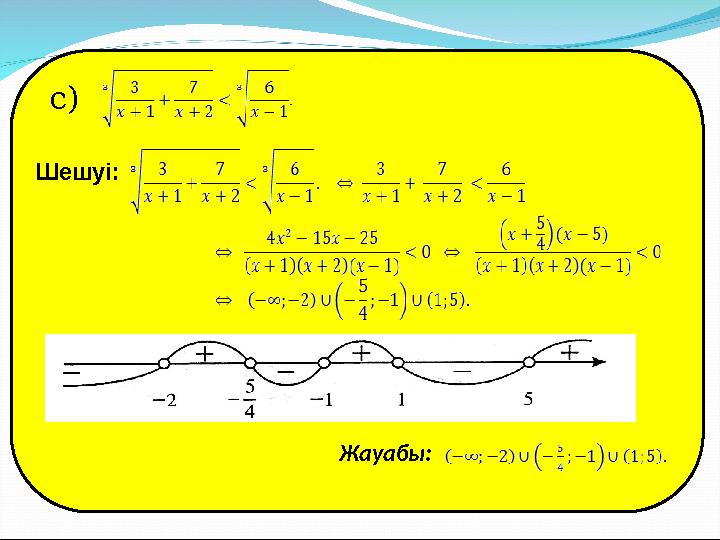
c)
Жауабы:
Шешуі:
15 слайд
c) Жауабы: Шешуі:
16 слайд
Ғажайып үштік
20
30
40
20
30
40
16 слайд
Ғажайып үштік 20 30 40 20 30 40
17 слайд
«20» - Әсем поездың басынан есептегенде 7-вагонға
отырды. Марина поездың соңынан есептегенде 7-вагонға
отырды.Сонда қыздар бір вагонда болады. Поезда неше
вагон болған?
«20»- Сәуледе 6 сақина бар. Оның біреуінің массасы
қалғандарынан ауыр, қалғандарының массалары бірдей.
Табақты таразыға 2 рет қана өлшеп, ауыр сақинаны қалай
анықтауға болады?
«30»- Теңдеуді шешіңіз:
«30»- Теңдеуді шешіңіз:
«40»- Функцияның анықталу облысын тап:
«40»- Функцияның анықталу облысын тап:
17 слайд
«20» - Әсем поездың басынан есептегенде 7-вагонға отырды. Марина поездың соңынан есептегенде 7-вагонға отырды.Сонда қыздар бір вагонда болады. Поезда неше вагон болған? «20»- Сәуледе 6 сақина бар. Оның біреуінің массасы қалғандарынан ауыр, қалғандарының массалары бірдей. Табақты таразыға 2 рет қана өлшеп, ауыр сақинаны қалай анықтауға болады? «30»- Теңдеуді шешіңіз: «30»- Теңдеуді шешіңіз: «40»- Функцияның анықталу облысын тап: «40»- Функцияның анықталу облысын тап:
18 слайд
Сабақты қорытындылау.
Оқушылардың жаңа сабақты
түсінгендігін сұрақтар қою
барысында байқадым.
Үйге тапсырма: 5 есеп.
Оқушыларды бағалау.
18 слайд
Сабақты қорытындылау. Оқушылардың жаңа сабақты түсінгендігін сұрақтар қою барысында байқадым. Үйге тапсырма: 5 есеп. Оқушыларды бағалау.
