Материалдар / Жай бөлшектер

Жай бөлшектер

Материал туралы қысқаша түсінік

5 сынып оқушылары Жай бөлшектер тақырыбын кеңінен түсінуіне көмектеседі.

Бекмахан Айбек Ғабиденұлы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

03 Қазан 2020

453

0 рет жүктелген

Математика Презентация 5 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 22

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Жай бөлшектер Бекмахан Айбек

1 слайд

Жай бөлшектер Бекмахан Айбек

2 слайд
I кезең Ұйымдастыру кезеңі III кезең Жаңа сабақты түсіндіруII кезең “Қызықты сұрақ” әдісі IV кезең “Бағытпен жалғастыр” V кезең “ Сөз тізбегі” әдісі VI кезең “ Есептер әлемі ” ойыны VII кезең ҚорытындылауСабақтың барысы

2 слайд

I кезең Ұйымдастыру кезеңі III кезең Жаңа сабақты түсіндіруII кезең “Қызықты сұрақ” әдісі IV кезең “Бағытпен жалғастыр” V кезең “ Сөз тізбегі” әдісі VI кезең “ Есептер әлемі ” ойыны VII кезең ҚорытындылауСабақтың барысы

3 слайд
1. Натурал сан деген іміз қандай сандар? 2. Жай сан және құрама сан дегеніміз не? 3. ЕҮОБ және ЕКОЕ дегеніміз не?« Қайталау оқу- анасы ». Ауызша сұрақ- жауап алу

3 слайд

1. Натурал сан деген іміз қандай сандар? 2. Жай сан және құрама сан дегеніміз не? 3. ЕҮОБ және ЕКОЕ дегеніміз не?« Қайталау оқу- анасы ». Ауызша сұрақ- жауап алу

4 слайд
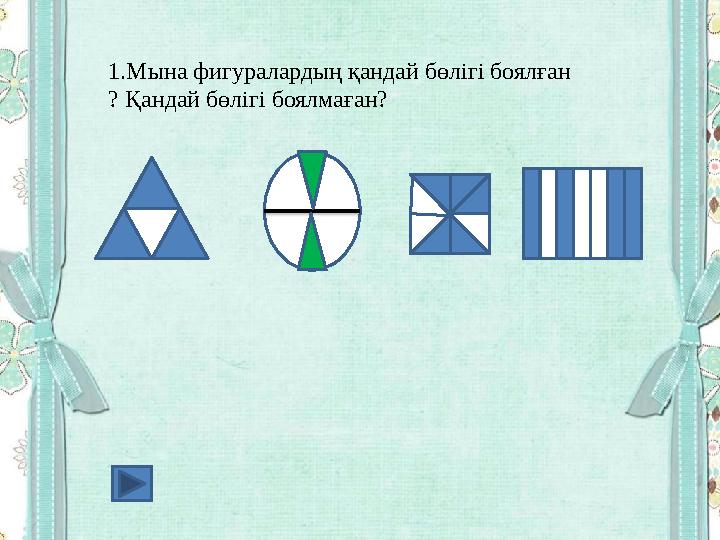
1.Мына фигуралардың қандай бөлігі боялған ? Қандай бөлігі боялмаған?

4 слайд

1.Мына фигуралардың қандай бөлігі боялған ? Қандай бөлігі боялмаған?

5 слайд
2. 1 жылда 365 күн бар.Ақпан айында – 28 күн, ал шілдеде – 31 күн. Ақпан айы жылдың қандай бөлігін құрайды, ал шілде ше?

5 слайд

2. 1 жылда 365 күн бар.Ақпан айында – 28 күн, ал шілдеде – 31 күн. Ақпан айы жылдың қандай бөлігін құрайды, ал шілде ше?

6 слайд
3. Айдар тәуліктің 9 сағатын ұйықтайды, ал сабақты 5 сағат оқиды. Тәуліктің қандай бөлігін ұйықтайды, ал қандай бөлігін сабақ оқиды?

6 слайд

3. Айдар тәуліктің 9 сағатын ұйықтайды, ал сабақты 5 сағат оқиды. Тәуліктің қандай бөлігін ұйықтайды, ал қандай бөлігін сабақ оқиды?

7 слайд
4.Мараттың ұстап алған жыланының ұзындығы 60 см. Жыланның ұзындығы метрдің қандай бөлігін құрайды?

7 слайд

4.Мараттың ұстап алған жыланының ұзындығы 60 см. Жыланның ұзындығы метрдің қандай бөлігін құрайды?

8 слайд
5. 1 алманың салмағы – 200 г. Алма килограмның қандай бөлігін құрайды?

8 слайд

5. 1 алманың салмағы – 200 г. Алма килограмның қандай бөлігін құрайды?

9 слайд
6. Самат 1 сағат серуендеп жүрді. Оның 15 минутын ол көбелек қуды, ал қалған 45 минутын суға шомылды. Сағаттың қандай бөлігін көбелек қуды, ал қандай бөлігін суға шомылды?

9 слайд

6. Самат 1 сағат серуендеп жүрді. Оның 15 минутын ол көбелек қуды, ал қалған 45 минутын суға шомылды. Сағаттың қандай бөлігін көбелек қуды, ал қандай бөлігін суға шомылды?

10 слайд
Ерте кезде адамдарға сауда - саттық және түрлі есептеу жұмыстарында бөлшектер мен үлестерді есептеу қажет болған. Алғашында математикада бөлшектерді «сынық сандар» деп атаған. Бөлшектер туралы түсініктің дамуында үш түрлі бөлшектер ұғымы қалыптасқан: 1. Бірлік бөлшектер (аликвоттық бөлшектер) Алымы бірге тең жай бөлшектер аликвоттық бөлшектер деп аталады.( бірлік бөлшектер деп те аталады). Кез келген аликводтық бөлшек 1 – ден кіші болады. 2. Жүйеленген бөлшектер . Жүйеленген бөлшектер деп – алымы кез келген бүтін сан , бөлімі тек 10 саны немесе 60 саны ғана болатын сан. 3. Жалпы түрдегі бөлшек . Жалпы түрдегі бөлшек – алымы да бөлімі де кез келген сан болады. Бөлшек сызығын – уал – Хассара және италияндық Леонардо Пизанский енгізді.

10 слайд

Ерте кезде адамдарға сауда - саттық және түрлі есептеу жұмыстарында бөлшектер мен үлестерді есептеу қажет болған. Алғашында математикада бөлшектерді «сынық сандар» деп атаған. Бөлшектер туралы түсініктің дамуында үш түрлі бөлшектер ұғымы қалыптасқан: 1. Бірлік бөлшектер (аликвоттық бөлшектер) Алымы бірге тең жай бөлшектер аликвоттық бөлшектер деп аталады.( бірлік бөлшектер деп те аталады). Кез келген аликводтық бөлшек 1 – ден кіші болады. 2. Жүйеленген бөлшектер . Жүйеленген бөлшектер деп – алымы кез келген бүтін сан , бөлімі тек 10 саны немесе 60 саны ғана болатын сан. 3. Жалпы түрдегі бөлшек . Жалпы түрдегі бөлшек – алымы да бөлімі де кез келген сан болады. Бөлшек сызығын – уал – Хассара және италияндық Леонардо Пизанский енгізді.

11 слайд
Бөлшек ұғымының дамуы ғылым мен сауда - саттық жұмыстары өркендеген елдерде: Мысырда, Вавилонда, Үндістанда және Римде қалыптасады. Бөлшек туралы алғашқы түсінік ежелгі Вавилонның ескілікті жазуларында кездеседі. Бөлшекке амалдар қолдану әдісі Мысырдағы Ахмес папирусында (б.з.б. 2000 — 1700 ж.) кездеседі. Бөлшектің осы заманғы белгіленуі ежелгі үнділерде пайда болған. “Бөлшек” термині Еуропаға 1202 жылы арабтардан Леонардо Пизанскийдің еңбегі арқылы енген. Бөлшектің алымы және бөлімі ғылыми атауларын грек монахы, византиялық кезеңнің жалғыз математигі Максим Плануд (1260 - 1310) енгізген.

11 слайд

Бөлшек ұғымының дамуы ғылым мен сауда - саттық жұмыстары өркендеген елдерде: Мысырда, Вавилонда, Үндістанда және Римде қалыптасады. Бөлшек туралы алғашқы түсінік ежелгі Вавилонның ескілікті жазуларында кездеседі. Бөлшекке амалдар қолдану әдісі Мысырдағы Ахмес папирусында (б.з.б. 2000 — 1700 ж.) кездеседі. Бөлшектің осы заманғы белгіленуі ежелгі үнділерде пайда болған. “Бөлшек” термині Еуропаға 1202 жылы арабтардан Леонардо Пизанскийдің еңбегі арқылы енген. Бөлшектің алымы және бөлімі ғылыми атауларын грек монахы, византиялық кезеңнің жалғыз математигі Максим Плануд (1260 - 1310) енгізген.

12 слайд
Жай бөлшектер деп түрінде жазылған сандарды айтамыз, мұндағы m және n – натурал сандар. m саны бөлшектің алымы , ал n саны – оның бөлімі деп аталады. Егер n = 1 болса, онда бөлшек түрінде жазылады және оны көбінесе m деп те белгілейді. Сонымен, дербес жағдайда, кез келген натурал санды бөлімі 1- ге тең жай бөлшек түрінде көрсетуге болады.n m 1 m

12 слайд

Жай бөлшектер деп түрінде жазылған сандарды айтамыз, мұндағы m және n – натурал сандар. m саны бөлшектің алымы , ал n саны – оның бөлімі деп аталады. Егер n = 1 болса, онда бөлшек түрінде жазылады және оны көбінесе m деп те белгілейді. Сонымен, дербес жағдайда, кез келген натурал санды бөлімі 1- ге тең жай бөлшек түрінде көрсетуге болады.n m 1 m

13 слайд
Бөлшектің алымы бөлімінен кіші болса, бұндай бөлшек дұрыс бөлшек деп аталады. Мысалы, бөлшегі дұрыс бөлшек болады, себебі 2 < 7. Бөлшектің алымы бөлімінен үлкен болса, бұндай бөлшек бұрыс бөлшек деп аталады. Мысалы, бөлшегі бұрыс бөлшек болады, себебі 8 > 3.Дұрыс және бұрыс бөлшектер7 2 3 8

13 слайд

Бөлшектің алымы бөлімінен кіші болса, бұндай бөлшек дұрыс бөлшек деп аталады. Мысалы, бөлшегі дұрыс бөлшек болады, себебі 2 < 7. Бөлшектің алымы бөлімінен үлкен болса, бұндай бөлшек бұрыс бөлшек деп аталады. Мысалы, бөлшегі бұрыс бөлшек болады, себебі 8 > 3.Дұрыс және бұрыс бөлшектер7 2 3 8

14 слайд
Аралас бөлшек Оң санның және дұрыс бөлшектің қосындысы аралас б өлшек деп аталады. Бұны былай жазады:2 1 1 2 1 1  

14 слайд

Аралас бөлшек Оң санның және дұрыс бөлшектің қосындысы аралас б өлшек деп аталады. Бұны былай жазады:2 1 1 2 1 1  

15 слайд
Егер ad=bc орындалса, онда және екі бөлшек тең деп саналады. Мысалы, және бөлшектері тең болып табылады, себебі b a d c 7 4 21 12 12 7 21 4    Егер бөлшектің алымы мен бөлімін бірдей шамаға көбейтсе: , бөлшектер әртүрлі болғанымен бөлшектің мәні өзгермейді. Бұл қасиет бөлшектің негізгі қасиеті деп аталады. Мысалы, c b c a b a    12 16 3 4 

15 слайд

Егер ad=bc орындалса, онда және екі бөлшек тең деп саналады. Мысалы, және бөлшектері тең болып табылады, себебі b a d c 7 4 21 12 12 7 21 4    Егер бөлшектің алымы мен бөлімін бірдей шамаға көбейтсе: , бөлшектер әртүрлі болғанымен бөлшектің мәні өзгермейді. Бұл қасиет бөлшектің негізгі қасиеті деп аталады. Мысалы, c b c a b a    12 16 3 4 

16 слайд
Егер бөлшектің алымы мен бөлімінің бірдей көбейткіштері болса, оны алып тастауға болады. Бұл операция бөлшекті қысқарту деп аталады. Мысалы, Егер бөлшектің алымы мен бөлімі өзара жай сандар болса, онда бөлшек қысқартылмайды делінеді. Мысалы, қысқартылмайтын бөлшек, себебі 25 және 14 сандары өзара жай.14 25 9 4 36 16 

16 слайд

Егер бөлшектің алымы мен бөлімінің бірдей көбейткіштері болса, оны алып тастауға болады. Бұл операция бөлшекті қысқарту деп аталады. Мысалы, Егер бөлшектің алымы мен бөлімі өзара жай сандар болса, онда бөлшек қысқартылмайды делінеді. Мысалы, қысқартылмайтын бөлшек, себебі 25 және 14 сандары өзара жай.14 25 9 4 36 16 

17 слайд
Бірлік кесіндісі берілген сәуле координата- лық сәуле деп аталады. Бөлшекті координаталық сәуледе кескіндеу үшін : 1. бөлшектің бөлімінде қандай сан болса, бірлік кесінді сонша тең бөлікке бөлінеді. 2. бөлшектің алымында қандай сан болса, бірлік кесіндінің сонша бөлігін алу керек.  Дұрыс бөлшек 1 – ден кіші болғандықтан, ол координаталық сәуледе 0- ден 1- ге дейінгі аралықтағы нүктелермен кескінделеді.  Бұрыс бөлшек 1-ге тең немесе 1- ден үлкен болғандықтан, координаталық сәуледе 1-де немесе 1- дің оң жағында кескінделеді.

17 слайд

Бірлік кесіндісі берілген сәуле координата- лық сәуле деп аталады. Бөлшекті координаталық сәуледе кескіндеу үшін : 1. бөлшектің бөлімінде қандай сан болса, бірлік кесінді сонша тең бөлікке бөлінеді. 2. бөлшектің алымында қандай сан болса, бірлік кесіндінің сонша бөлігін алу керек.  Дұрыс бөлшек 1 – ден кіші болғандықтан, ол координаталық сәуледе 0- ден 1- ге дейінгі аралықтағы нүктелермен кескінделеді.  Бұрыс бөлшек 1-ге тең немесе 1- ден үлкен болғандықтан, координаталық сәуледе 1-де немесе 1- дің оң жағында кескінделеді.

18 слайд
 Координаталық сәуле бойында берілген нүкте бір ғана санға сәйкес келеді  Жай бөлшек пен аралас сандардың координаталық сәуледегі орнын белгілеу үшін, бірлік кесіндінің ұзындығын дұрыс таңдау маңызды.  Жай бөлшектерді координаталық сәуледе белгілеудің ең қолайлы нұсқасы — бірлік кесіндіні бөлшектің бөліміндегі сандарға сәйкес тор көздермен алу керек. Мысалы, егер, сандарын координаталық сәуледе белгілеу берілсе, онда бірлік кесіндінің ұзындығын 5 тор көзден тұратындай етіп алған жөн.

18 слайд

 Координаталық сәуле бойында берілген нүкте бір ғана санға сәйкес келеді  Жай бөлшек пен аралас сандардың координаталық сәуледегі орнын белгілеу үшін, бірлік кесіндінің ұзындығын дұрыс таңдау маңызды.  Жай бөлшектерді координаталық сәуледе белгілеудің ең қолайлы нұсқасы — бірлік кесіндіні бөлшектің бөліміндегі сандарға сәйкес тор көздермен алу керек. Мысалы, егер, сандарын координаталық сәуледе белгілеу берілсе, онда бірлік кесіндінің ұзындығын 5 тор көзден тұратындай етіп алған жөн.

19 слайд
Егер бөлшек әр түрлі бөлімде берілсе, онда координаталық сәуленің бірлік кесіндісін мүмкіндігінше барлық бөлшектердің ортақ бөлімдеріне сәйкес келетін тор көздермен алған жөн. Мысалы, егер бөлшектердің бөлімдері 8, 4 және 2 болса, онда бірлік кесінді ұзындығын сегіз тор көз етіп алған ыңғайлы. санын координаталық сәуледе белгілеу қажет болса, бірлік кесіндіні 8 бөлікке бөліп, соның 7 бөлігін аламыз.8 7

19 слайд

Егер бөлшек әр түрлі бөлімде берілсе, онда координаталық сәуленің бірлік кесіндісін мүмкіндігінше барлық бөлшектердің ортақ бөлімдеріне сәйкес келетін тор көздермен алған жөн. Мысалы, егер бөлшектердің бөлімдері 8, 4 және 2 болса, онда бірлік кесінді ұзындығын сегіз тор көз етіп алған ыңғайлы. санын координаталық сәуледе белгілеу қажет болса, бірлік кесіндіні 8 бөлікке бөліп, соның 7 бөлігін аламыз.8 7

20 слайд
Тапсырманы орындау алгоритмі: 1. Ох сәулесін сол жақтан оң жаққа қарай сызыңдар; 2. Ох сәулесінің бас нүктесі – О нүктесіне 0 санын сәйкестендіріп, О нүктесін санақ басы етіп алыңдар. 3. Ох сәулесінің бойынан ұзындығы 5 см кесіндіні алып, кесіндінің ұшына 1 санын сәйкестендіріп, А нүктесімен белгілеңдер. (ОА бірлік кесінді) 4. Сәуленің санақ басынан (О – нүктесінен) бастап жалғастыра екі бірлік кесіндіні салып, 2 санын сәйкестендіріп, В нүктесін жазыңдар. 5. Сәуленің бойында 3 санын кескіндеу үшін, сәуленің санақ басынан (О – нүктесінен) бастап жалғастыра үш бірлік кесіндіні салып, оның ұшын С нүктесімен белгілеңдер. (Осылайша жалғастырғанда координаталық сәуле сызылады.Координаталық сәуледегі берілген нүктеге сәйкес келетін сан, осы нүктенің координасы деп аталады.) 6. Сонан соң осы кесіндінің бойынан бөлшектерін кескіндеп , оны әріптермен белгілеңдер.

20 слайд

Тапсырманы орындау алгоритмі: 1. Ох сәулесін сол жақтан оң жаққа қарай сызыңдар; 2. Ох сәулесінің бас нүктесі – О нүктесіне 0 санын сәйкестендіріп, О нүктесін санақ басы етіп алыңдар. 3. Ох сәулесінің бойынан ұзындығы 5 см кесіндіні алып, кесіндінің ұшына 1 санын сәйкестендіріп, А нүктесімен белгілеңдер. (ОА бірлік кесінді) 4. Сәуленің санақ басынан (О – нүктесінен) бастап жалғастыра екі бірлік кесіндіні салып, 2 санын сәйкестендіріп, В нүктесін жазыңдар. 5. Сәуленің бойында 3 санын кескіндеу үшін, сәуленің санақ басынан (О – нүктесінен) бастап жалғастыра үш бірлік кесіндіні салып, оның ұшын С нүктесімен белгілеңдер. (Осылайша жалғастырғанда координаталық сәуле сызылады.Координаталық сәуледегі берілген нүктеге сәйкес келетін сан, осы нүктенің координасы деп аталады.) 6. Сонан соң осы кесіндінің бойынан бөлшектерін кескіндеп , оны әріптермен белгілеңдер.

21 слайд
Назарларыңызға рахмет!!!

21 слайд

Назарларыңызға рахмет!!!