Жиын және оның элементтері
Материал туралы қысқаша түсінік
жиындар тақырыбына дайын материал
Авторы:
03 Маусым 2018
1478
2 рет жүктелген
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 14
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
ЖИЫН ЖӘНЕ ОНЫҢ
ЭЛЕМЕНТТЕРІ
Сынып жұмысы 10.10.2012 ж
1 слайд
ЖИЫН ЖӘНЕ ОНЫҢ ЭЛЕМЕНТТЕРІ Сынып жұмысы 10.10.2012 ж
2 слайд
Жиын
2 слайд
Жиын
3 слайд
Элементтері
Жиын -
Элементтері –
А={}
Анықтама
3 слайд
Элементтері Жиын - Элементтері – А={} Анықтама
4 слайд
Бос жиын Ø.
4 слайд
Бос жиын Ø.
5 слайд
Жиын :
Шектеусіз жиынШектеулі жиын
5 слайд
Жиын : Шектеусіз жиынШектеулі жиын
6 слайд
Тең жиындар
6 слайд
Тең жиындар
7 слайд
Жиындарға мінездеме беру
1. А = { дүйсенбі, сейсенбі, сәрсенбі,
бейсенбі, жұма, сенбі, Жексенбі}
Жауабы: апта күндерінің жиыны.
7 слайд
Жиындарға мінездеме беру 1. А = { дүйсенбі, сейсенбі, сәрсенбі, бейсенбі, жұма, сенбі, Жексенбі} Жауабы: апта күндерінің жиыны.
8 слайд
Егер В жиынының әрбір элементі а жиынына да
тиісті болса, онда В жиыны А жиынының ішкі
жиыны деп аталады.
В ϲ А ( ϲ – тиісті белгісі)
оқылуы:
В- жиыны А жиынының ішкі жиыны;
Мысалы, A={1,2,3,4,5,6,7} жиынындағы жұп сандар
жиыны – B={2,4,6}.
B жиынының әрбір элементі A жиынына тиісті.
Белгіленуі: B Є A. Оқылуы: B жиыны – A
жиынының ішкі жиыны.
8 слайд
Егер В жиынының әрбір элементі а жиынына да тиісті болса, онда В жиыны А жиынының ішкі жиыны деп аталады. В ϲ А ( ϲ – тиісті белгісі) оқылуы: В- жиыны А жиынының ішкі жиыны; Мысалы, A={1,2,3,4,5,6,7} жиынындағы жұп сандар жиыны – B={2,4,6}. B жиынының әрбір элементі A жиынына тиісті. Белгіленуі: B Є A. Оқылуы: B жиыны – A жиынының ішкі жиыны.
9 слайд
А
B
Жиындардың байланыстары мен арақатынастары
Эйлер-Венн дөңгелектері арқылы кескінделеді.
Венн- ағылшын математигі (xxғ)
Эйлер- (1707-1783ж.) швейцариялық математик ,
Эйлер – Венн дөңгелектері
B жиыны A жиынының ішкі жиыны
Бос жиын кез келген жиынның ішкі жиыны болады.
Белгіленуі: Ø Є A. Мұндағы A - қандай да бір жиын.
9 слайд
А B Жиындардың байланыстары мен арақатынастары Эйлер-Венн дөңгелектері арқылы кескінделеді. Венн- ағылшын математигі (xxғ) Эйлер- (1707-1783ж.) швейцариялық математик , Эйлер – Венн дөңгелектері B жиыны A жиынының ішкі жиыны Бос жиын кез келген жиынның ішкі жиыны болады. Белгіленуі: Ø Є A. Мұндағы A - қандай да бір жиын.
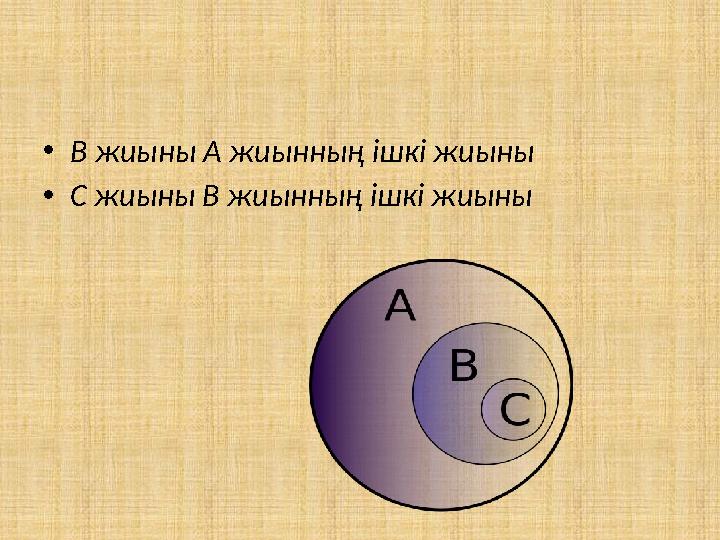
10 слайд
•В жиыны А жиынның ішкі жиыны
•С жиыны В жиынның ішкі жиыны
10 слайд
•В жиыны А жиынның ішкі жиыны •С жиыны В жиынның ішкі жиыны
11 слайд
Жиындардың қиылысуы. Жиындардың
бірігуі.
Екі жиынның қиылысуы деп сол екі
жиынның екеуіне де тиісті элементтерден
ғана тұратын жиынды атайды.
С={4,7,9,13} D={2,10,7,6,13} онда
С ∩ D ={7,13}
11 слайд
Жиындардың қиылысуы. Жиындардың бірігуі. Екі жиынның қиылысуы деп сол екі жиынның екеуіне де тиісті элементтерден ғана тұратын жиынды атайды. С={4,7,9,13} D={2,10,7,6,13} онда С ∩ D ={7,13}
12 слайд
Егер екі жиындардың ортақ элементтері
болмаса, онда олардың қиылысуы бос жиын
болады. .
А ∩ В =ᴓ
12 слайд
Егер екі жиындардың ортақ элементтері болмаса, онда олардың қиылысуы бос жиын болады. . А ∩ В =ᴓ
13 слайд
Екі жиынның бірігуі деп әрбір элементі сол
екі жиынның кем дегенде біреуіне тиісті
болатын жиынды атайды.
N={a,b,c,d,e} P={d,e,x,y} онда
N U P ={a,b,c,d,e,x,y}
N U P
13 слайд
Екі жиынның бірігуі деп әрбір элементі сол екі жиынның кем дегенде біреуіне тиісті болатын жиынды атайды. N={a,b,c,d,e} P={d,e,x,y} онда N U P ={a,b,c,d,e,x,y} N U P
