Кеплер заңдары

1 слайд
Кеплер заңдары

1 слайд

2 слайд
Иоганн Кеплер өмірбаяны  ( . Кеплер Иоганн нем Johannes Kepler 27.12. 1571, , , - - . – Германия Вюртемберг Вейль дер Штадт қ 15.11.1630, , .) - Бавария Регенсбург қ Нем i , с астрономы . математигі Х V . - ІІ ғ адамзаттық ғылым техника . төңкерісінің дәуір бөлгіш тұлғаларының бірі Әйгілі астроном Тихо Брагенің қол астында зерттеумен . айналысқан шәкірті Тихо Браге көптеген астрономиялық құбылыстарды көзеткенімен оларға . синтез жасай алмады Ал Кеплер болса оларды , , . қорытып анализдеп әйгілі заңдарды туғызды Ол әйгілі планеталар қозғалысына қатысты Кеплер . " ", заңдарын ашты Кейінгілер оның жаңа астрономия " ", Әлемнің гармониясы Коперниг астрономиясы " туралы кітаптары арқылы планеталар . қозғалысының үш заңын тұрақтандырды Ол өзінен кейінгі Ньютон секілді ғалымдардың бүкіл әлемдік . тартылыс заңын ашуына тікелей ықпал етті

2 слайд

3 слайд
 1593 . i i i i. 1594-1600 . . Иоганн Кеплер ж Тюбиген университет н б т ред ж ж Грацтег i жоғарғы мектепте жұмыс i стейд i. 1600 . ж Прагаға астроном Тихо Брагеге көш i п кетед i, 1612 . . ал ж Линцке қоныс аударады Кеплерд i ң зерттеулер i , астрономия , . механика оптика және математика салаларына байланысты болады Тихо Браген i ң және өз i н i , ң бақылауларын пайдаланып планеталардың қозғалыс заңдарын ашты ( Кеплерд i 3 ). ң заңы  ,  Ескі қаладағы Карлова көшесіндегі Иоганн Кеплер тұрған үй Прага  Кеплерд i ң оптикаға енг i зген жем i с i . 1604 . " " мол ж шыққан Вителлияға қосымша трактатында жаңа оптиканың нег i з i және көру механизм i бер i . лген  1604 . ж жарықтандыру және жарық көз i не дей i нг i ара қашықтық квадратының арасындағы байланыстың кер i . пропорционалзаңын ашты  Кеплер телескоп құрастырушы рет i нде белг i л i , , оның трактаттарында сонымен қатар , шағылу заңы толық i шк i , бейнелеу құбылысы линза формуласы және көру шарты . сипатталған

3 слайд

4 слайд
Ғылым жолына алғаш қадам басқан жылдары  Алғаш Кеплер протестант уағыздаушысы , болғысы келді бірақ оның матиматикалық , 1594 . қабілеттілігінің арқасында Кеплерді ж ( ) Граца қазіргі Австрия университетіне дәріс . 6 оқуға шақырады Граца Кеплер жыл өмір . « сүреді Осында оның алғаш кітабы Әлемнің » (1596) . « құпия сыры шығады Әлемнің құпия » сыры кітабын Кеплер Галилеоға және Тихо . Брагаға жіберді Мистикалық , нумерологияны қостамағандығыменнен Галилей Кеплерд i ң гелиоорталық жолын . мақұлдады Ал Тихо Браге Кеплерді өзіне . шақырады Кеплер католиктердің қудалауы . салдарынан Грацтан кетуге мәжбүр болған

4 слайд

5 слайд
Кеплер заңдарыКеплер заңдары  – 17 - Кеплер заңдары ғ дың басында Иоганн Кеплер ашқан планеталар . қозғалысының үш заңы “ Кеплердің Жаңа ” (1609) астрономия атты негізгі еңбегінде алғашқы . екі заң баяндалған Үшінші заң кейінірек “ ашылған және ол Әлем ” (1619) 5- гармониясы атты 3- кітабының тарауында . берілген

5 слайд

6 слайд
Кеплердің бірінші заңы  ( ) Ұйтқымаған қозғалысқа яғни екі дене есебінде қатынасатын нүктенің орбитасы екінші ретті қисық сызықпен өрнектеледі және оның бір . фокусында тарту күшінің центрі орналасады Сонымен ұйытқымаған қозғалыстағы материалдық нүктенің орбитасы конустық , , қималардың бірі яғни шеңбер эллипс ( ), планеталар үшін парабола не гипербола . түрінде болады Кеплердің бірінші заңы негізінен планета орбитасының пішінін : анықтайды Барлық планеталар Күнді эллипс , бойымен айналады оның фокустарының бірінде . Күн орналасады  – , Эллипстің симметриялы центрі О үлкен 1=2 1=2 , АА а және ВВ в екі симметрия осі бар – , – мұндағы а үлкен жарты ось в кіші жарты ось . деп аталады

6 слайд

7 слайд
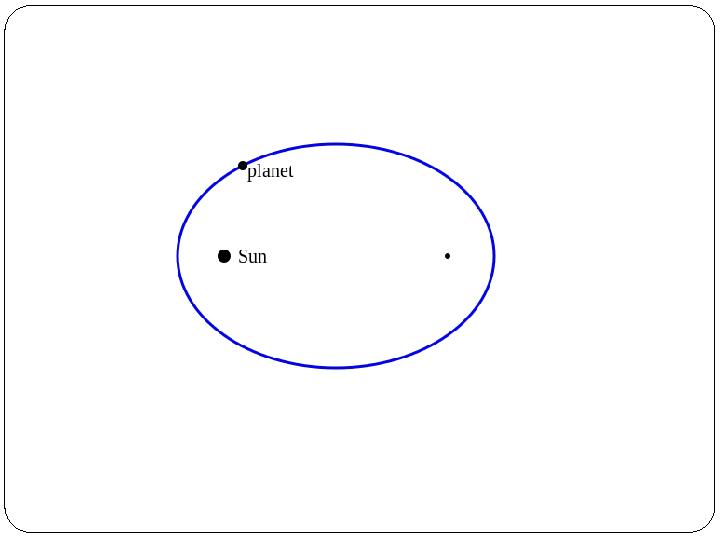
Әрбір планета Күнді эллипстік орбита бойымен айналып жүреді және оның фокустарының бірінде Күн тұрады.

7 слайд

8 слайд
ЭЛИППСТІҢ НЕГІЗГІ ҚАСИЕТТЕРІ. ЭЛЛИПС ДЕГЕНІМІЗ – БЕРІЛГЕН ЕКІ Ғ 1 , Ғ 2 НҮКТЕЛЕРДЕН ҚАШЫҚТАРЫНЫҢ ҚОСЫНДЫСЫ ТҰРАҚТЫ БОЛЫП ҚАЛАТЫН НҮКТЕЛЕРДІҢ ГЕОМЕТРИЯЛЫҚ ОРНЫ. МҒ 1 +МҒ 2 =2а – эллипстің үлкен осінің ұзындығы. А – эллипстің үлкен жарты осі. │ Ғ 1 Ғ 2 │=2с фокустардың ара қашықтығы фокус аралығы деп аталады. ВD=2b кесіндісі – эллипстің кіші осі. ε=2с/2а немесе ε=с/а – эллипстің эксцентриситеті.

8 слайд

9 слайд

9 слайд

10 слайд
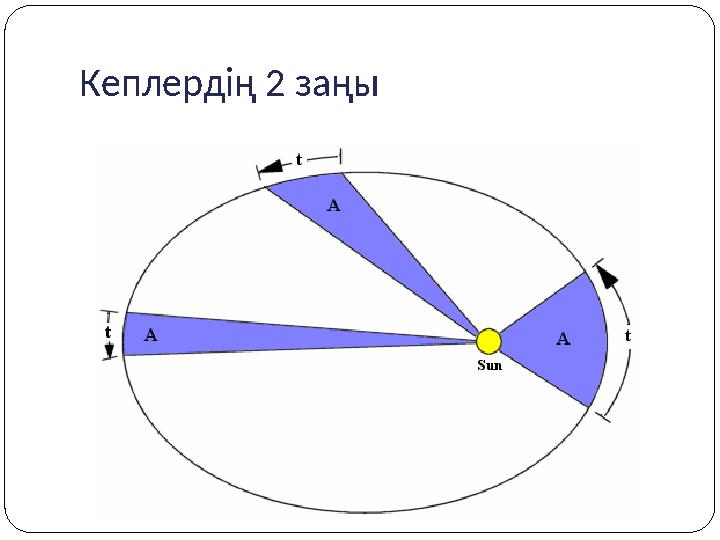
Кеплердің екінші заңы Күнді планетамен жалғастырып тұратын түзу, бірдей уақыт аралығында бірдей аудандарды қамтып өтеді.

10 слайд

11 слайд
Кеплердің 2 заңы

11 слайд

12 слайд
Кеплердің үшінші заңы Барлық планеталар үшін эллипстің үлкен жарты осі кубының планетаның Күнді айналу периодының квадратына қатынасы бірдей болады:

12 слайд