Комбинаторика және ықтималдық теориясы
Комбинаторика және ықтималдық теориясы


#1 слайд
Комбинаторика
және
ықтималдық теориясы
Өтеш Ақжүніс
Қарағанды қаласы, №34 ЖББОМ
9 «б» сынып о қушысы Өтеш Ақжүніс
Жетекшісі:Пирназарова А.Б
1 слайд
Комбинаторика және ықтималдық теориясы Өтеш Ақжүніс Қарағанды қаласы, №34 ЖББОМ 9 «б» сынып о қушысы Өтеш Ақжүніс Жетекшісі:Пирназарова А.Б

#2 слайд
Басты ма қсатым :
Басты м індетім : Техника мен білімді одан әрмен жоғары
қарай дамыту. Комбинаторика мен
ықтималдық теорияны кеңінен түсіндіру.
Түрлі салаларда статистикалық бақылау
үшін математикалық мақсат құру.
Оқушылар көзқарасын, білімін кеңейту.
Комбинаторика және ықтималдық
теориясының формулаларын пайдалану,
кеңінен қарастыру жәнеде мәнін ашу. Түрлі
салаларда, өмірде кездесетін кездейсоқ
оқиғаларда, есептеулерде қолдану.
2 слайд
Басты ма қсатым : Басты м індетім : Техника мен білімді одан әрмен жоғары қарай дамыту. Комбинаторика мен ықтималдық теорияны кеңінен түсіндіру. Түрлі салаларда статистикалық бақылау үшін математикалық мақсат құру. Оқушылар көзқарасын, білімін кеңейту. Комбинаторика және ықтималдық теориясының формулаларын пайдалану, кеңінен қарастыру жәнеде мәнін ашу. Түрлі салаларда, өмірде кездесетін кездейсоқ оқиғаларда, есептеулерде қолдану.

#3 слайд
Комбинаторика және ықтималдық
теориясы дегеніміз не?
Комбинаторика – бұл әртүрлі жиынтығы бар
элементтер санының саналу жолдарын зерттейді.
Латын тілінен аударғанда “combino”
“жалғастыру” деген мағына береді.
Ықтималдық теориясы дегеніміз – кездейсоқ
проблемалардың математикалық үлгісі.
Комбинаториялық әдістер және ықтималдық
теориясы статистика, эконмика, физика, химия,
биология сияқты ғылымдарда қолданылады.
Жауабы нешеу? Неше әдіспен? Мүмкіндігі
қанша? Міне осы сияқты сұрақтардың жауабын
математикалық тұрғыда дәлелдейді.
3 слайд
Комбинаторика және ықтималдық теориясы дегеніміз не? Комбинаторика – бұл әртүрлі жиынтығы бар элементтер санының саналу жолдарын зерттейді. Латын тілінен аударғанда “combino” “жалғастыру” деген мағына береді. Ықтималдық теориясы дегеніміз – кездейсоқ проблемалардың математикалық үлгісі. Комбинаториялық әдістер және ықтималдық теориясы статистика, эконмика, физика, химия, биология сияқты ғылымдарда қолданылады. Жауабы нешеу? Неше әдіспен? Мүмкіндігі қанша? Міне осы сияқты сұрақтардың жауабын математикалық тұрғыда дәлелдейді.

#4 слайд
ТарихКомбинаторика
Комбинаторика, комбинаторикалық талдау ұғымы алғаш 1666 жылы
Лейнбистің «Комбинаторлық өнерге арналған дискурстар» атты еңбегінде
жарыққа шыққан. Комбинаторлық ұғымдар мен санақ нәтижелері ежелден
пайда болды. Б.з.д. 6 ғасырда ежелгі үнді дәрігері Сушрута Самхита 63
түрлі дәріні 6 түрлі дәмнен жасауға болатындығын, ал бір уақытта екі рет,
екеуін де бір уақытта қабылдайтынын және осылайша 26-дан 1 мүмкіндікті
есептеп шығаруға шақырды. Паскаль, Ньютон, Джейкоб Бернулли және
Эйлердің туындылары жаңадан пайда болған салаға негіз болды. Граф
теориясы, сонымен бірге, төрт түсті мәселеге байланысты қызығушылықтың
жарылысына ие болды. Джероламо Кардоно өлімінен кейін жазылған
дисктерде математикалық зерттеулер туралы жазған. Бұл ойын теориясы
деседе болады. Ойын теориясына Тарталия мен Галилей қатысты. Шетелдік
ойыншы Чевалиер де Мерет пен Перре Фермат және Блейз Паскаль, онда
бірнеше күрделі комбинаторлық сұрақтар туындаған кездегі сәйкестікті
ықтималдықтар теориясы тарихына енгізді. Құмар ойындардан басқа,
шифрларды жасау және оларды бұзу үшін де криптографияда
комбинаторлық әдістер қолданылды. Міне осылайша комбинаторикалық
ұғым пайда болды.
Ықтималдық
Кристиан Гюйгенс ықтималдық туралы алғашқы кітабын
жариялады.Ричард Джеффридің айтуынша, « XVII ғасырдың ортасына дейін«
ықтимал »термині мақұлданды және бұл мағынада бірден көзқарас пен іс-
қимылға қолданылды. Алайда, заң тұрғысынан, әсіресе, ықтимал,
дәлелдемелер бар ұсыныстарды қолдануға болады . Ықтималдық құмар
ойын әсерінен туындаған. Құмар ойын барысында ойыншыларды
толғандырған сұрақтар ықтималдық теориясын қалыптастырды. Тарих
Комбинаторика
Комбинаторика, комбинаторикалық талдау ұғымы алғаш 1666 жылы Лейнбистің
«Комбинаторлық өнерге арналған дискурстар» атты еңбегінде жарыққа шыққан.
Б.з.д. 6 ғасырда ежелгі үнді дәрігері Сушрута Самхита 63 түрлі дәріні 6 түрлі
дәмнен жасауға болатындығын есептеп шығаруға шақырды. Паскаль, Ньютон,
Джейкоб Бернулли және Эйлердің туындылары жаңадан пайда болған салаға негіз
болды. Граф теориясы, сонымен бірге, төрт түсті мәселеге байланысты
қызығушылыққа себеп болды. Джероламо Кардоно өлімінен кейін жазылған
дисктерде математикалық зерттеулер туралы жазған. Бұл ойын теориясы деседе
болады. Ойын теориясына Тарталия мен Галилей қатысты. Шетелдік ойыншы
Чевалиер де Мерет пен Перре Фермат және Блейз Паскаль, онда бірнеше күрделі
комбинаторлық сұрақтар туындаған кездегі сәйкестікті ықтималдықтар теориясы
тарихына енгізді. Құмар ойындардан басқа, шифрларды жасау және оларды бұзу
үшін де криптографияда комбинаторлық әдістер қолданылды. Міне осылайша
комбинаторикалық ұғым пайда болды.
Ықтималдық
Кристиан Гюйгенс ықтималдық туралы алғашқы кітабын жариялады.Ричард
Джеффридің айтуынша, «XVII ғасырдың ортасына дейін « ықтимал » термині
мақұлданды және бұл мағынада бірден көзқарас пен іс-қимылға
қолданылды».Жәнеде, заң тұрғысынан, әсіресе, ықтимал, дәлелдемелер бар
ұсыныстарды қолдануға болады . Ықтималдық құмар ойын әсерінен туындаған.
Құмар ойын барысында ойыншыларды толғандырған сұрақтар ықтималдық
теориясын қалыптастырды.
4 слайд
ТарихКомбинаторика Комбинаторика, комбинаторикалық талдау ұғымы алғаш 1666 жылы Лейнбистің «Комбинаторлық өнерге арналған дискурстар» атты еңбегінде жарыққа шыққан. Комбинаторлық ұғымдар мен санақ нәтижелері ежелден пайда болды. Б.з.д. 6 ғасырда ежелгі үнді дәрігері Сушрута Самхита 63 түрлі дәріні 6 түрлі дәмнен жасауға болатындығын, ал бір уақытта екі рет, екеуін де бір уақытта қабылдайтынын және осылайша 26-дан 1 мүмкіндікті есептеп шығаруға шақырды. Паскаль, Ньютон, Джейкоб Бернулли және Эйлердің туындылары жаңадан пайда болған салаға негіз болды. Граф теориясы, сонымен бірге, төрт түсті мәселеге байланысты қызығушылықтың жарылысына ие болды. Джероламо Кардоно өлімінен кейін жазылған дисктерде математикалық зерттеулер туралы жазған. Бұл ойын теориясы деседе болады. Ойын теориясына Тарталия мен Галилей қатысты. Шетелдік ойыншы Чевалиер де Мерет пен Перре Фермат және Блейз Паскаль, онда бірнеше күрделі комбинаторлық сұрақтар туындаған кездегі сәйкестікті ықтималдықтар теориясы тарихына енгізді. Құмар ойындардан басқа, шифрларды жасау және оларды бұзу үшін де криптографияда комбинаторлық әдістер қолданылды. Міне осылайша комбинаторикалық ұғым пайда болды. Ықтималдық Кристиан Гюйгенс ықтималдық туралы алғашқы кітабын жариялады.Ричард Джеффридің айтуынша, « XVII ғасырдың ортасына дейін« ықтимал »термині мақұлданды және бұл мағынада бірден көзқарас пен іс- қимылға қолданылды. Алайда, заң тұрғысынан, әсіресе, ықтимал, дәлелдемелер бар ұсыныстарды қолдануға болады . Ықтималдық құмар ойын әсерінен туындаған. Құмар ойын барысында ойыншыларды толғандырған сұрақтар ықтималдық теориясын қалыптастырды. Тарих Комбинаторика Комбинаторика, комбинаторикалық талдау ұғымы алғаш 1666 жылы Лейнбистің «Комбинаторлық өнерге арналған дискурстар» атты еңбегінде жарыққа шыққан. Б.з.д. 6 ғасырда ежелгі үнді дәрігері Сушрута Самхита 63 түрлі дәріні 6 түрлі дәмнен жасауға болатындығын есептеп шығаруға шақырды. Паскаль, Ньютон, Джейкоб Бернулли және Эйлердің туындылары жаңадан пайда болған салаға негіз болды. Граф теориясы, сонымен бірге, төрт түсті мәселеге байланысты қызығушылыққа себеп болды. Джероламо Кардоно өлімінен кейін жазылған дисктерде математикалық зерттеулер туралы жазған. Бұл ойын теориясы деседе болады. Ойын теориясына Тарталия мен Галилей қатысты. Шетелдік ойыншы Чевалиер де Мерет пен Перре Фермат және Блейз Паскаль, онда бірнеше күрделі комбинаторлық сұрақтар туындаған кездегі сәйкестікті ықтималдықтар теориясы тарихына енгізді. Құмар ойындардан басқа, шифрларды жасау және оларды бұзу үшін де криптографияда комбинаторлық әдістер қолданылды. Міне осылайша комбинаторикалық ұғым пайда болды. Ықтималдық Кристиан Гюйгенс ықтималдық туралы алғашқы кітабын жариялады.Ричард Джеффридің айтуынша, «XVII ғасырдың ортасына дейін « ықтимал » термині мақұлданды және бұл мағынада бірден көзқарас пен іс-қимылға қолданылды».Жәнеде, заң тұрғысынан, әсіресе, ықтимал, дәлелдемелер бар ұсыныстарды қолдануға болады . Ықтималдық құмар ойын әсерінен туындаған. Құмар ойын барысында ойыншыларды толғандырған сұрақтар ықтималдық теориясын қалыптастырды.

#5 слайд
Комбинаторика түрлері
1.Нөмірлі комбинаторлар - комбинаторлық нысандардың санын есептеуге
арналған концентрат болып табылады.
2.Аналитикалық комбинаторлар - асимптотикалық формулаларды алуды
көздейді.
3.Экстремалды комбинаторлар - белгіленген жүйелердегі экстремалды
сұрақтарды зерттейді.
4.Ықтималды комбинаторлар - қандай да бір кездейсоқ дискретті нысан
үшін белгілі бір мүліктің ықтималдығын сипаттайды.
5.Алгебралық комбинаторлар - - дерексіз алгебра әдістерін қолданатын, әр
түрлі комбинаторлық контексттерде топтық теория мен ұсыну теориясын
қолдана алатын және керісінше, алгебрадағы мәселелерге комбинаторлық
әдістерді қолданатын математика саласы.
6.Геометриялық комбинаторлар - дөңес және дискретті геометриямен
байланысты, атап айтқанда, көпфункционалды комбинаторлар.
7.Топологиялық комбинаторика - проблемаларды және дискретті Морс
теориясын зерттеу үшін қолданылады.
8.Шексіздік комбинаторлар - Бұл жиынтық теорияның бір бөлігі,
математикалық логика саласы, бірақ теория мен экстремалды
комбинаториядан құрал және идеяларды пайдаланады.
5 слайд
Комбинаторика түрлері 1.Нөмірлі комбинаторлар - комбинаторлық нысандардың санын есептеуге арналған концентрат болып табылады. 2.Аналитикалық комбинаторлар - асимптотикалық формулаларды алуды көздейді. 3.Экстремалды комбинаторлар - белгіленген жүйелердегі экстремалды сұрақтарды зерттейді. 4.Ықтималды комбинаторлар - қандай да бір кездейсоқ дискретті нысан үшін белгілі бір мүліктің ықтималдығын сипаттайды. 5.Алгебралық комбинаторлар - - дерексіз алгебра әдістерін қолданатын, әр түрлі комбинаторлық контексттерде топтық теория мен ұсыну теориясын қолдана алатын және керісінше, алгебрадағы мәселелерге комбинаторлық әдістерді қолданатын математика саласы. 6.Геометриялық комбинаторлар - дөңес және дискретті геометриямен байланысты, атап айтқанда, көпфункционалды комбинаторлар. 7.Топологиялық комбинаторика - проблемаларды және дискретті Морс теориясын зерттеу үшін қолданылады. 8.Шексіздік комбинаторлар - Бұл жиынтық теорияның бір бөлігі, математикалық логика саласы, бірақ теория мен экстремалды комбинаториядан құрал және идеяларды пайдаланады.

#6 слайд
Комбинаториялық теориялар
1.Бөлу теориясы- алғашқы сан теориясының және
талдауының бір бөлігі, ол енді комбинаториканың
немесе тәуелсіз өрістің бөлігі болып саналады.
2.Граф теориясы - Графтар комбинаториканың негізгі
объектілері болып табылады. Құрылымдық және
алгебралық сұрақтарға жауап береді
3.Дизайн теориясы – бұл комбинаторлық
конструкцияларды зерттеу, олар белгілі бір қиылысу
қасиеттері бар ішкі жиындар жиынтығы болып табылады.
4.Тапсырыс теориясы - соңғы және шексіз де ішінара
реттелген жинақтарды зерттеу.
5.Матридо теориясы - Матроид теориясы
геометрияның бір бөлігін көрсетеді. Ол сызықтық
тәуелділік қатынасында нақты коэффициенттерге тәуелді
емес векторлық кеңістіктегі векторлардың жиынтығының
зерттейді.
6.Кодтау теориясы - қателерді түзету кодтарының ерте
комбинаторлық құрылымымен дизайн теориясының бір
бөлігі ретінде басталды.
6 слайд
Комбинаториялық теориялар 1.Бөлу теориясы- алғашқы сан теориясының және талдауының бір бөлігі, ол енді комбинаториканың немесе тәуелсіз өрістің бөлігі болып саналады. 2.Граф теориясы - Графтар комбинаториканың негізгі объектілері болып табылады. Құрылымдық және алгебралық сұрақтарға жауап береді 3.Дизайн теориясы – бұл комбинаторлық конструкцияларды зерттеу, олар белгілі бір қиылысу қасиеттері бар ішкі жиындар жиынтығы болып табылады. 4.Тапсырыс теориясы - соңғы және шексіз де ішінара реттелген жинақтарды зерттеу. 5.Матридо теориясы - Матроид теориясы геометрияның бір бөлігін көрсетеді. Ол сызықтық тәуелділік қатынасында нақты коэффициенттерге тәуелді емес векторлық кеңістіктегі векторлардың жиынтығының зерттейді. 6.Кодтау теориясы - қателерді түзету кодтарының ерте комбинаторлық құрылымымен дизайн теориясының бір бөлігі ретінде басталды.
#7 слайд
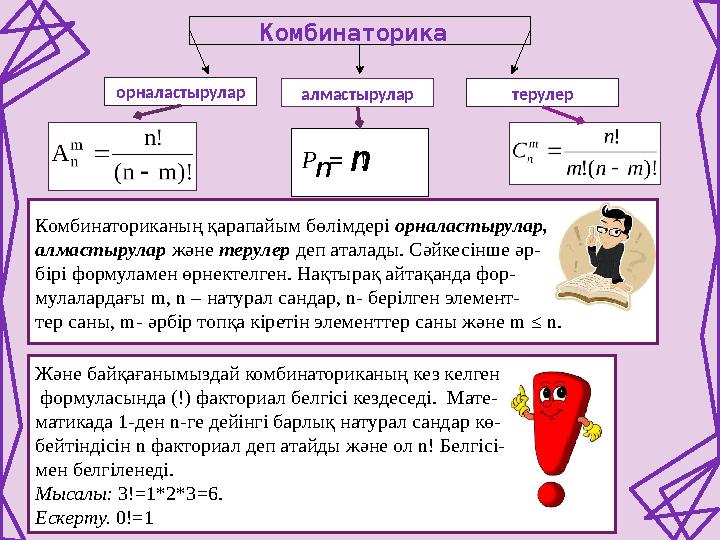
Комбинаторика
орналастырулар
алмастырулар терулер
n n
Комбинаториканың қарапайым бөлімдері орналастырулар,
алмастырулар және терулер деп аталады. Сәйкесінше әр-
бірі формуламен өрнектелген. Нақтырақ айтақанда фор-
мулалардағы m, n – натурал сандар, n- берілген элемент-
тер саны, m - әрбір топқа кіретін элементтер саны және m ≤ n .
Және байқағанымыздай комбинаториканың кез келген
формуласында (!) факториал белгісі кездеседі. Мате-
матикада 1-ден n- ге дейінгі барлық натурал сандар кө-
бейтіндісін n факториал деп атайды және ол n ! Белгісі-
мен белгіленеді.
Мысалы: 3!=1*2*3 = 6.
Ескерту. 0! = 1
7 слайд
Комбинаторика орналастырулар алмастырулар терулер n n Комбинаториканың қарапайым бөлімдері орналастырулар, алмастырулар және терулер деп аталады. Сәйкесінше әр- бірі формуламен өрнектелген. Нақтырақ айтақанда фор- мулалардағы m, n – натурал сандар, n- берілген элемент- тер саны, m - әрбір топқа кіретін элементтер саны және m ≤ n . Және байқағанымыздай комбинаториканың кез келген формуласында (!) факториал белгісі кездеседі. Мате- матикада 1-ден n- ге дейінгі барлық натурал сандар кө- бейтіндісін n факториал деп атайды және ол n ! Белгісі- мен белгіленеді. Мысалы: 3!=1*2*3 = 6. Ескерту. 0! = 1

#8 слайд
1-мысал. Сыныптағы 20
оқушыны екі-екіден
орналастырудың неше тәсілі бар?
Шешуі: Орналастырулар
формуласымен қарастырсақ
n= 20, m= 2 380 20 * 19
18 * 17 * ... * 4 * 3 * 2 * 1
20 * 19 * 18 * .... * 4 * 3 * 2 * 1
! 18
! 20
)! 2 20(
! 20 2
20
А
Жауабы: 380 тәсілі бар.
8 слайд
1-мысал. Сыныптағы 20 оқушыны екі-екіден орналастырудың неше тәсілі бар? Шешуі: Орналастырулар формуласымен қарастырсақ n= 20, m= 2 380 20 * 19 18 * 17 * ... * 4 * 3 * 2 * 1 20 * 19 * 18 * .... * 4 * 3 * 2 * 1 ! 18 ! 20 )! 2 20( ! 20 2 20 А Жауабы: 380 тәсілі бар.
#9 слайд
15
2
30
2 * 1
6 * 5
4 * 3 * 2 * 1 * 2 * 1
6 * 5 * 4 * 3 * 2 * 1
! 4! 2
! 6
)! 2 6(! 2
! 6 2
6
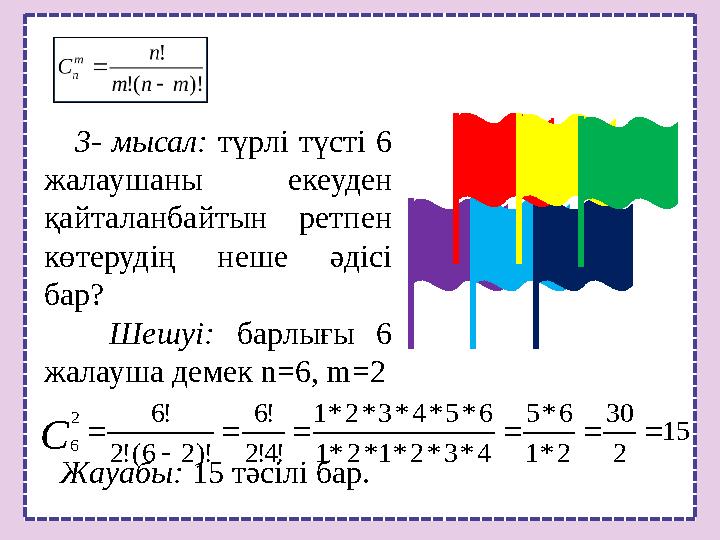
С 3- мысал: түрлі түсті 6
жалаушаны екеуден
қайталанбайтын ретпен
көтерудің неше әдісі
бар?
Шешуі: барлығы 6
жалауша демек n=6, m=2
Жауабы: 15 тәсілі бар.
9 слайд
15 2 30 2 * 1 6 * 5 4 * 3 * 2 * 1 * 2 * 1 6 * 5 * 4 * 3 * 2 * 1 ! 4! 2 ! 6 )! 2 6(! 2 ! 6 2 6 С 3- мысал: түрлі түсті 6 жалаушаны екеуден қайталанбайтын ретпен көтерудің неше әдісі бар? Шешуі: барлығы 6 жалауша демек n=6, m=2 Жауабы: 15 тәсілі бар.

#10 слайд
2–мысал: Қызыл, көк және жасыл үш үстелді
қайталанбайтын неше ретпен орналастырсақ
болады?
Шешуі: Алмастырулар формуласы арқыл
есептейміз. 3 үстел болғандықтан n=3
26 3 * 2 * 1 ! 3
3
P
Жауабы: 6 ретпен орналастыруға болады
10 слайд
2–мысал: Қызыл, көк және жасыл үш үстелді қайталанбайтын неше ретпен орналастырсақ болады? Шешуі: Алмастырулар формуласы арқыл есептейміз. 3 үстел болғандықтан n=3 26 3 * 2 * 1 ! 3 3 P Жауабы: 6 ретпен орналастыруға болады

#11 слайд
Көбейту Қосу
Z жиынының элементтерінің
әрқайсысына K элементтерін
сәйкестендіруге болады.2*3 =6 Z жиынынан немесе K жиынынан 1
элементт і таңдаудың неше тәсілі бар?
2 +3=5Комбинаторикада екі негізгі
амалдар көбейту және қосу.
Мысалы: 2 жейде мен 3 галстук
берілсін. Осы галстуктармен
жейделерді қайталамай киюге
болады. Алдымен бірінші
жейдемен 3 галстук 3 күн бойы.
Келесі жейдеменде солай. Яғни
3*2=6.
Жиындармен қарастырсақ:
Z=( ақ, қызыл ) Z=2
K=( сары, көк, ала ) K=3
11 слайд
Көбейту Қосу Z жиынының элементтерінің әрқайсысына K элементтерін сәйкестендіруге болады.2*3 =6 Z жиынынан немесе K жиынынан 1 элементт і таңдаудың неше тәсілі бар? 2 +3=5Комбинаторикада екі негізгі амалдар көбейту және қосу. Мысалы: 2 жейде мен 3 галстук берілсін. Осы галстуктармен жейделерді қайталамай киюге болады. Алдымен бірінші жейдемен 3 галстук 3 күн бойы. Келесі жейдеменде солай. Яғни 3*2=6. Жиындармен қарастырсақ: Z=( ақ, қызыл ) Z=2 K=( сары, көк, ала ) K=3

#12 слайд
Ықтималдық
Ықтималдық тарихта құмар ойынның даму кезеңінде пайда
болғандығы туралы айтылғын. Ал құмар ойында әрбір жағдай
кездейсоқ болады. Оны нақты ешбірі нақтылай алмайды. Ал
ықтималдылық қаншалықты мүмкін екендігін көрсетеді.
Форумуладағы m, n – натурал сандар, n- барлық жағдай саны,
m - керекті жағдай саны және m ≤ n .
12 слайд
Ықтималдық Ықтималдық тарихта құмар ойынның даму кезеңінде пайда болғандығы туралы айтылғын. Ал құмар ойында әрбір жағдай кездейсоқ болады. Оны нақты ешбірі нақтылай алмайды. Ал ықтималдылық қаншалықты мүмкін екендігін көрсетеді. Форумуладағы m, n – натурал сандар, n- барлық жағдай саны, m - керекті жағдай саны және m ≤ n .

#13 слайд
Есеп: Үстел үстіндегі 3 ойын сүйегін тастағанда
тақ сандардың түсу ықтималдығы қанша?
Шешуі: Әрбір ойын сүйегінде 6 беткейі бар.
Оның 3-еуі тақ болса барлық жағдайлар саны
6*3 = 18 , ал керекті жағдайлар саны 3*3 = 9, m=9;
n=18 ,5. 0
18
9
Р
Жауабы: 0.5 ықтималдығы
13 слайд
Есеп: Үстел үстіндегі 3 ойын сүйегін тастағанда тақ сандардың түсу ықтималдығы қанша? Шешуі: Әрбір ойын сүйегінде 6 беткейі бар. Оның 3-еуі тақ болса барлық жағдайлар саны 6*3 = 18 , ал керекті жағдайлар саны 3*3 = 9, m=9; n=18 ,5. 0 18 9 Р Жауабы: 0.5 ықтималдығы

#14 слайд
Түйін!
Қандай жағдай болмасын әркез математика
адам өміріне қажет. Ал математика
бөлімдерінің ішінде комбинаторика мен
ықтималдық аса қажет. Математиканы жақсы
білсек қандай жұмыс болмасын нақты және
дұрыс бастап одан әрмен қарай дамыта
аламыз. Сондықтан әрбір сәт ізденісте болған
жөн!
14 слайд
Түйін! Қандай жағдай болмасын әркез математика адам өміріне қажет. Ал математика бөлімдерінің ішінде комбинаторика мен ықтималдық аса қажет. Математиканы жақсы білсек қандай жұмыс болмасын нақты және дұрыс бастап одан әрмен қарай дамыта аламыз. Сондықтан әрбір сәт ізденісте болған жөн!

#15 слайд
15 слайд

шағым қалдыра аласыз
















