Комбинаторика. Ньютон биномы.

1 слайд
Карыбаева Сауле Шешкеновна –Шығыс Қазақстан облысы, Үржар ауданы, Қарақол орта мектеп-бақшасының математика пәні мұғалімі

1 слайд

2 слайд
Комбинаторикаға кіріспе.   Берілген жиындағы элементтерден қандай да бір шартқа бағынатын әртүрлі қанша комбинация құрастыруға болады деген сұрақты қарастыратын математика саласын комбинаторика деп атайды. Комбинаторика ұғымы XVI - ғасырда пайда болған. Комбинаториканың дамуы Я.Бернулли, Лейбниц, Эйлер есімдерімен тығыз байланысты. Соңғы жылдары комбинаторика жедел даму үстінде. Комбинаторикалық әдістер транспорттық есептер шешуде, кестелер, өндірістік жоспарлар құрастыруда және өнімді өткізу мәселесінде қолданылады. Комбинаторика автоматтар теориясында, экономикалық есептерде, биология және генетикада қолданылады. Математиканың бұл бағытына ең алғаш ат беріп, өзінің 1666 жылғы «Об искусстве комбинаторики» еңбегінде «комбинаторный» терминін ең алғаш қолданған, неміс тіл танушысы, философ және математигі Готфрид Вильгельм Лейбниц (1646–1716).

2 слайд

3 слайд
Комбинаторика – ақырлы жиындарды құрастыру әдістерін зерттейді. Комбинаторика екі түрлі есептерді зерттейді: таңдау есептерін және орналастыру есептерін. Таңдау есептерінде берілген жиыннан элементтерді таңдап алудың ережелері анықталады. Орналастыру есептерінде берілген элементтерден жаңа жиындар құралады. Комбинаторикалық конфигурациялардың негізгі түрлеріне мыналар жатады:  алмастырулар  терулер  орналастырулар

3 слайд

4 слайд
  ! ! m n п А т п  Қайталанбайтын орналастыру Анықтама: берілген n элементтен бір бірінен құрамы немесе орналасу ретімен өзгеше болатын m элементтер таңдамасын n элементтен алынған m элементті қайталанбайтын орналастыру деп атайды. 1-мысал. 1, 2, 3, 4, 5 цифрлар арқылы цифрлары қайталанбайтын қанша а) екі таңбалы, үш таңбалы, төрт таңбалы, бес таңбалы сандар құрастыруға болады? Шешуі:

4 слайд

5 слайд
m m n n A Қайталанбалы орналастырулар. Анықтама. Егер бір таңдамада бір элемент 2, 3, …n рет қайталанса, онда оны п элементтен m элементті қайталанатын орналастырулар деп атайды. 1-мысал: 1, 2, 3, 4, 5 цифрлар арқылы цифрлары қайталанатын неше екі таңбалы, үш таңбалы, төрт таңбалы, бес таңбалы сандар құрастыруға болады. Шешуі:

5 слайд

6 слайд
Қайталанбайтын алмастырулар . Анықтама . Егер қайталанбайтын орналастыру формуласында m= n болса , онда - қайталанбайтын алмастыру деп аталады . 1-мысал. а) 2, 3, 4 цифрлары арқылы қанша үш таңбалы сан жазуға болады. б) 2, 3, 4, 7 цифрлары арқылы қанша төрт таңбалы сан жазуға болады. Санды жазғанда цифрлар қайталанбайды. Шешуі: Р п = n !

6 слайд

7 слайд
Қайталанатын алмастырулар. P = n! n !n !…n ! 1 12 2k k n ;n ;…;n

7 слайд

8 слайд
Қайталанатын алмастырулар. 1-мысал. а) Т, Ә , У , Л , І , К ; б) С , А, Х , А, Р , А . әріптерінен қанша сөз (мағынасыз) құрастыруға болады. Шешуі: а) мұнда әріптер әр түрлі болғандықтан Р 6 =6! Сонымен Т, Ә , У , Л , І , К әріптерінен Р 6 = 6! = 720 әр түрлі сөз құрастыруға болады. б) Мұнда қайталанбайтын алмастыруды қолдануға болмайды, себебі

8 слайд

9 слайд

9 слайд

10 слайд
Қайталанбайтын терулер C = n! m!(n-m)!n m

10 слайд

11 слайд
1-мысал . А, В, С, D төрт элементтен 2 элементті қайталанбайтын орналастырулар және терулер санын табу керек. Шешуі . Орналастыру формуласы бойынша n=4, m=2 болғанда Ал n = 4, m=2 болғанда, терудің саны : АВ АС АD ВС ВD СD мұнда элементтердің орналасу реті маңызды емес.

11 слайд

12 слайд
Теру санын есептеу қасиеттері

12 слайд

13 слайд
Қайталанатын теру

13 слайд

14 слайд
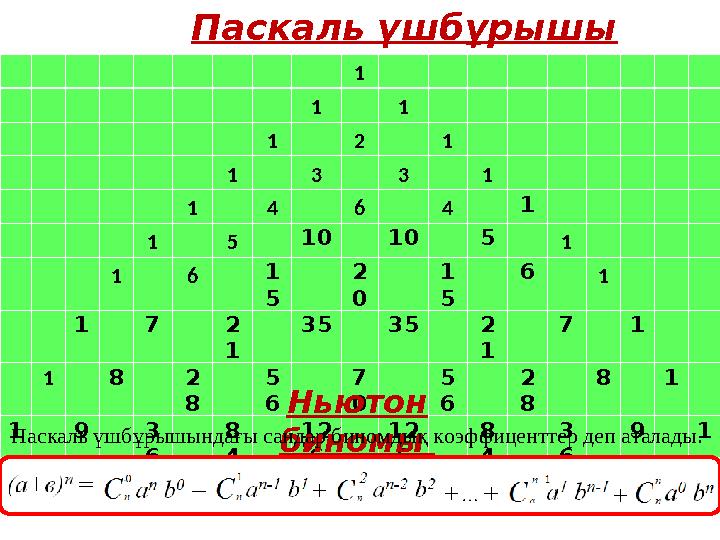
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 1 5 2 0 1 5 6 1 1 7 2 1 35 35 2 1 7 1 1 8 2 8 5 6 7 0 5 6 2 8 8 1 1 9 3 6 8 4 12 6 12 6 8 4 3 6 9 1Паскаль үшбұрышы Ньютон биномы Паскаль үшбұрышындағы сандар биномдық коэффиценттер деп аталады.

14 слайд

15 слайд
n ;n ;…;n Р п = n !  ! ! m n п А т п   m m n n A  P = n! n !n !…n ! 1 12 2k k

15 слайд