Материалдар / Квадрат теңдеу түріне келтірілетін жоғары дәрежелі теңдеулер

Квадрат теңдеу түріне келтірілетін жоғары дәрежелі теңдеулер

Материал туралы қысқаша түсінік

Нурмуханбетова Дария Уахитовна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

04 Қараша 2024

0 рет жүктелген

Алгебра Презентация 10 сынып

450 ₸

Бүгін алсаңыз
+23 бонус беріледі
Бұл не?

Бүгін алсаңыз +23 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 17

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Сабақ тақырыбы

1 слайд

Сабақ тақырыбы

2 слайд
Oқу мақсаты: 10.2.3.9 тригонометриялық теңдеулерді көбейткіштерге жіктеу арқылы шешу;

2 слайд

Oқу мақсаты: 10.2.3.9 тригонометриялық теңдеулерді көбейткіштерге жіктеу арқылы шешу;

3 слайд
Сабақ мақсаттары: - қарапайым тригонометриялық теңдеулерді шешу үшін қажетті тригонометриялық формулаларды білу және қорыту; - қарапайым тригонометриялық теңдеулерді көбейткіштерге жіктеу тәсілі арқылы шешуді үйрену.

3 слайд

Сабақ мақсаттары: - қарапайым тригонометриялық теңдеулерді шешу үшін қажетті тригонометриялық формулаларды білу және қорыту; - қарапайым тригонометриялық теңдеулерді көбейткіштерге жіктеу тәсілі арқылы шешуді үйрену.

4 слайд
БАҒАЛАУ КРИТЕРИЙІ: - қарапайым тригонометриялық теңдеулерді шешу үшін қажетті тригонометриялық формулаларды біледі; - қарапайым тригонометриялық теңдеулерді көбейткіштерге жіктеу тәсілі арқылы шешуді үйренеді.

4 слайд

БАҒАЛАУ КРИТЕРИЙІ: - қарапайым тригонометриялық теңдеулерді шешу үшін қажетті тригонометриялық формулаларды біледі; - қарапайым тригонометриялық теңдеулерді көбейткіштерге жіктеу тәсілі арқылы шешуді үйренеді.

5 слайд
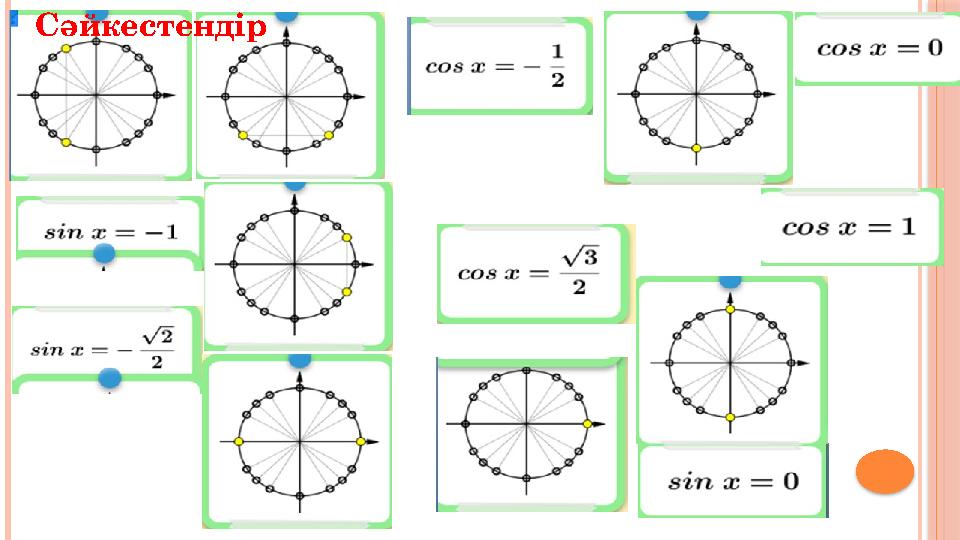
Сәйкестендір

5 слайд

Сәйкестендір

6 слайд
КӨБЕЙТКІШТЕРГЕ ЖІКТЕУ ӘДІСІ Тригонометриялық теңдеулерді ұсынылатын әдіспен шешу кезінде, алгебралық өрнектерді көбейткіштерге жіктеудің барлық әдісін, яғни ортақ көбейткішті жақша сыртына шығару, топтау, қысқаша көбейту формулаларын қолдануға болады. Көбейткіштерге жіктеген кезде, тригонометриялық теңдеудің оң жағы нөлге тең болуы керек. Осылайша, күрделі тригонометриялық теңдеу бірнеше қарапайым теңдеулерге жіктеледі. Мына формулаларды білген дұрыс: тригонометриялық функциялардың қосындысын көбейткішке жіктеу; тригонометриялық функциялардың көбейтіндісін қосылғыштарға жіктеу.

6 слайд

КӨБЕЙТКІШТЕРГЕ ЖІКТЕУ ӘДІСІ Тригонометриялық теңдеулерді ұсынылатын әдіспен шешу кезінде, алгебралық өрнектерді көбейткіштерге жіктеудің барлық әдісін, яғни ортақ көбейткішті жақша сыртына шығару, топтау, қысқаша көбейту формулаларын қолдануға болады. Көбейткіштерге жіктеген кезде, тригонометриялық теңдеудің оң жағы нөлге тең болуы керек. Осылайша, күрделі тригонометриялық теңдеу бірнеше қарапайым теңдеулерге жіктеледі. Мына формулаларды білген дұрыс: тригонометриялық функциялардың қосындысын көбейткішке жіктеу; тригонометриялық функциялардың көбейтіндісін қосылғыштарға жіктеу.

7 слайд
Теңдеуді шеш: Косинустардың айырмасын формула бойынша көбейткіштерге жіктейміз: Алынған екі шешімді бір шешімге біріктіреміз: Тригонометриялық функциялардың көбейтіндісін қосылғыштарға жіктеу формуласын қолданамыз:

7 слайд

Теңдеуді шеш: Косинустардың айырмасын формула бойынша көбейткіштерге жіктейміз: Алынған екі шешімді бір шешімге біріктіреміз: Тригонометриялық функциялардың көбейтіндісін қосылғыштарға жіктеу формуласын қолданамыз:

8 слайд
Мысал-1. cos 2x – cos 8x + cos 6x = 1. cos 2x + cos 6x = 1 + cos 8x , 2 cos 4x cos 2x = 2 cos ² 4x , cos 4x · ( cos 2x – cos 4x ) = 0 , cos 4x · 2 sin 3x · sin x = 0 , 1) cos 4x = 0 , 2) sin 3x = 0 , 3) sin x = 0 ,    2 4x , nx3 , mx 48  x , 3 n x  . Жауабы: 48  x , 3 n x  , mx. №1 мысал

8 слайд

Мысал-1. cos 2x – cos 8x + cos 6x = 1. cos 2x + cos 6x = 1 + cos 8x , 2 cos 4x cos 2x = 2 cos ² 4x , cos 4x · ( cos 2x – cos 4x ) = 0 , cos 4x · 2 sin 3x · sin x = 0 , 1) cos 4x = 0 , 2) sin 3x = 0 , 3) sin x = 0 ,    2 4x , nx3 , mx 48  x , 3 n x  . Жауабы: 48  x , 3 n x  , mx. №1 мысал

9 слайд
Көбейткіштерді жеке-жеке нөлге теңдеп аламыз. , №2 мысал

9 слайд

Көбейткіштерді жеке-жеке нөлге теңдеп аламыз. , №2 мысал

10 слайд
Көбейткіштерге жіктеу тәсілі Дескрипторлар теңдеудің сол жағын көбейткіштерге жіктейді тригонометрия формулаларын қолданады қарапайым тригонометриялық теңдеулердің шешімдерінің жалпы формулаларын қолданады жауабын жазады

10 слайд

Көбейткіштерге жіктеу тәсілі Дескрипторлар теңдеудің сол жағын көбейткіштерге жіктейді тригонометрия формулаларын қолданады қарапайым тригонометриялық теңдеулердің шешімдерінің жалпы формулаларын қолданады жауабын жазады

11 слайд
Көбейткіштерге жіктеу тәсілі

11 слайд

Көбейткіштерге жіктеу тәсілі

12 слайд
Мысал – 3. 1 – cosx = tgx – sinx; Мысал – 4. 1 + sinx = ctgx + cosx. Дескриптор: •түрлендіру формулаларын біледі; •көбейткіштерге жіктейді; •әр көбейткіш үшін х – ті табады. •жауабын дұрыс жазады.

12 слайд

Мысал – 3. 1 – cosx = tgx – sinx; Мысал – 4. 1 + sinx = ctgx + cosx. Дескриптор: •түрлендіру формулаларын біледі; •көбейткіштерге жіктейді; •әр көбейткіш үшін х – ті табады. •жауабын дұрыс жазады.

13 слайд
Тест тапсырмасы 1 2 3 4

13 слайд

Тест тапсырмасы 1 2 3 4

14 слайд

15 слайд
Жұптық жұмыс тапсырмалары: №1. cos2x = sinx – cosx Жауабы: .2 2 ;2; 4 mn      №2. sin 2 3x + sin 2 4x = sin 2 5x + sin 2 6x. Жауабы: . 2 ; 9    n №3. 1+sinx = ctgx + cosx. Жауабы: .2 2 ; 4     n Өз бетімен орындауға арналған тапсырмалар Дескриптор: •түрлендіру формулаларын біледі; •көбейткіштерге жіктейді; •әр көбейткіш үшін х – ті табады. •жауабын дұрыс жазады.

15 слайд

Жұптық жұмыс тапсырмалары: №1. cos2x = sinx – cosx Жауабы: .2 2 ;2; 4 mn      №2. sin 2 3x + sin 2 4x = sin 2 5x + sin 2 6x. Жауабы: . 2 ; 9    n №3. 1+sinx = ctgx + cosx. Жауабы: .2 2 ; 4     n Өз бетімен орындауға арналған тапсырмалар Дескриптор: •түрлендіру формулаларын біледі; •көбейткіштерге жіктейді; •әр көбейткіш үшін х – ті табады. •жауабын дұрыс жазады.

16 слайд
Рефлексия

16 слайд

Рефлексия