Квадрат теңсіздік
Материал туралы қысқаша түсінік
Материал жас мамандарға және математика мұғалімдеріне. Ашық есік күнінде өткізуге болатын сабақ
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 6
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
Тақырыбы: Квадрат
теңсіздік.Квадрат теңсіздікті квадрат
функцияның графигі арқылы шешу
Сабақтың міндеттері:
•
Квадрат функцияның қасиеттерін қайталау.
•
Кавдрат теңсіздікті графиктік тәсілмен
шешу дағдысын үйрену.
1 слайд
Тақырыбы: Квадрат теңсіздік.Квадрат теңсіздікті квадрат функцияның графигі арқылы шешу Сабақтың міндеттері: • Квадрат функцияның қасиеттерін қайталау. • Кавдрат теңсіздікті графиктік тәсілмен шешу дағдысын үйрену.
2 слайд
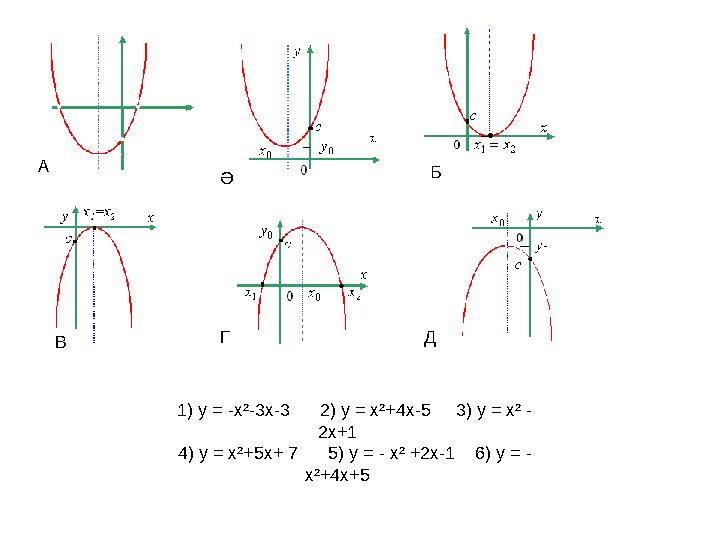
1) у = -х²-3х-3 2) у = х²+4х-5 3) у = х² -
2х+1
4) у = х²+5х+ 7 5) у = - х² +2х-1 6) у = -
х²+4х+5А
В Ә Б
Г Д
2 слайд
1) у = -х²-3х-3 2) у = х²+4х-5 3) у = х² - 2х+1 4) у = х²+5х+ 7 5) у = - х² +2х-1 6) у = - х²+4х+5А В Ә Б Г Д
3 слайд
Бір айнымалысы бар екінші
дәрежелі теңсіздікті шешу
алгоритмі
1.5х 2
+9х-2 <0
2 .y= 5х 2
+9х-2 функциясын
қарастырамыз
3 . Тармағы жоғары бағытталған
парабола.
4. 5х 2
+9х-2= 0
х
1 =-2; х
2 =
5.5
1
X
Y
-2
5
1 01. Теңсіздікті a x 2
+ b x+ c >0
( a x 2
+ b x+ c < 0) түріне келтіру
2. y= a x 2
+ b x+ c функциясын
қарастырамыз
3 . Парабола тармақтарының
бағытын анықтау
4. Параболаның ох осін қиятын
нүктелерін анықтау ( a x 2
+ b x+ c =0
теңдеуін шешіп ; х
1 және х
2
табамыз
5. y= a x 2
+ b x+ c схемалық графигін
саламыз
6. y >0 (y<0) болатындай
параболаның бөлігін көрсетеміз Теңсіздікті шешу мысалы
3 слайд
Бір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі 1.5х 2 +9х-2 <0 2 .y= 5х 2 +9х-2 функциясын қарастырамыз 3 . Тармағы жоғары бағытталған парабола. 4. 5х 2 +9х-2= 0 х 1 =-2; х 2 = 5.5 1 X Y -2 5 1 01. Теңсіздікті a x 2 + b x+ c >0 ( a x 2 + b x+ c < 0) түріне келтіру 2. y= a x 2 + b x+ c функциясын қарастырамыз 3 . Парабола тармақтарының бағытын анықтау 4. Параболаның ох осін қиятын нүктелерін анықтау ( a x 2 + b x+ c =0 теңдеуін шешіп ; х 1 және х 2 табамыз 5. y= a x 2 + b x+ c схемалық графигін саламыз 6. y >0 (y<0) болатындай параболаның бөлігін көрсетеміз Теңсіздікті шешу мысалы
4 слайд
5
1
X
Y-2
5
1 01 Теңсіздікті a x 2
+ b x+ c >0
( a x 2
+ b x+ c < 0) түріне келтіру
2. y= a x 2
+ b x+ c функциясын
қарастырамыз
3 . Парабола тармақтарының
бағытын анықтау
4. Параболаның ох осін қиятын
нүктелерін анықтау
( a x 2
+ b x+ c =0 теңдеуін шешіп ; х
1
және х
2 табамыз
5. y= a x 2
+ b x+ c схемалық
графигін саламыз
6. y >0 (y<0) болатындай
параболаның бөлігін
көрсетеміз
7. Абсцисса осінен y>0 (y<0)
болатындай х-тің мәнін
көрсетеміз Теңсіздікті шешу мысалыБір айнымалысы бар екінші
дәрежелі теңсіздікті шешу
алгоритмі
1.5х 2
+9х-2 <0
2 .y= 5х 2
+9х-2 функциясын
қарастырамыз
3 . Тармағы жоғары бағытталған
парабола.
4. 5х 2
+9х-2= 0
х
1 =-2; х
2 =
5.
4 слайд
5 1 X Y-2 5 1 01 Теңсіздікті a x 2 + b x+ c >0 ( a x 2 + b x+ c < 0) түріне келтіру 2. y= a x 2 + b x+ c функциясын қарастырамыз 3 . Парабола тармақтарының бағытын анықтау 4. Параболаның ох осін қиятын нүктелерін анықтау ( a x 2 + b x+ c =0 теңдеуін шешіп ; х 1 және х 2 табамыз 5. y= a x 2 + b x+ c схемалық графигін саламыз 6. y >0 (y<0) болатындай параболаның бөлігін көрсетеміз 7. Абсцисса осінен y>0 (y<0) болатындай х-тің мәнін көрсетеміз Теңсіздікті шешу мысалыБір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі 1.5х 2 +9х-2 <0 2 .y= 5х 2 +9х-2 функциясын қарастырамыз 3 . Тармағы жоғары бағытталған парабола. 4. 5х 2 +9х-2= 0 х 1 =-2; х 2 = 5.
5 слайд
ір айнымалысы бар екінші
дәрежелі теңсіздікті шешу
алгоритмі
1.5х 2
+9х-2 <0
2 .y= 5х 2
+9х-2 функциясын
қарастырамыз
3 . Тармағы жоғары бағытталған
парабола.
4. 5х 2
+9х-2= 0
х
1 =-2; х
2 =
5.
8 . х Є(-2; )5
1
X
Y-2
5
1 0
5
11. Теңсіздікті a x 2
+ b x+ c >0
( a x 2
+ b x+ c < 0) түріне келтіру
2. y= a x 2
+ b x+ c функциясын
қарастырамыз
3 . Парабола тармақтарының
бағытын анықтау
4. Параболаның ох осін қиятын
нүктелерін анықтау ( a x 2
+ b x+ c =0
теңдеуін шешіп ; х
1 және х
2
табамыз
5. y= a x 2
+ b x+ c схемалық графигін
саламыз
6. y >0 (y<0) болатындай
параболаның бөлігін көрсетеміз
7. Абсцисса осінен y>0 (y<0)
болатындай х-тің мәнін
көрсетеміз
8. Аралықпен жауабын жазу Теңсіздікті шешу мысалы
5 слайд
ір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі 1.5х 2 +9х-2 <0 2 .y= 5х 2 +9х-2 функциясын қарастырамыз 3 . Тармағы жоғары бағытталған парабола. 4. 5х 2 +9х-2= 0 х 1 =-2; х 2 = 5. 8 . х Є(-2; )5 1 X Y-2 5 1 0 5 11. Теңсіздікті a x 2 + b x+ c >0 ( a x 2 + b x+ c < 0) түріне келтіру 2. y= a x 2 + b x+ c функциясын қарастырамыз 3 . Парабола тармақтарының бағытын анықтау 4. Параболаның ох осін қиятын нүктелерін анықтау ( a x 2 + b x+ c =0 теңдеуін шешіп ; х 1 және х 2 табамыз 5. y= a x 2 + b x+ c схемалық графигін саламыз 6. y >0 (y<0) болатындай параболаның бөлігін көрсетеміз 7. Абсцисса осінен y>0 (y<0) болатындай х-тің мәнін көрсетеміз 8. Аралықпен жауабын жазу Теңсіздікті шешу мысалы
