Квадрат үшмүше

#1 слайд
Квадрат үшмүше. Квадрат үшмүшені көбейткіштерге жіктеу. Алгебра 8 сынып

1 слайд

#2 слайд
1. Квадрат үшмүшені көбейткіштерге жіктеу тәсілдерін білу және есеп шығаруда тиімді қолдану; 2. Жеке, жұппен, топпен ынтымақтастықта жұмыс жасай білуге дағдыландыру,өзін – өзі және топты бағалай білуге үйрету; 3. Өз ойын еркін жеткізуге, ой пікірімен бөлісе білуге, шығармашылыққа ұмтылдыру.

2 слайд

#3 слайд
Психологиялық дайындық: Көңіл күйлеріңіз қалай ? Күшті Жақсы Орташа

3 слайд

#4 слайд
1.Қандай теңдеу квадрат теңдеу деп аталады? 2.Егер теңдеуіндегі в немесе с нөлге тең болса, онда ол теңдеулер қандай теңдеулер болады? 3.Квадрат теңдеуді шешудің қандай әдістерін білесіңдер?

4 слайд

#5 слайд
Квадрат теңдеулерге келтірілетін есептерді шешу ежелгі вавилондықтарда кездеседі. Олардың біздің заманымызға дейінгі 2000 жылдары толымсыз квадрат теңдеулерді шеше білгендіктерін айрықтайтын қол жазбалар сақталған. Ежелгі грек математиктері кейбір квадрат теңдеулерді геометриялық салу есептеріне келтіріп шеше білген. Мәселен, александриялық Диофант (ІІІ ғ.) aх=b және түріндегі теңдеулерді шешу тәсілдерін көрсете білген. VІІ ғасырда үнді ғалымы Брахматгупта түріндегі теңдеулерді шешу ережелерін көрсеткен,ал орта азиялық ғұлама ғалым әл – Хорезми (ХІІғ.) өзінің атақты “Китаб әл – джебр валь – мукабала” деген еңбегінде түріндегі теңдеулерді шешу формуласының сөйлемдік тұжырымдамасын келтірген. Квадрат теңдеуді шешудің жалпы түрі мен оның түбірлерінің теңдеудің коэффиценттеріне тәуелділігін өрнектейтін формулаларды Ф. Виет 1591 жылы ұсынған. Бірақ Ф. Виет теңдеулердің тек оң түбірлерін қарастырған. Квадрат теңдеулердің теріс түбірлерін ескеруді алғашқылар қатарында болып Италия ғалымдары Н. Тарталья , Кардано, Бомбелли ұсынған.

5 слайд

#6 слайд
Берілген жауаптарды қолданып, сөйлемді аяқтаЖауаптары 1. теңдеу квадрат теңдеу деп аталады, егер ... 2. Теңдеу келтірілген квадрат теңдеу деп аталады, егер... 3. Теңдеу толымсыз квадрат теңдеу деп аталады, егер... 4. теңдеуінің екі түбірі болады,егер... 5. теңдеудің бір түбірі болады,егер... 6. теңдеуінің түбірі болмайды, егер... b=0 c=0 a=0 b≠0 a≠0 D=0 D<0 D>0

6 слайд

#7 слайд
• Егер квадрат үшмүшенің түбірлері бар болса, онда теңдігі орындалады; • Егер квадрат үшмүшенің бір түбірі бар болса, онда квадрат үшмүшені түрінде жіктеуге болады; • Егер квадрат үшмүшенің түбірлері табылмаса, онда квадрат үшмүше көбейткіштерге жіктеуге болмайды.

7 слайд

#8 слайд

8 слайд

#9 слайд

9 слайд

#10 слайд

10 слайд

#11 слайд

11 слайд

#12 слайд

12 слайд

#13 слайд

13 слайд

#14 слайд

14 слайд

#15 слайд

15 слайд

#16 слайд

16 слайд

#17 слайд

17 слайд

#18 слайд

18 слайд

#19 слайд

19 слайд

#20 слайд
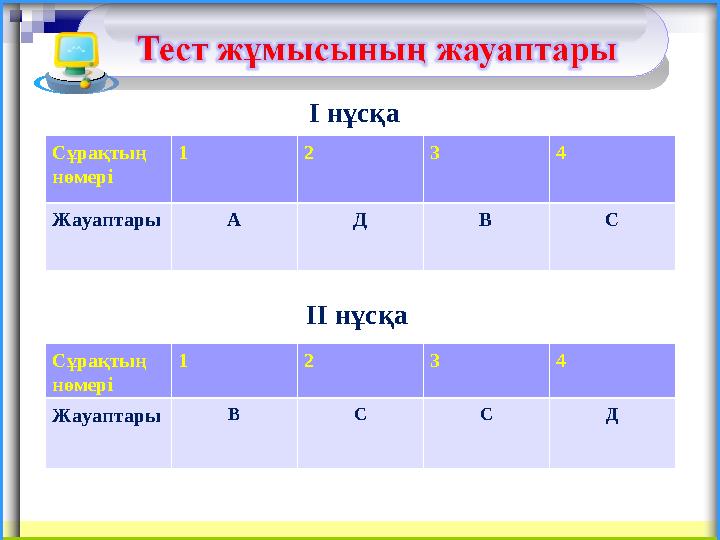
Сұрақтың нөмері 1 2 3 4 Жауаптары А Д В С Сұрақтың нөмері 1 2 3 4 Жауаптары В С С Д І нұсқа ІІ нұсқа

20 слайд

#21 слайд

21 слайд

#22 слайд
№233 §4

22 слайд