Maple -жүйесі

1 слайд
Ғылыми жоба авторы: Нарымбетов Дархан

1 слайд

2 слайд
Жоспар.   Кіріспе Maple жүйесі дегеніміз қандай программа? Бұл жүйені кейбір математика сабақтарында қолданудың маңыздылығы қандай? II. Негізгі бөлім 1 . Марle жүйесінде кейбір арнайы функцияларды енгізу және жүйеге бұйрық беру 2. Марle жүйесінде ‘‘solve’’ бұйрығын қолданып элементар математика есептерін шығару 3. Марle жүйесінде ‘‘plot ’’ бұйрығын қолданып функцияның графигін салу III. Қорытынды бөлім Болашақта барлық ғылым салалары компьютерлік бағдарламалармен тығыз байланыста болады IV. Əдебиеттер

2 слайд

3 слайд
Maple ж үйесінде кейбір арнайы функцияларды енгізу cosx cos( x ) tg x tan( x ) ctg x cot( x ) arcsinx arcsin(x) arccosx arccos(x) arc tg x arc tan( x) arc ctgx arccot ( x) n x ^ x n q p x ^ ( / ) x p q x ( ) sqrt x sin x   sin x

3 слайд

4 слайд
x e exp( ) x x a ^ ( ) a x log a x log[ ]( ) a x x x  ^ ( ) x   shx sinh(x) chx cosh(x) thx tanh(x) cthx coth(x) lnx ln(x) lgx abs(x) і I l g[10]( )o x

4 слайд

5 слайд
[ > - бұйрықты енгізу облысы. [ - берілген есептің мәтінін енгізу облысы. ( Т - пернесін басу арқылы шығарылады ). Enter – ді басқан соң көк түсті өрнекпен шығатын аймақ мәтін шешімі болып саналады. Кез-кеген бұйрық restart – сөзімен басталады және ( ;) немесе ( :) белгісімен аяқталады.( ;) - белгісі нәтижені экранға шығарады, ал (:) - белгісі нәтижені экранға шығармайды.

5 слайд

6 слайд
:= p   a 5 12 7Maple жүйесінде функцияны меншіктеу үшін латын әріптері қолданылады . Функцияның атын енгізген соң ( :)- белгісін және (=)- белгісін қойып , функцияның мәнін енгіземіз. p:=(a+5=12); 1- мысал . a+5=12 теңдеуді шешіңіз: [ > restart; [ > p:=(a+5=12); [ > solve(p,a); Жауабы: 7 .

6 слайд

7 слайд
2 2 7 7 x   := h   2 x 2 7 7 , 7  7 7 72-мысал. [ > restart; [ > h:=sqrt(2*x^2-7)=sqrt(7); [ > solve(h,x); Жауабы: ; - .теңдеуді шешіңіз:

7 слайд

8 слайд
Maple – жүйесінде теңдеуді , теңсіздікті , теңдеулер жүйесін және теңсіздіктер жүйесін шешуде solve – бұйрығы қолданылады. Теңдеудің түбірін табу үшін келесі амалды орындаймыз. [ > solve(f(x),x); немесе функцияны меншіктеп g:=f(x) алып [ > solve(g,x); есептеуге болады.

8 слайд

9 слайд
2 15 16 0 x x    , 16 -1 := k    x 2 15 x 16 0 , 16 -1 1 16 x  2 1 x 1- мысал . [ > restart; [ > solve(x^2-15*x-16=0,x); немесе берілген теңдеуді меншіктеп алып төмендегідей үлгіде есептеуге болады. [ > restart; [ > k:=x^2-15*x-16=0; [ > solve(k,x); Жауабы: теңдеудің түбірлері , тең . теңдеуді шешіңіз:

9 слайд

10 слайд
2 2 2 ( 6 ) 5( 6 ) 24 x x x x     := d    ( )  x 2 6 x 2 5 x 2 30 x 24 , , ,   3 6   3 6   3 17   3 17 5 3 0 x x   := d   x 5 x 3 0 , , , , 0 0 0 1 -12-мысал. [ > restart; [ > d:=(x^2+6*x)^2-5*(x^2+6*x)=24; [ > solve(d,x); 3-мысал. [ > restart; [ > d:=x^5-x^3=0; [ > solve(d,x); теңдеуді шешіңіз: теңдеуді шешіңіз:

10 слайд

11 слайд
 Maple – жүйесінде теңсіздікті шешуде solve – бұйрығы қолданылады. Maple – жүйесінде теңсіздік белгілерін келесі түрде енгіземіз. < < > > >= <= ( 8)( 5) 0 x x    := h  0 ( )  x 8 ( )  x 5 , ( ) RealRange ,   ( ) Open -8 ( ) RealRange , ( ) Open 5  ( ; 8) (5; ).    1 -мысал. [ > restart; [ > h:=(x+8)*(x-5)>0; [ > solve(h,x); Жауабы: теңсіздікті шешіңізТеңсіздіктің шешіміндегі Open- сөзімен көрсетілген мәндер (аралықтар) теңсіздік шешіміне кірмейді.

11 слайд

12 слайд
Maple – да теңдеулер жүйесін шешуде solve – бұйрығы қолданылады. Теңдеулер жүйесін шешу үшін жүйенің берілген әрбір функциясын меншіктеп f:=f(x) , g:=g(x) [ > solve({f,g},{x,y}); амалын орындаймыз. Немесе [> h:={f(x),g(x)}; [> solve(h,{x,y}); амалын орындаймыз. Немесе [> solve({f(x),g(x)},{x,y}); амалын орындау арқылы шығаруға болады.

12 слайд

13 слайд
2 1, 3; y x x y        , { } ,  y -1  x 2 { } ,  x 5  y 2 := f   y 2 x -1 := g  x  y 3 , { } ,  y -1  x 2 { } ,  x 5  y 21- мысал . [> restart; [> solve({y^2-x=-1,x=y+3}, {x,y}); Немесе әрбір функцияны меншіктеп алып [> restart; [> f:=y^2-x=-1; [> g:=x=y+3; [> solve({f,g},{x,y}); Есептеуге болады. Жауабы: (2 ; - 1 ) , (5; 2).теңдеулер жүйесін шешіңіз:

13 слайд

14 слайд
5, 1, 2, 0, 4. x y z u y z u v z u v x u v x y v x y z                             := f     x y z u 5 := g     y z u v 1 := k     z u v x 2 := p     u v x y 0 := h     v x y z 4 { } , , , ,  u -1 y 1 z 3 x 2 v -22- мысал . [> restart; [> f:=x+y+z+u=5; [> g:=y+z+u+v=1; [> k:=z+u+v+x=2; [> p:=u+v+x+y=0; [> h:=v+x+y+z=4; [> solve({f,g,k,p,h}, {x,y,z,u,v}); теңдеулер жүйесін шешіңіз: Жауабы: u=-1, y=1 , z=3 , x=2 , v=-2 .

14 слайд

15 слайд
Maple – да теңсіздіктер жүйесін шешуде solve – бұйрығы қолданылады.  Maple – жүйесінде теңсіздік белгілерін келесі түрде енгіземіз. < < > > <= >= Теңсіздіктер жүйесін шешу үшін жүйенің берілген әрбір функциясын меншіктеп f:=f(x) ,g:=g(x) [ > solve({f,g},{x}); амалын орындаймыз. Немесе [> h:={f(x),g(x)}; [> solve(h,{x}); амалын орындаймыз. Немесе [> solve({f(x),g(x)},{x}); амалын орындау арқылы шығаруға болады. Maple – жүйесінде

15 слайд

16 слайд
2 1 0, 2 18 0; x x        := f  x -1 := g  0  2 x 2 18 { }  x -3 ( ; 3).   1- мысал . [> restart; [> f:=x+1<0; [> g:=2*x^2-18>0; [> solve({f,g},{x}); Жауабы: теңсіздіктер жүйесін шешіңіз:

16 слайд

17 слайд
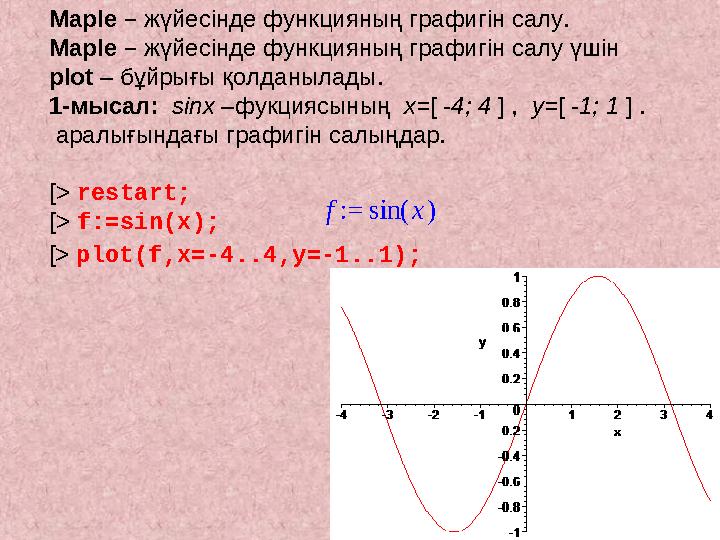
:= f ( ) sin xMaple – жүйесінде функцияның графигін салу. Maple – жүйесінде функцияның графигін салу үшін plot – бұйрығы қолданылады. 1-мысал: sinx – фукциясының x= [ - 4 ; 4 ] , y= [ - 1 ; 1 ] . аралығындағы графигін салыңдар. [> restart; [> f:=sin(x); [> plot(f,x=-4..4,y=-1..1);

17 слайд

18 слайд
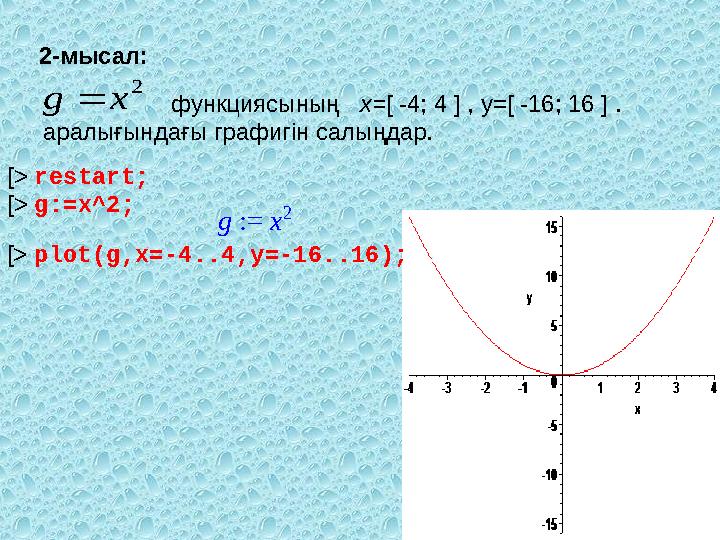
2 g x  := g x 22-мысал: [ > restart; [> g:=x^2; [> plot(g,x=-4..4,y=-16..16); функциясының x= [ -4; 4 ] , y=[ -16; 16 ] . аралығындағы графигін салыңдар.

18 слайд