#1 слайд
«Тригонометрия» сөзі алғаш рет 1505 жылы неміс теологы және математигі Питискус еңбегінде кездеседі. Бұл сөз грек тілінен алынған және «үшбұрышты өлшеу туралы ғылым» деп аударылады.

1 слайд

#2 слайд
Синус ұғымының ұзақ тарихы бар. Үшбұрыштың кесінділерінің және шеңбердің әр түрлі қатыстары (тригонометриялық функциялар) туралы мәлімет б.э.д. III ғасырлардағы Ежелгі Грецияның ұлы математиктері - Евклид, Архимед, Апполоний Пергский еңбектерінде кездесті.

2 слайд

#3 слайд
IV-V ғасырларда-ақ ұлы үнді ғалымы Ариабхаттың (476 – 550 шамас.) астрономия бойынша еңбектерінде арнайы термин пайда болды. CB кесіндісін ол ардхаджива (ардха – жарты, джива – адырна, ол хорданы еске салады) деп атады. Артынан анағұрлым қысқаша джива деп аталды. Араб математиктері IX ғасырда бұл сөзді арабша джайб (дөңестік) деген сөзбен алмастырды. Арабша математикалық мәтіндерді аударуда XII ғасырда ол латынша синус (sinus –қатпар, қисықтық) деген сөзбен алмастырылды.

3 слайд

#4 слайд

4 слайд

#5 слайд
Тангенстер көлеңкенің ұзындығын анықтау туралы есепті шешумен байланысты пайда болды. Тангенсті, сонымен бірге котангенсті XI ғасырда Араб математигі Абу-л-Вафа енгізді,ол сонымен бірге тангенстер мен котангенстерді табуға арналған алғаш кестелерді құрастырған болатын. Дей тұрғанмен, бұл ашылулар ұзақ уақыт бойы еуропа ғалымдарына беймәлім болды, сондықтан тангенстерді XIV ғасырда әуелі ағылшын ғалымы Т.Брадвердин, соңынан неміс математигі Региомонтан(1467г.) қайта ашқан. «Тангенс» деген аталуы латынның «tanger» (жанасу) деген сөзінен шыққан және тек 1583 жылы ғана пайда болды.

5 слайд

#6 слайд

6 слайд

#7 слайд
Тригонометриялық функцияларды анықтаудың бірнеше тәсілдері бар. Оларды екі топқа бөлуге болады: аналитикалық және геометриялық. 1.Аналитикалық тәсілдерге у = sin х функциясынf (х)=-c*f(х) дифференциалдық теңдеуінің шешімі ретінде анықтау немесе sin х = х - х3 /3!+ х5 /5! - … дәрежелік қатарының қосындысы ретінде анықтау жатады 2. Геометриялық тәсілдерге тригонометриялық функцияларды радиус- вектордың координаталары мен проекциялары негізінде анықтау, тік бұрышты үшбұрыштың қабырғаларының қатыстары арқылы анықтау және сандық шеңбер көмегімен анықтауды жатқызады. Мектеп курсында қарапайымдылығы мен көрнекілігіне қарай геометриялық тәсілдер арқылы анықтауға жүгінеді.

7 слайд

#8 слайд
БҰРЫШТЫҢ СИНУСЫ, КОСИНУСЫ ЖӘНЕ ТАНГЕНСІН АНЫҚТАУ Бірлік шеңбердің бастапқы нүктесінен х бұрышына бұрғаннан алынған А нүктесінің ординатасы х санының синусы, А нүктесінің абсциссасы х санының косинусы деп аталады. Х санының синусының оның косинусына қатынасы х санының тангенсі деп, ал х санының косинусының оның синусына қатынасы х санының котангенсі деп аталады. у=sin x, у=cosx, у=tgx и у= ctg x функциялары Тригонометриялық функциялар деп аталады.

8 слайд

#9 слайд
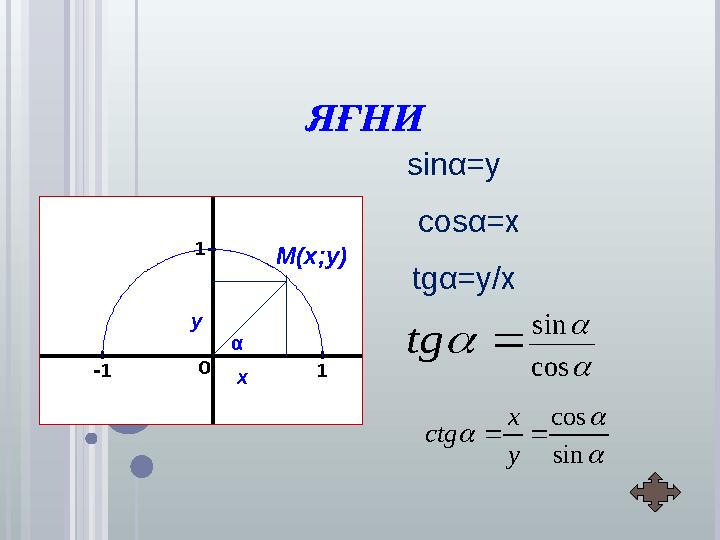
ЯҒНИ X Y -2 -1 1 2 -2 -1 1 2 0 х у sinα=y cosα=x tgα=у/х М(х;у)    sin cos  y x ctg   cos sin tgα

9 слайд

#10 слайд
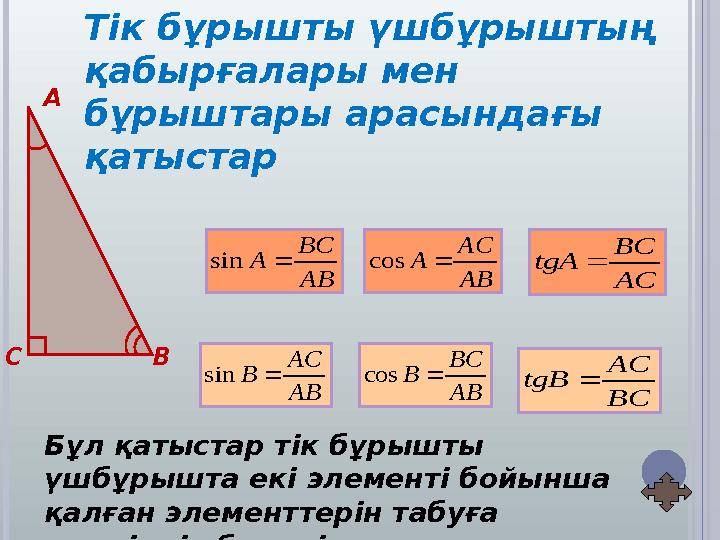
А С В AB AC Acos AC BC tgA AB BC Bcos BC AC tgB AB BC Asin AB AC Bsin Тік бұрышты үшбұрыштың қабырғалары мен бұрыштары арасындағы қатыстар Бұл қатыстар тік бұрышты үшбұрышта екі элементі бойынша қалған элементтерін табуға мүмкіндік береді.

10 слайд

#11 слайд
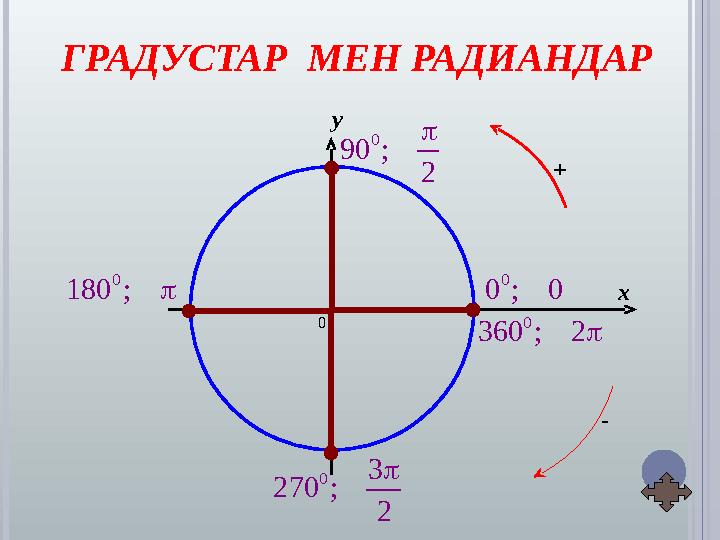
0 x y + 0 0; 0 0 90; 2  0 180; 03 270; 2  0 360; 2 ГРАДУСТАР МЕН РАДИАНДАР -

11 слайд

#12 слайд
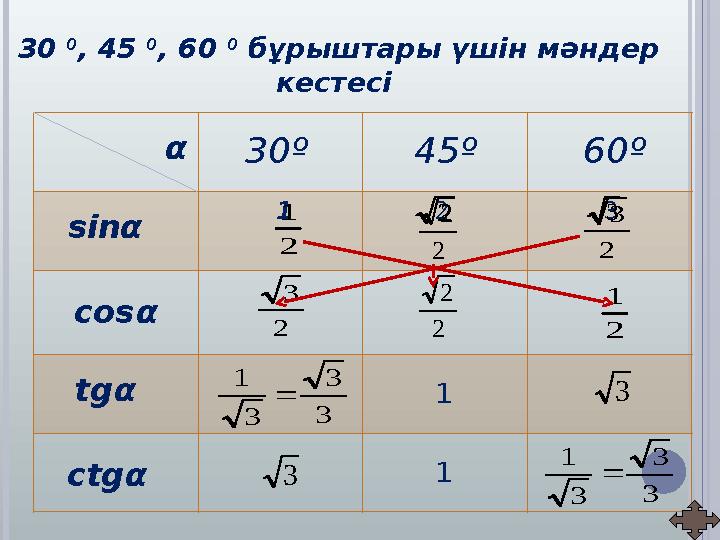
30º 60º45º αsin α α α α cos tg ctg 1 2 32 3 2 1 2 2 2 3 2 1 2 2 2 3 3 3 3 1  1 3 3 3 1 1 3 3 30 0 , 45 0 , 60 0 бұрыштары үшін мәндер кестесі

12 слайд

#13 слайд
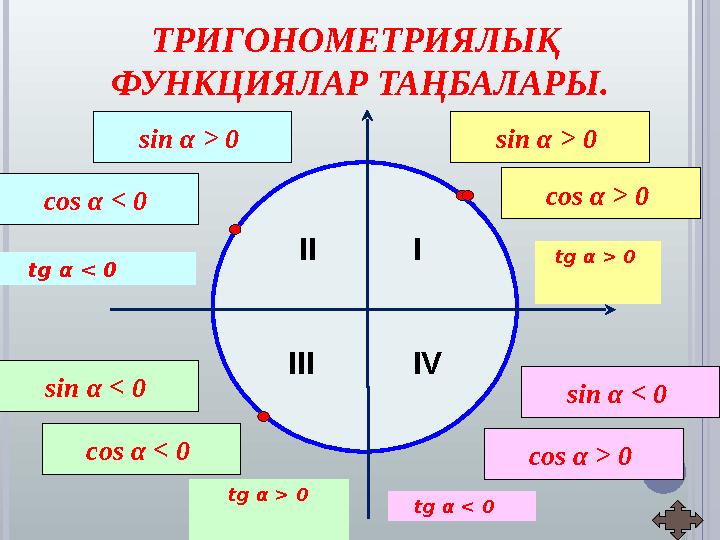
ТРИГОНОМЕТРИЯЛЫҚ ФУНКЦИЯЛАР ТАҢБАЛАРЫ. III III IV sin α > 0 cos α > 0 sin α > 0 cos α < 0 sin α < 0 cos α < 0 sin α < 0 cos α > 0 tg α < 0 tg α > 0 tg α > 0 tg α < 0

13 слайд

#14 слайд
ТРИГОНОМЕТРИЯЛЫҚ ТЕҢБЕ-ТЕҢДІКТЕР   2 2 sin 1 1ctg    sin cos ctg1ctgtg    cos sin tg 1 2 tg  2 cos 1 1sincos 22 

14 слайд