2024-2025 оқу жылына арналған
қысқа мерзімді сабақ жоспарларын
Жүктеп алғыңыз келеді ме?
ҚР Білім және Ғылым министірлігінің стандартымен жасалған
Модулі бар квадрат теңдеулерді шешу
Материал туралы қысқаша түсінік
Тест жауабымен+ көп есептер+ жеке топтық жұптық
Авторы:
24 Қараша 2024
147
0 рет жүктелген
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 24
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
Сабақтың тақырыбы:
Модулі бар квадрат теңдеулерді
шешу
1 слайд
Сабақтың тақырыбы: Модулі бар квадрат теңдеулерді шешу
2 слайд
Оқу мақсаты:
8.2.2.5 |ax
2
+bx|+c=0; ax
2
+b|x|+c=0
түріндегі теңдеулерді шешу
2 слайд
Оқу мақсаты: 8.2.2.5 |ax 2 +bx|+c=0; ax 2 +b|x|+c=0 түріндегі теңдеулерді шешу
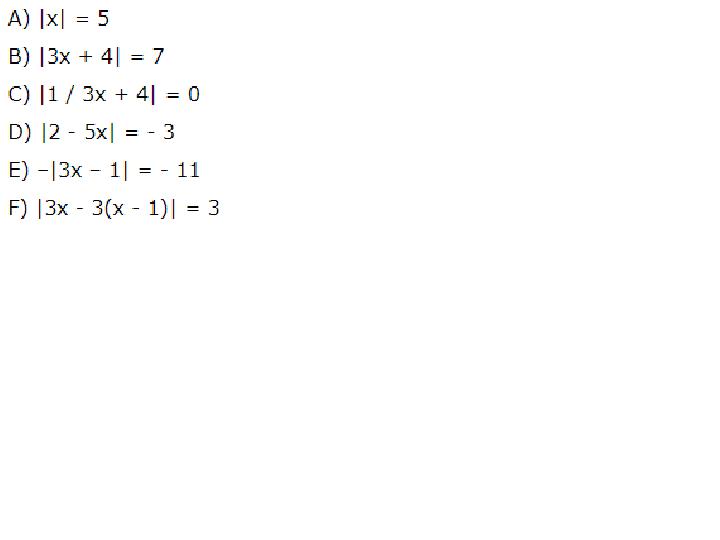
3 слайд
3 слайд
4 слайд
1. Теңдеуді шешіңіз
A.
B.
C.
D.
02,1
2
xx
6
5
;0
5
6
;0
6
5
;1
2;
5
6
4 слайд
1. Теңдеуді шешіңіз A. B. C. D. 02,1 2 xx 6 5 ;0 5 6 ;0 6 5 ;1 2; 5 6
5 слайд
2. Теңдеуді шешіңіз =4,2
A. -0,7
B. 0,7
C. -0,7; 0,7;
D. -1 ; 1
E. Ø
х6
7
3
7
3
5 слайд
2. Теңдеуді шешіңіз =4,2 A. -0,7 B. 0,7 C. -0,7; 0,7; D. -1 ; 1 E. Ø х6 7 3 7 3
6 слайд
4. Теңдеуді шешіңіз:
A. 3
B. -3
C.
D.
E. Түбірі жоқ
)52(25 xx
3
5
5
3
6 слайд
4. Теңдеуді шешіңіз: A. 3 B. -3 C. D. E. Түбірі жоқ )52(25 xx 3 5 5 3
7 слайд
1. Егер квадрат теңдеудің екі түбірі де
нөлге тең болса, онда оның түрі
төмендегідей болады:
A.
B.
C.
D.
E.
0
2
cbxax
0
2
bxax
0
2
ax
0
2
cax
0
2
cbxax
7 слайд
1. Егер квадрат теңдеудің екі түбірі де нөлге тең болса, онда оның түрі төмендегідей болады: A. B. C. D. E. 0 2 cbxax 0 2 bxax 0 2 ax 0 2 cax 0 2 cbxax
8 слайд
2. Квадрат теңдеудің түбірлері
қарама-қарсы сандар болса, оның
түрі төмендегідей болады:
A.
B.
C.
D. , мұндағы а және с –
бірдей таңбалы сандар
E. , мұндағы а және с –
таңбалары әртүрлі сандар
0
2
cbxax
0
2
bxax
0
2
ax
0
2
cax
0
2
cax
8 слайд
2. Квадрат теңдеудің түбірлері қарама-қарсы сандар болса, оның түрі төмендегідей болады: A. B. C. D. , мұндағы а және с – бірдей таңбалы сандар E. , мұндағы а және с – таңбалары әртүрлі сандар 0 2 cbxax 0 2 bxax 0 2 ax 0 2 cax 0 2 cax
9 слайд
3. Квадрат теңдеудің бір түбірі 0-ге
тең болса, оның түрі төмендегідей
болады:
A.
B.
C.
D. , мұндағы а және с –
бірдей таңбалы сандар
E. , мұндағы а және с –
таңбалары әртүрлі сандар
0
2
cbxax
0
2
bxax
0
2
ax
0
2
cax
0
2
cax
9 слайд
3. Квадрат теңдеудің бір түбірі 0-ге тең болса, оның түрі төмендегідей болады: A. B. C. D. , мұндағы а және с – бірдей таңбалы сандар E. , мұндағы а және с – таңбалары әртүрлі сандар 0 2 cbxax 0 2 bxax 0 2 ax 0 2 cax 0 2 cax
10 слайд
4. теңдеуінің
түбірлерінің қосындысы:
A. 7
B. -7
C. -3,5
D. 3,5
E. 3
10 слайд
4. теңдеуінің түбірлерінің қосындысы: A. 7 B. -7 C. -3,5 D. 3,5 E. 3
11 слайд
5. теңдеуі берілген.
Төмендегі тұжырымдардың қайсысы жалған?
A. Егер a + b + c = 0, онда теңдеудің бір түбірі 1-
ге тең.
B. Егер a – b + c = 0, онда теңдеудің бір түбірі -1-
ге тең.
C. Түбірлердің көбейтіндісі –с/а-ға тең.
D. Егер дискриминат 0-ге тең болса, онда
теңдеудің екі түбірі тең.
0
2
cbxax
11 слайд
5. теңдеуі берілген. Төмендегі тұжырымдардың қайсысы жалған? A. Егер a + b + c = 0, онда теңдеудің бір түбірі 1- ге тең. B. Егер a – b + c = 0, онда теңдеудің бір түбірі -1- ге тең. C. Түбірлердің көбейтіндісі –с/а-ға тең. D. Егер дискриминат 0-ге тең болса, онда теңдеудің екі түбірі тең. 0 2 cbxax
12 слайд
Тұжырымдардың қайсысы
ақиқат?
A. | -1,25 | = 1,25
B. | -14/2 | = - 7
C. | x | = x
D. | -5 | + | 3 | = | -5 + 3 |
E. | a + b| = | a | + | b |
12 слайд
Тұжырымдардың қайсысы ақиқат? A. | -1,25 | = 1,25 B. | -14/2 | = - 7 C. | x | = x D. | -5 | + | 3 | = | -5 + 3 | E. | a + b| = | a | + | b |
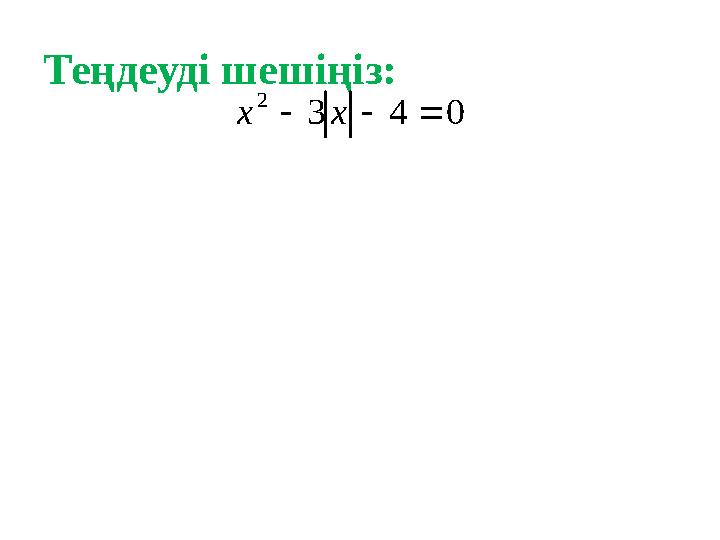
13 слайд
Теңдеуді шешіңіз:
043
2
xx
13 слайд
Теңдеуді шешіңіз: 043 2 xx
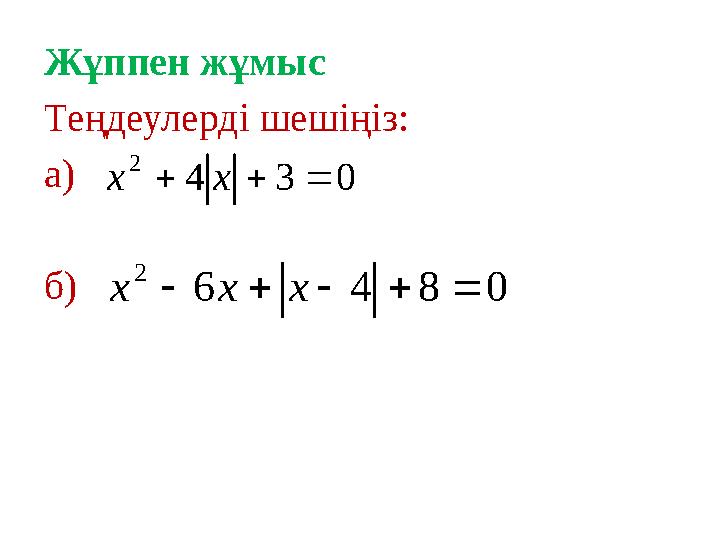
14 слайд
Жұппен жұмыс
Теңдеулерді шешіңіз:
а)
б)
034
2
xx
0846
2
xxx
14 слайд
Жұппен жұмыс Теңдеулерді шешіңіз: а) б) 034 2 xx 0846 2 xxx
15 слайд
Өзіндік жұмыс
Теңдеулерді шешіңіз:
а) ;
б) ;
в) ;
г) .
15 слайд
Өзіндік жұмыс Теңдеулерді шешіңіз: а) ; б) ; в) ; г) .
16 слайд
№1. Модульдің анықтамасын пайдаланып, теңдеуді шешіңіз:
16 слайд
№1. Модульдің анықтамасын пайдаланып, теңдеуді шешіңіз:
17 слайд
№2. Модульдің анықтамасын пайдаланып, теңдеуді шешіңіз:
17 слайд
№2. Модульдің анықтамасын пайдаланып, теңдеуді шешіңіз:
18 слайд
18 слайд
19 слайд
19 слайд
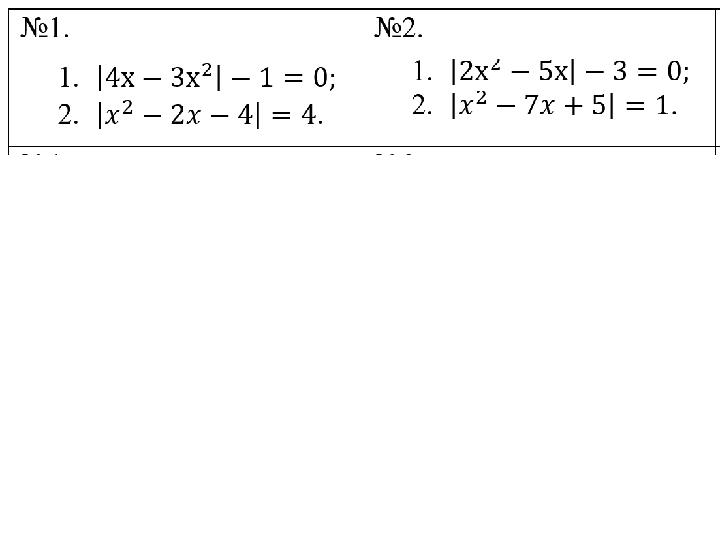
20 слайд
20 слайд
21 слайд
21 слайд
22 слайд
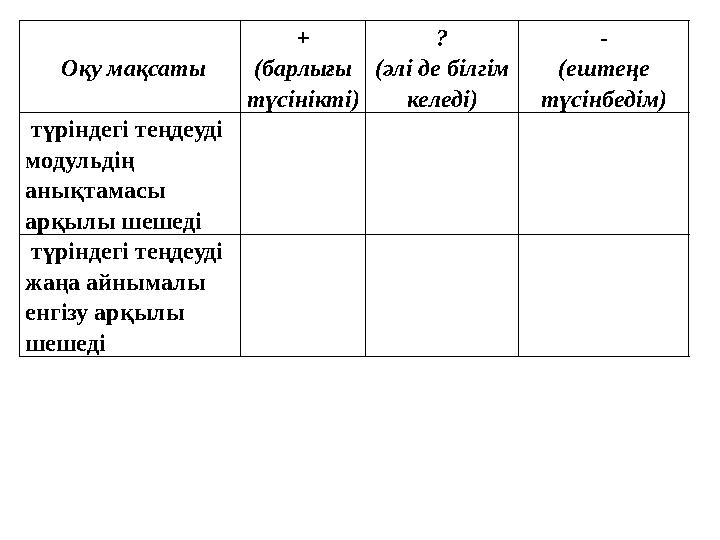
Оқу мақсаты
+
(барлығы
түсінікті)
?
(әлі де білгім
келеді)
-
(ештеңе
түсінбедім)
түріндегі теңдеуді
модульдің
анықтамасы
арқылы шешеді
түріндегі теңдеуді
жаңа айнымалы
енгізу арқылы
шешеді
22 слайд
Оқу мақсаты + (барлығы түсінікті) ? (әлі де білгім келеді) - (ештеңе түсінбедім) түріндегі теңдеуді модульдің анықтамасы арқылы шешеді түріндегі теңдеуді жаңа айнымалы енгізу арқылы шешеді
23 слайд
Үй тапсырмасы
1. Теңдеулерді шешіңіз:
а)
б)
2. Өрнекті ықшамдаңыз:
034
2
xx
0334
2
xxx
23 слайд
Үй тапсырмасы 1. Теңдеулерді шешіңіз: а) б) 2. Өрнекті ықшамдаңыз: 034 2 xx 0334 2 xxx
