Материалдар / Негізгі тригонометриялық тепе - теңдіктер

Негізгі тригонометриялық тепе - теңдіктер

Материал туралы қысқаша түсінік

Дайын презентация: анықтама + формула + есептер

Умарбеков Абдуллах Даниярович

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

24 Қараша 2024

0 рет жүктелген

Алгебра Барлық материалдар 9 сынып

250 ₸

Бүгін алсаңыз
+13 бонус беріледі
Бұл не?

Бүгін алсаңыз +13 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 10

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

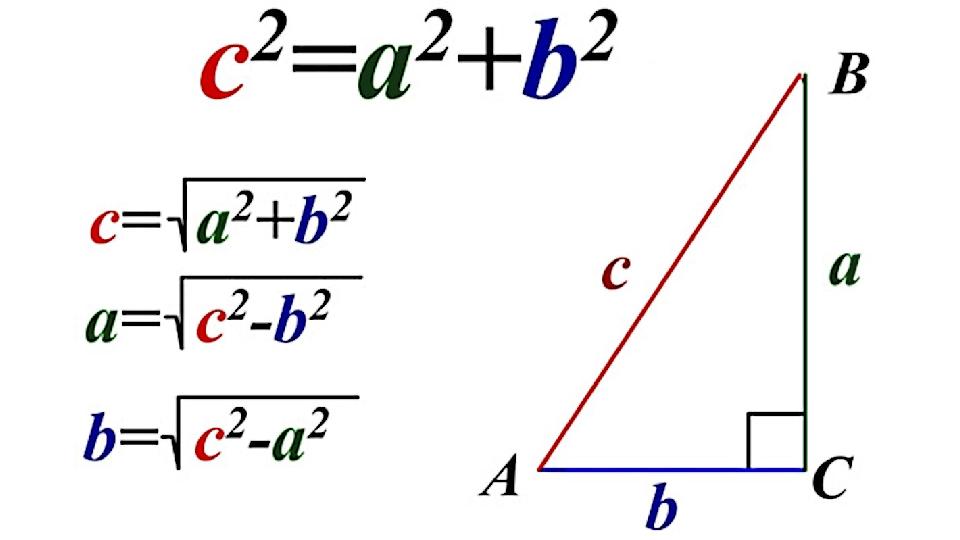
2 слайд

3 слайд
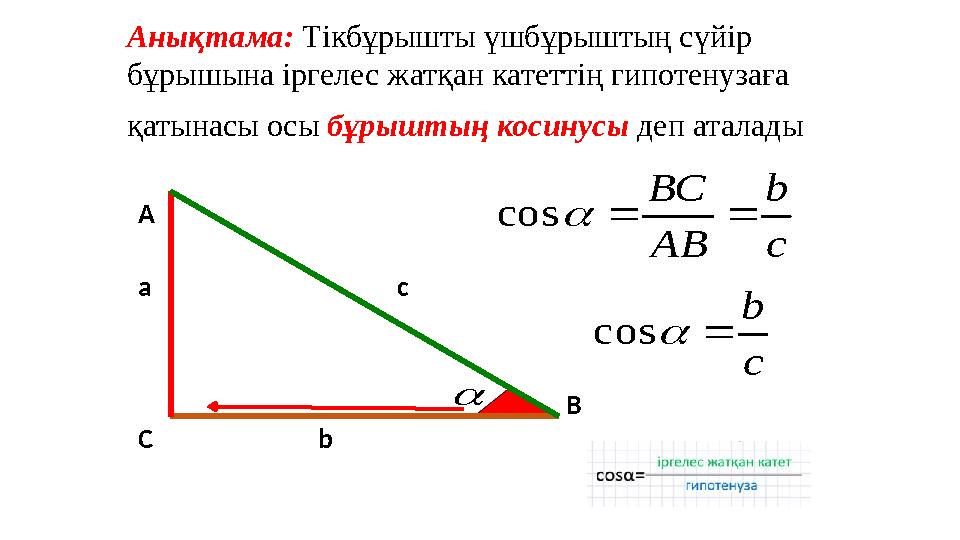
А С В b ca c b АВ ВС cos Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің гипотенузаға қатынасы осы бұрыштың косинусы деп аталады c b cos 

3 слайд

А С В b ca c b АВ ВС cos Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің гипотенузаға қатынасы осы бұрыштың косинусы деп аталады c b cos 

4 слайд
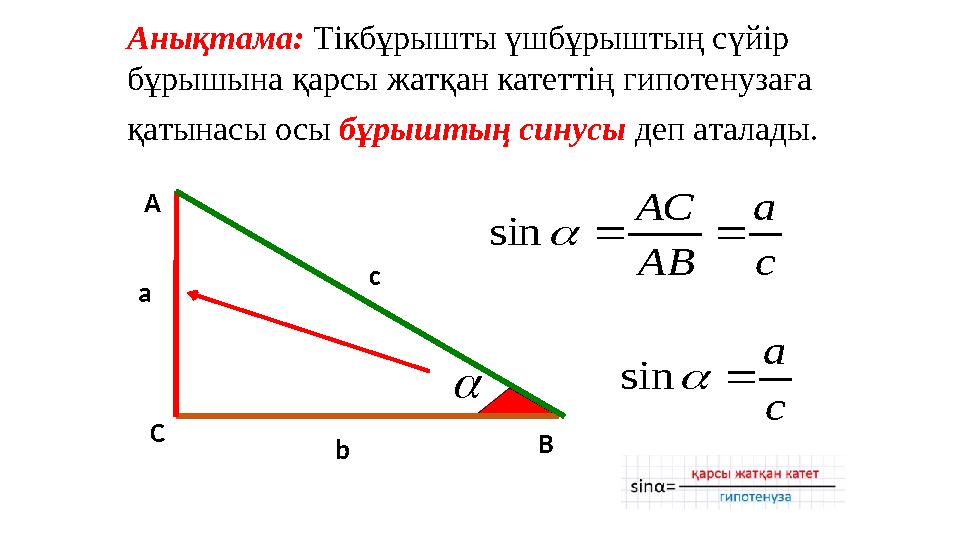
А С Вb c a c a АВ АС sin Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің гипотенузаға қатынасы осы бұрыштың синусы деп аталады.  c a sin

4 слайд

А С Вb c a c a АВ АС sin Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің гипотенузаға қатынасы осы бұрыштың синусы деп аталады.  c a sin

5 слайд
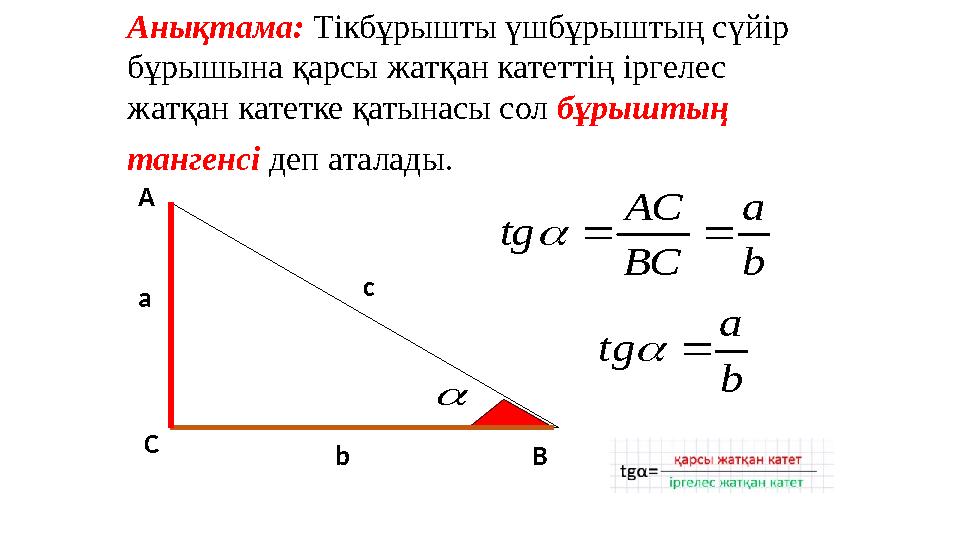
А С Вb c a b a ВС АС tg  Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің іргелес жатқан катетке қатынасы сол бұрыштың тангенсі деп аталады. b a tg 

5 слайд

А С Вb c a b a ВС АС tg  Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына қарсы жатқан катеттің іргелес жатқан катетке қатынасы сол бұрыштың тангенсі деп аталады. b a tg 

6 слайд
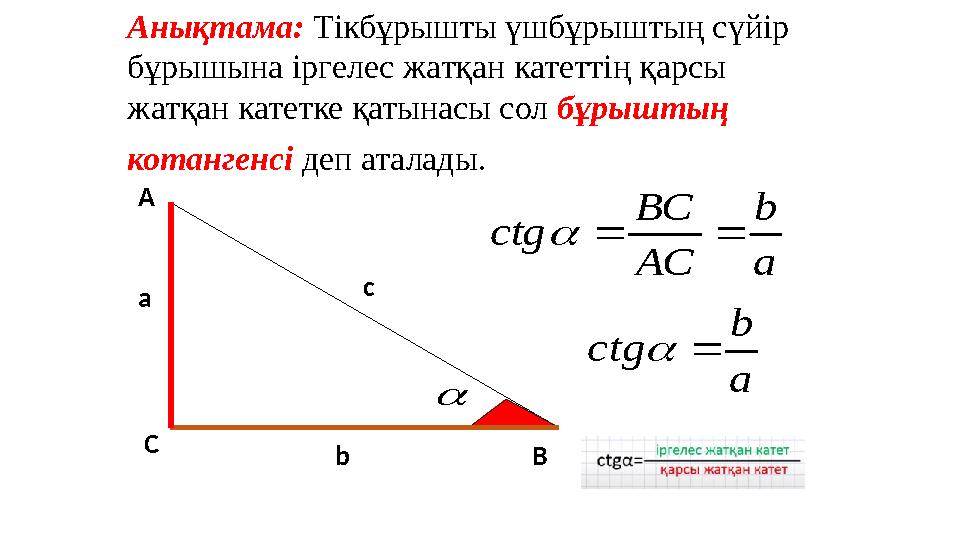
А С Вb c a a b АС ВС ctg  Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің қарсы жатқан катетке қатынасы сол бұрыштың котангенсі деп аталады. a b ctg 

6 слайд

А С Вb c a a b АС ВС ctg  Анықтама: Тікбұрышты үшбұрыштың сүйір бұрышына іргелес жатқан катеттің қарсы жатқан катетке қатынасы сол бұрыштың котангенсі деп аталады. a b ctg 

7 слайд

8 слайд

9 слайд