Открытый урок на тему: Электрический заряд. Закон сохранения электрического заряда.

1 слайд
Электрический заряд. Закон сохранения электрического заряда

1 слайд

2 слайд
1.1. Электрические заряды. Способы получения зарядов. Закон сохранения электрического заряда. 1.2. Взаимодействие электрических зарядов. Закон Кулона. Применение закона Кулона для расчета сил взаимодействия протяженных заряженных тел. 1.3. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей.

2 слайд

3 слайд
Предмет электродинамики. Электродинамика - раздел физики, изучающий поведения электромагнитного поля, осуществляющего взаимодействие между электрическими зарядами. Электростатика – раздел электродинамики, изучающий взаимодействие неподвижных заряженных тел . Электрическое поле, осуществляющее это взаимодействие, называется электростатическим .

3 слайд

4 слайд
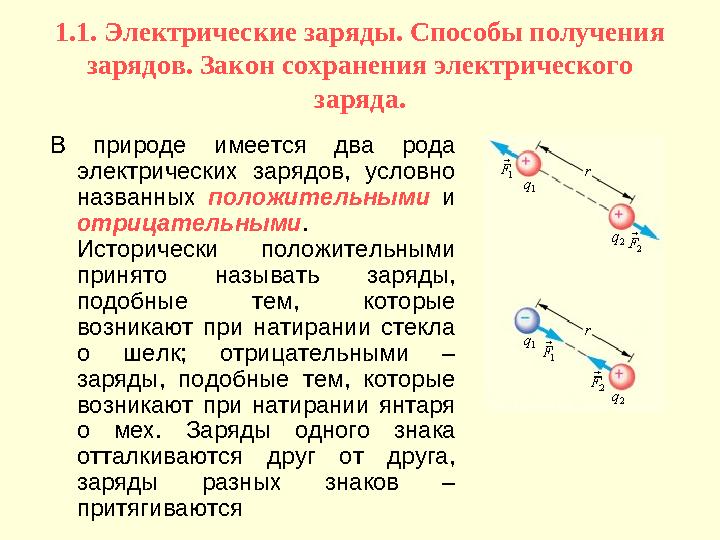
1.1. Электрические заряды. Способы получения зарядов. Закон сохранения электрического заряда. В природе имеется два рода электрических зарядов, условно названных положительными и отрицательными . Исторически положительными принято называть заряды, подобные тем, которые возникают при натирании стекла о шелк; отрицательными – заряды, подобные тем, которые возникают при натирании янтаря о мех. Заряды одного знака отталкиваются друг от друга, заряды разных знаков – притягиваются

4 слайд

5 слайд
По своей сути электрические заряды атомистичны ( дискретны ). Это означает, что в природе существует мельчайший, далее не делимый заряд, получивший название элементарного . Величина элементарного заряда по абсолютной величине в системе СИ: Следует, однако, отметить, что согласно современным представлениям сильновзаимодействующие частицы – адроны (мезоны и барионы) – построены из так называемых кварков – особых частиц, несущих дробный заряд. Некоторые кварки имеют заряд ±2 e /3, а некоторые – ± e /3. В свободном состоянии кварки не наблюдаются . Это позволяет считать, что элементарным зарядом в природе является все же целочисленный заряд е , а не дробный заряд кварков. Заряд макроскопических тел образуется совокупностью элементарных зарядов и является, таким образом, целым кратным е . Кл e 19 10 602,1 | |   

5 слайд

6 слайд
Для проведения опытов с электрическими зарядами используют различные способы их получения. Самый простой и самый древний способ – натирание одних тел другими. Этот способ получения электрических зарядов лежит в основе действия некоторых электрических машин, например, электростатического генератора Ван де Графа ( Van de Graaff R ., 1901-1967 ), применяемого в физике высоких энергий.

6 слайд

7 слайд
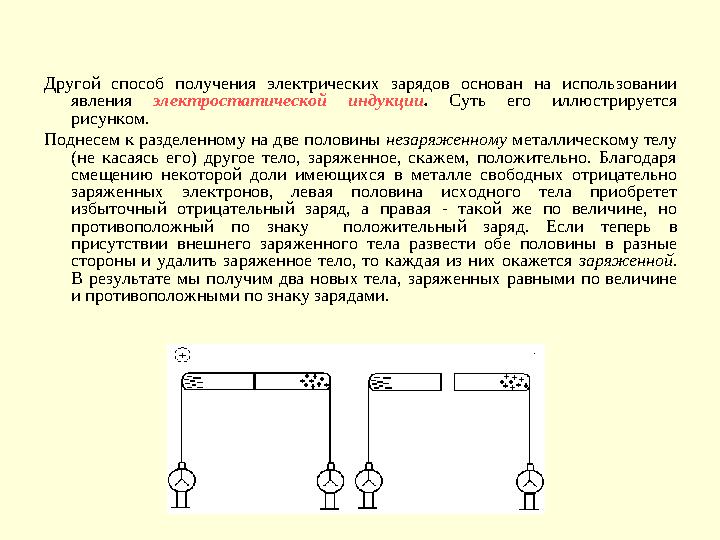
Другой способ получения электрических зарядов основан на использовании явления электростатической индукции . Суть его иллюстрируется рисунком. Поднесем к разделенному на две половины незаряженному металлическому телу (не касаясь его) другое тело, заряженное, скажем, положительно. Благодаря смещению некоторой доли имеющихся в металле свободных отрицательно заряженных электронов, левая половина исходного тела приобретет избыточный отрицательный заряд, а правая - такой же по величине, но противоположный по знаку положительный заряд. Если теперь в присутствии внешнего заряженного тела развести обе половины в разные стороны и удалить заряженное тело, то каждая из них окажется заряженной. В результате мы получим два новых тела, заряженных равными по величине и противоположными по знаку зарядами.

7 слайд

8 слайд
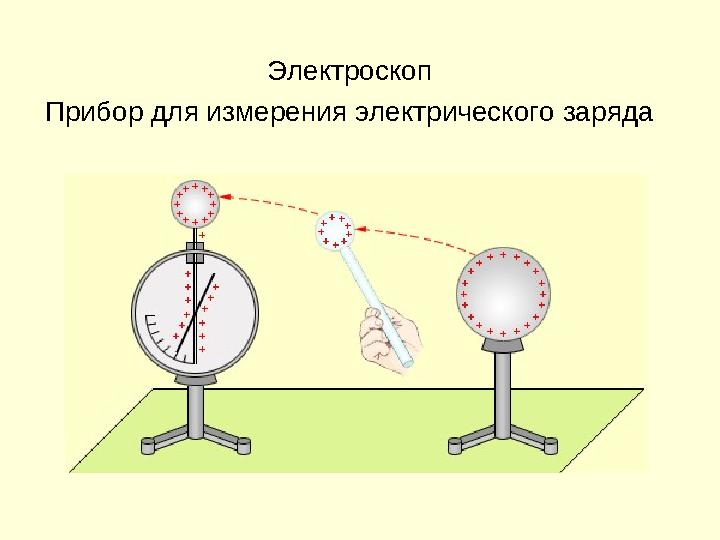
Электроскоп Прибор для измерения электрического заряда

8 слайд

9 слайд
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда . В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной: Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. const q q n i i    1

9 слайд

10 слайд
1.2. Взаимодействие электрических зарядов. Закон Кулона. Применение закона Кулона для расчета сил взаимодействия протяженных заряженных тел

10 слайд

11 слайд
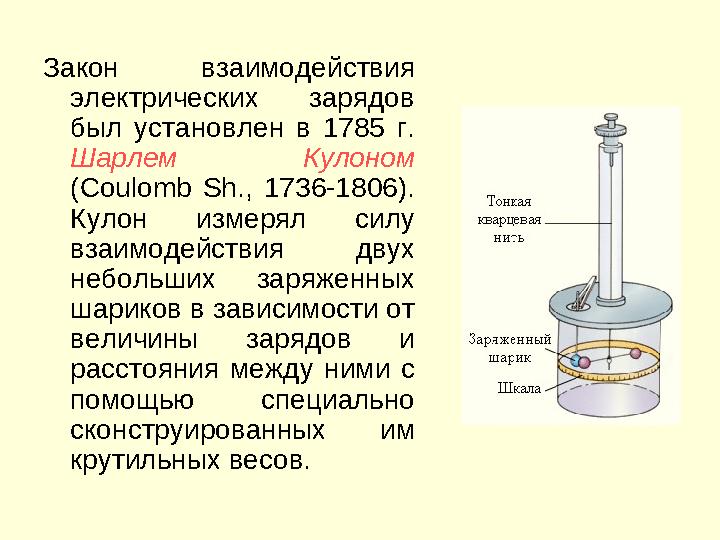
Закон взаимодействия электрических зарядов был установлен в 1785 г. Шарлем Кулоном ( Coulomb Sh ., 1736-1806). Кулон измерял силу взаимодействия двух небольших заряженных шариков в зависимости от величины зарядов и расстояния между ними с помощью специально сконструированных им крутильных весов.

11 слайд

12 слайд
Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов, отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка 10 –9 Н. Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным , то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами . Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь .

12 слайд

13 слайд
В результате своих опытов Кулон установил, что сила взаимодействия двух точечных зарядов прямо пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними, при этом направление действия силы совпадает с прямой, проходящей через оба заряда : Коэффициент пропорциональности k зависит от выбора единиц измерения входящих в эту формулу величин: В Международной системе единиц измерения (СИ) закон Кулона записывается, следовательно, в виде: r r q q k F   3 2 1                  . 1 ] [; 1 ; 1 ; 10 85, 8 ; 4 1 : 12 Н F м r Кл q м Ф k СИ o o   r r q q F   3 0 2 1 4  

13 слайд

14 слайд
В Международной системе СИ за единицу заряда принят кулон (Кл). Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока ( ампер ) в СИ является наряду с единицами длины, времени и массы основной единицей измерения . Заряд электрона в системе СИ равен е = 1,602177·10 –19 Кл ≈ 1,6·10 –19 Кл.

14 слайд

15 слайд
Необходимо подчеркнуть, что в таком виде закон Кулона формулируется только для точечных зарядов , то есть таких заряженных тел, размерами которых можно пренебречь по сравнению с расстоянием между ними. Если это условие не выполняется, то закон Кулона должен быть записан в дифференциальной форме для каждой пары элементарных зарядов dq 1 и dq 2 , на которые «разбиваются» заряженные тела: Тогда полная сила взаимодействия двух макроскопических заряженных тел будет представлена в виде: Интегрирование в этой формуле производится по всем зарядам каждого тела. r r dq dq F d   3 0 2 1 4     2 1 3 2 1 0 4 1 q q r r dq dq F   

15 слайд

16 слайд
Пример . Найти силу F , действующую на точечный заряд Q со стороны бесконечно протяженной прямолинейной заряженной нити. Расстояние от заряда до нити a , линейная плотность заряда нити τ . Искомая сила F = F x = Qτ /(2πε 0 a )                                  0 ) ( 4 2 ) ( 4 ) ( 4 sin, cos sin cos 4 ] [ lim 2 3 2 2 0 0 2 3 2 2 0 2 3 2 2 0 2 2 2 2 2 2 2 2 0 0 y a ydy Q F a Q y a dy a Q y a ady Q F y a y r y y a a r a dF dF dF dF y a r dy dq r Qdq dF м Кл l q y x y x l               

16 слайд

17 слайд
1.3. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей. Взаимодействие электрических зарядов осуществляется через особый вид материи, порождаемой заряженными частицами - электрическое поле . Электрические заряды изменяют свойства окружающего их пространства. Проявляется это в том, что на помещенный вблизи заряженного тела другой заряд (назовем его пробным ) действует сила. По величине этой силы можно судить об «интенсивности» поля, созданного зарядом q . Для того, чтобы сила, действующая на пробный заряд, характеризовала электрическое поле именно в данной точке пространства, пробный заряд, очевидно, должен быть точечным .

17 слайд

18 слайд
Поместив пробный заряд q пр на некотором расстоянии r от заряда q , мы обнаружим, что на него действует сила, величина которой зависит от величины взятого пробного заряда q пр . Легко, однако, видеть, что для всех пробных зарядов отношение F / q пр будет одно и тоже и зависит лишь от величин q и r , определяющих поле заряда q в данной точке r . Естественно, поэтому, принять это отношение за величину, характеризующую «интенсивность» или, как говорят, напряженность электрического поля (в данном случае поля точечного заряда ): 2 0 4 r q q F пр    2 0 4 r q q F E пр   

18 слайд

19 слайд
Таким образом, напряженность электрического поля является его силовой характеристикой . Напряженность поля – вектор . Его направление совпадает с направлением вектора силы , действующей на точечный заряд, помещенный в это поле. Следовательно, если в электрическое поле напряженностью поместить точечный заряд q , то на него будет действовать сила: Размерность напряженности электрического поля в СИ: E q F      м В E 

19 слайд

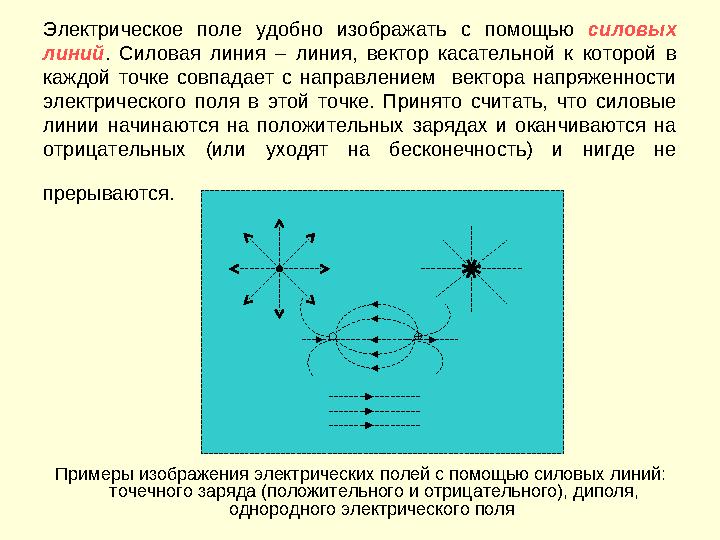
20 слайд
Электрическое поле удобно изображать с помощью силовых линий . Силовая линия – линия, вектор касательной к которой в каждой точке совпадает с направлением вектора напряженности электрического поля в этой точке. Принято считать, что силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность) и нигде не прерываются. Примеры изображения электрических полей с помощью силовых линий: точечного заряда (положительного и отрицательного), диполя, однородного электрического поля

20 слайд

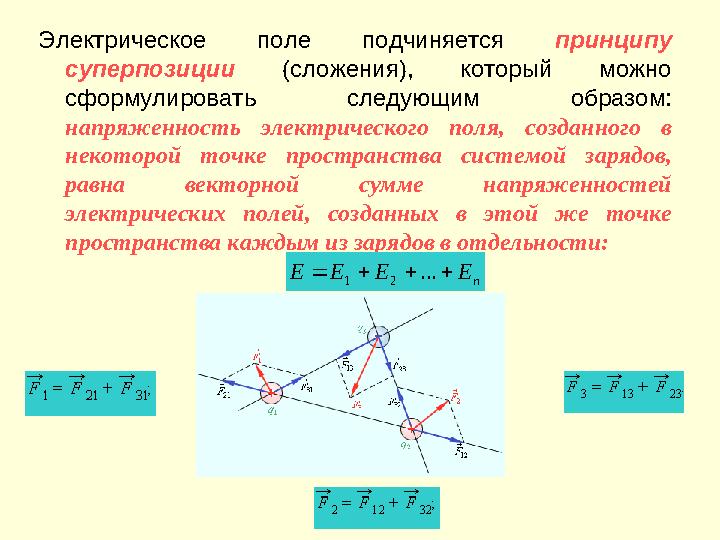
21 слайд
Электрическое поле подчиняется принципу суперпозиции (сложения), который можно сформулировать следующим образом: напряженность электрического поля, созданного в некоторой точке пространства системой зарядов, равна векторной сумме напряженностей электрических полей, созданных в этой же точке пространства каждым из зарядов в отдельности:n E E E E         ... 2 1

21 слайд