Представление данных. Тема 1. Системы счисления». «Тема 2. Логические основы компьютера».





1 слайд
Тема урока: «Раздел 2.
Представление данных. Тема 1.
Системы счисления». « Тема 2.
Логические основы
компьютера».
Цель : объяснить понятие представление данных , системы
счисления; познакомить с разными системами счисления;
- дать понятие о системе счисления;
- о видах систем счисления;
- об особенностях двоичной системы счисления;
- о переводе чисел из десятичной системы счисления в
двоичную, восьме р ичную и шестнадцатеричную.
1 слайд
Тема урока: «Раздел 2. Представление данных. Тема 1. Системы счисления». « Тема 2. Логические основы компьютера». Цель : объяснить понятие представление данных , системы счисления; познакомить с разными системами счисления; - дать понятие о системе счисления; - о видах систем счисления; - об особенностях двоичной системы счисления; - о переводе чисел из десятичной системы счисления в двоичную, восьме р ичную и шестнадцатеричную.

2 слайд
Критерии оценки:
95-100
Отлично
п ереводить целые числа из десятичной системы
счисления в двоичную, восьмеричную,
шестнадцатеричную и обратно.
0-49
Неудовлетворительно
Не переводить целые числа из десятичной системы счисления в
двоичную, восьмеричную , шестнадцатеричную не переводить и
обратно .
2 слайд
Критерии оценки: 95-100 Отлично п ереводить целые числа из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и обратно. 0-49 Неудовлетворительно Не переводить целые числа из десятичной системы счисления в двоичную, восьмеричную , шестнадцатеричную не переводить и обратно .

3 слайд
вопросы:
1. в какой сфере применяется систем а счисления?
2. к ак можно перевести числа из десятичной системы
счисления в любую другую?
3. к ак можно перевести числа из двоичной системы
счисления в любую другую?
4. почему персональный компьютер работает с
кодом, написанным в двоичной системе
счисления?
5. почему в вычислительной технике используются
только цифры 0 и 1?
6. любое ли число можно перевести в двоичную
систему?
3 слайд
вопросы: 1. в какой сфере применяется систем а счисления? 2. к ак можно перевести числа из десятичной системы счисления в любую другую? 3. к ак можно перевести числа из двоичной системы счисления в любую другую? 4. почему персональный компьютер работает с кодом, написанным в двоичной системе счисления? 5. почему в вычислительной технике используются только цифры 0 и 1? 6. любое ли число можно перевести в двоичную систему?

4 слайд
История
В 1666 году В. Лейбниц предложил идею
записи любого числа в двоичной системе и
возможность использовать двоичную систему
в вычислительном устройстве.
Все виды информации, хранящиеся в памяти
компьютера (слова, числа, рисунки,
программы управления работой компьютера),
записываются в виде последовательности
двоичных чисел. В вычислительной технике
двоичные числовые символы 0 и 1
называются специальным термином - бит ,
который является единицей измерения
информации.
4 слайд
История В 1666 году В. Лейбниц предложил идею записи любого числа в двоичной системе и возможность использовать двоичную систему в вычислительном устройстве. Все виды информации, хранящиеся в памяти компьютера (слова, числа, рисунки, программы управления работой компьютера), записываются в виде последовательности двоичных чисел. В вычислительной технике двоичные числовые символы 0 и 1 называются специальным термином - бит , который является единицей измерения информации.

5 слайд
Система счисления?
Система счисления - это совокупность правил
записи чисел и арифметических операций над
ними. Системы счисления делятся на позиционные
и непозиционные.
В непозиционной системе счисления цифры не
зависят от значения (мощности) числа, от
положения (позиции). В каче¬стве примера можно
привести римские цифры, которые пишутся с
использо¬ванием латинского алфавита: CCLXVII
(100+100+50+10+7). Здесь С - число сто, где бы оно
не стояло, L - пятьдесят и т.д.
5 слайд
Система счисления? Система счисления - это совокупность правил записи чисел и арифметических операций над ними. Системы счисления делятся на позиционные и непозиционные. В непозиционной системе счисления цифры не зависят от значения (мощности) числа, от положения (позиции). В каче¬стве примера можно привести римские цифры, которые пишутся с использо¬ванием латинского алфавита: CCLXVII (100+100+50+10+7). Здесь С - число сто, где бы оно не стояло, L - пятьдесят и т.д.

6 слайд
позиционная система
счисления
В позиционной системе счисления значение
каждой цифры зависит от ее положения,
например, в числе 777,7 первая цифра 7 –
сот десятков, 4 из разряда единиц.
6 слайд
позиционная система счисления В позиционной системе счисления значение каждой цифры зависит от ее положения, например, в числе 777,7 первая цифра 7 – сот десятков, 4 из разряда единиц.

7 слайд
Десятичная система счисления
Десятичная система счисления является позиционной, так
как в записи десятичного числа зна чение цифры зависит от
его позиции или от его места в чис ле . Позицию,
выделенную на цифру числа, называют разрядом.
Если записать число 234 в виде суммы, то получим следу
ющее: 2*10 2
+ 3*10 J
+ 4*10 0
. Число 10 в этой записи
я в л яю тся основанием системы счисления. Для каждой
цифры чис 1а 10 в зависимости от позиции цифры
основания возводится в сте
пень и умножается на эту цифру.
Для единиц - 0; для деся
тичных знаков - 1, для сотен - 2 и
так далее
7 слайд
Десятичная система счисления Десятичная система счисления является позиционной, так как в записи десятичного числа зна чение цифры зависит от его позиции или от его места в чис ле . Позицию, выделенную на цифру числа, называют разрядом. Если записать число 234 в виде суммы, то получим следу ющее: 2*10 2 + 3*10 J + 4*10 0 . Число 10 в этой записи я в л яю тся основанием системы счисления. Для каждой цифры чис 1а 10 в зависимости от позиции цифры основания возводится в сте пень и умножается на эту цифру. Для единиц - 0; для деся тичных знаков - 1, для сотен - 2 и так далее

8 слайд
Двоичная система счисления
Двоичная система счисления - позиционная
система счисления с основанием числа 2 . В
этой системе счисления используются только
два знака - 0 и 1 . Каждая единица
следующего разряда будет в 2 раза больше
предыдущей, следовательно, эти единицы
образуют последовательность чисел 2, 4, 8,
16, ..., 2 n
8 слайд
Двоичная система счисления Двоичная система счисления - позиционная система счисления с основанием числа 2 . В этой системе счисления используются только два знака - 0 и 1 . Каждая единица следующего разряда будет в 2 раза больше предыдущей, следовательно, эти единицы образуют последовательность чисел 2, 4, 8, 16, ..., 2 n

9 слайд
Правило №1. Перевод чисел (2)
→ (8), (2) → (16) (написать конспект)
Чтобы перевести число из двоичной
системы в восьмеричную или
шестнадцатеричную, его нужно разбить
влево и вправо от запятой на триады (для
восьмеричной) или тетрады (для
шестнадцатеричной) и каждую такую группу
заменить соответствующей восьмеричной
(шестнадцатеричной) цифрой.
9 слайд
Правило №1. Перевод чисел (2) → (8), (2) → (16) (написать конспект) Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.

10 слайд
Напишите в тетрадь примеры
Примеры:
1101010000111
2 = 1 5 2 0 7
8 ;
1 101 010 000 111
110111000001101
2 = 6 E 0 D
16
110 1110 0000 1101
10 слайд
Напишите в тетрадь примеры Примеры: 1101010000111 2 = 1 5 2 0 7 8 ; 1 101 010 000 111 110111000001101 2 = 6 E 0 D 16 110 1110 0000 1101

11 слайд
Восьмеричная система
счисления (написать в тетради)
Восьмеричная система счисления - позиционная
целочисленная система счисления с основанием 8.
Для представления чисел в ней использую т с я
цифры от 0 до 7. Например, число 356 в
восьмеричной системе записывается так:
356=3*8 2
+5*8+6*8 0
.
11 слайд
Восьмеричная система счисления (написать в тетради) Восьмеричная система счисления - позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней использую т с я цифры от 0 до 7. Например, число 356 в восьмеричной системе записывается так: 356=3*8 2 +5*8+6*8 0 .

12 слайд
Восьмеричная система
счисления (написать в тетради)
Правило №2. Перевод чисел (8) → (2), (16) → (2)
Перевод восьмеричных и шестнадцатеричных чисел в
двоичную систему: каждую цифру заменить
эквивалентной ей двоичной триадой (тройкой цифр) или
тетрадой (четверкой цифр).
Примеры:
5371
8 = 101 011 111 001
2 ;
5 3 7 1
1A3F
16 = 1 1010 0011 1111
2
1 A 3 F
12 слайд
Восьмеричная система счисления (написать в тетради) Правило №2. Перевод чисел (8) → (2), (16) → (2) Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему: каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). Примеры: 5371 8 = 101 011 111 001 2 ; 5 3 7 1 1A3F 16 = 1 1010 0011 1111 2 1 A 3 F

13 слайд
Шестнадцатеричная система
счисления (написать в тетради)
Шестнадцатеричная система счисления - позиционная
система счисления по целочисленному основанию 16. В шест
надцатеричной системе счисления используются цифры от 0
до 9 и шесть первых латинских букв - A (10), B (11), C (12),
D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное первое
разбивается на группы по четыре разряда, начиная с конца. В
случае, если количество разрядов не делится нацело, то к
первой четверке впереди дописываются нули. Каждой
четверке соответствует цифра шестнадцатеричной системы
счисления.
13 слайд
Шестнадцатеричная система счисления (написать в тетради) Шестнадцатеричная система счисления - позиционная система счисления по целочисленному основанию 16. В шест надцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв - A (10), B (11), C (12), D (13), E (14), F (15). При переводе двоичного числа в шестнадцатеричное первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то к первой четверке впереди дописываются нули. Каждой четверке соответствует цифра шестнадцатеричной системы счисления.

14 слайд
Правило
Для того, чтобы перевести число из десятичной
системы счис ления в любую другую , нужно
выполнять целочисленное деление исходного
числа на основание той системы счисления , в
которую нужно перевести число. При этом
важен остаток от деления и частное. Частное
нужно делить на основание до тех пор, пока не
останется 0.
14 слайд
Правило Для того, чтобы перевести число из десятичной системы счис ления в любую другую , нужно выполнять целочисленное деление исходного числа на основание той системы счисления , в которую нужно перевести число. При этом важен остаток от деления и частное. Частное нужно делить на основание до тех пор, пока не останется 0.

15 слайд
Правило №3. Перевод чисел (q)
→ (10)
Правило №3. Перевод чисел (q) → (10)
Запись числа в развернутой форме и вычисление
полученного выражения в десятичной системе.
Примеры:
1. 110110
2 = 1 2∙ 5
+ 1 2 ∙ 4
+ 0 2 ∙ 3
+ 1 2 ∙ 2
+ 1 2 ∙ 1
+ 0 2 ∙ 0
= 54
10 ;
2. 237
8 = 2 8
∙ 2
+ 3 8 ∙ 1
+ 7 8 ∙ 0
= 128 + 24 + 7 = 159
10 ;
3. 3FA
16 = 3 16
∙ 2
+ 15 16 ∙ 1
+ 10 16 ∙ 0
= 768 + 240 + 10 =
1018
10 .
15 слайд
Правило №3. Перевод чисел (q) → (10) Правило №3. Перевод чисел (q) → (10) Запись числа в развернутой форме и вычисление полученного выражения в десятичной системе. Примеры: 1. 110110 2 = 1 2∙ 5 + 1 2 ∙ 4 + 0 2 ∙ 3 + 1 2 ∙ 2 + 1 2 ∙ 1 + 0 2 ∙ 0 = 54 10 ; 2. 237 8 = 2 8 ∙ 2 + 3 8 ∙ 1 + 7 8 ∙ 0 = 128 + 24 + 7 = 159 10 ; 3. 3FA 16 = 3 16 ∙ 2 + 15 16 ∙ 1 + 10 16 ∙ 0 = 768 + 240 + 10 = 1018 10 .

16 слайд
Правило 2.
•
В десятичной системе счисления для выражения
чисел используются арабские цифры от 0 до 9:
0,1, 2, 3, 4, 5, 6, 7, 8, 9. Например: 234 = 200 + 30 +
4, 2 из разряда сотен, 3 из разряда
• Правило 2. Например: 37
10 = ?
2
16 слайд
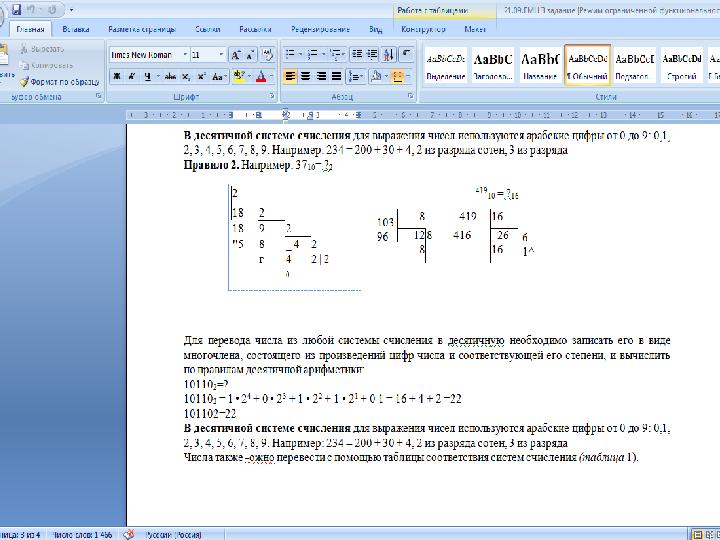
Правило 2. • В десятичной системе счисления для выражения чисел используются арабские цифры от 0 до 9: 0,1, 2, 3, 4, 5, 6, 7, 8, 9. Например: 234 = 200 + 30 + 4, 2 из разряда сотен, 3 из разряда • Правило 2. Например: 37 10 = ? 2
17 слайд
17 слайд

18 слайд
Правило
Для перевода числа из любой системы счисления
в десятичную необходимо записать его в виде
многочлена , состоящего из произведений цифр
числа и соответствующей его степени, и вычислить
по правилам десятичной арифметики:
10110
2 =?
10110
2 = 1 • 2 4
+ 0 • 2 3
+ 1 • 2 2
+ 1 • 2 1
+ 0 1 = 16 + 4 +
2 =22
101102=22
18 слайд
Правило Для перевода числа из любой системы счисления в десятичную необходимо записать его в виде многочлена , состоящего из произведений цифр числа и соответствующей его степени, и вычислить по правилам десятичной арифметики: 10110 2 =? 10110 2 = 1 • 2 4 + 0 • 2 3 + 1 • 2 2 + 1 • 2 1 + 0 1 = 16 + 4 + 2 =22 101102=22

19 слайд
В десятичной системе
счисления
В десятичной системе счисления для выражения
чисел используются арабские цифры от 0 до 9: 0,1,
2, 3, 4, 5, 6, 7, 8, 9. Например: 234 = 200 + 30 + 4, 2 из
разряда сотен, 3 из разряда
Числа также можно перевести с помощью таблицы
соответствия систем счисления:
В таблицы видно, что число 1011
2 в двоичной
системе счисления равно числу 11
10 в десятичной
системе счисления
19 слайд
В десятичной системе счисления В десятичной системе счисления для выражения чисел используются арабские цифры от 0 до 9: 0,1, 2, 3, 4, 5, 6, 7, 8, 9. Например: 234 = 200 + 30 + 4, 2 из разряда сотен, 3 из разряда Числа также можно перевести с помощью таблицы соответствия систем счисления: В таблицы видно, что число 1011 2 в двоичной системе счисления равно числу 11 10 в десятичной системе счисления
20 слайд
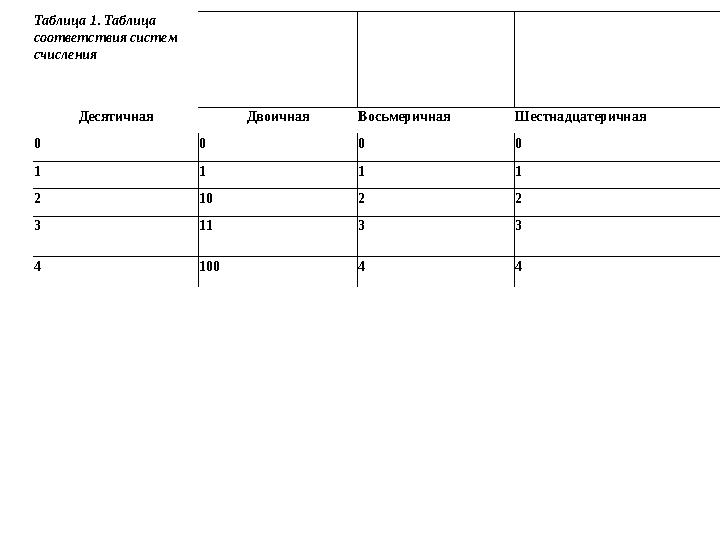
Таблица 1. Таблица
соответствия систем
счисления
Систем счисления
Десятичная Двоичная Восьмеричная Шестнадцатеричная
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
20 слайд
Таблица 1. Таблица соответствия систем счисления Систем счисления Десятичная Двоичная Восьмеричная Шестнадцатеричная 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4
21 слайд
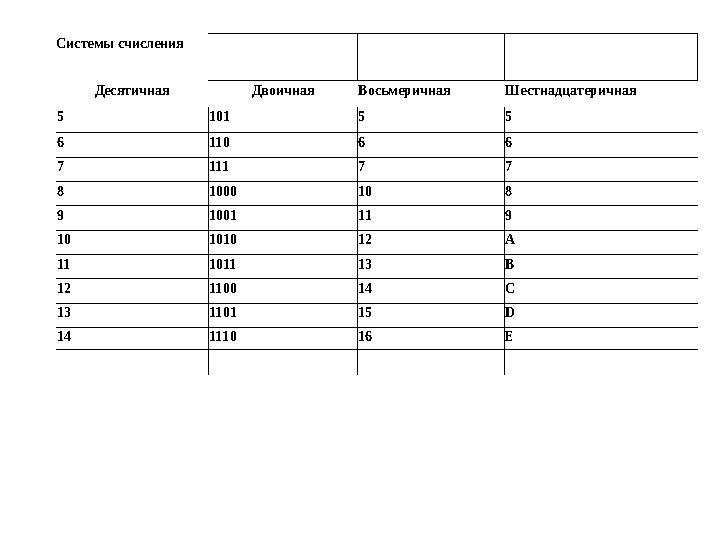
Систем ы счисления
Десятичная Двоичная Восьмеричная Шестнадцатеричная
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
21 слайд
Систем ы счисления Десятичная Двоичная Восьмеричная Шестнадцатеричная 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E

22 слайд
Правило №4. Перевод чисел (q)
→ (10)
Правило №4. Перевод чисел (q) → (10)
Запись числа в развернутой форме и вычисление
полученного выражения в десятичной системе.
Примеры:
1. 110110
2 = 1 2∙ 5
+ 1 2 ∙ 4
+ 0 2 ∙ 3
+ 1 2 ∙ 2
+ 1 2 ∙ 1
+ 0 2 ∙ 0
=
54
10 ;
2. 237
8 = 2 8
∙ 2
+ 3 8 ∙ 1
+ 7 8 ∙ 0
= 128 + 24 + 7 = 159
10 ;
3. 3FA
16 = 3 16
∙ 2
+ 15 16 ∙ 1
+ 10 16 ∙ 0
= 768 + 240 + 10 =
1018
10 .
22 слайд
Правило №4. Перевод чисел (q) → (10) Правило №4. Перевод чисел (q) → (10) Запись числа в развернутой форме и вычисление полученного выражения в десятичной системе. Примеры: 1. 110110 2 = 1 2∙ 5 + 1 2 ∙ 4 + 0 2 ∙ 3 + 1 2 ∙ 2 + 1 2 ∙ 1 + 0 2 ∙ 0 = 54 10 ; 2. 237 8 = 2 8 ∙ 2 + 3 8 ∙ 1 + 7 8 ∙ 0 = 128 + 24 + 7 = 159 10 ; 3. 3FA 16 = 3 16 ∙ 2 + 15 16 ∙ 1 + 10 16 ∙ 0 = 768 + 240 + 10 = 1018 10 .

23 слайд
Контрольные вопросы
Контрольные вопросы:
в какой сфере применяется систем а счисления?
к ак можно перевести числа из десятичной системы
счисления в любую другую?
к ак можно перевести числа из двоичной системы
счисления в любую другую?
4. почему персональный компьютер работает с
кодом, написанным в двоичной системе счисления?
5. почему в вычислительной технике
используются только цифры 0 и 1?
6. любое ли число можно перевести в двоичную
систему?
23 слайд
Контрольные вопросы Контрольные вопросы: в какой сфере применяется систем а счисления? к ак можно перевести числа из десятичной системы счисления в любую другую? к ак можно перевести числа из двоичной системы счисления в любую другую? 4. почему персональный компьютер работает с кодом, написанным в двоичной системе счисления? 5. почему в вычислительной технике используются только цифры 0 и 1? 6. любое ли число можно перевести в двоичную систему?

24 слайд
Домашнее задание:
Задание №2. Используя лекционный материал и Интернет сделать анализ:
сравните двоичную и десятичную системы счисления определите их ра зличия.
Задание №3.
Правило 1 . Для перевода числа из любой системы счисления в деся тичную
необходимо записать его в виде многочлена, состоящего из произведений цифр
числа и соответствующей его степени, и вычислить по правилам десятичной
арифметики:
10110
2 =?
10110
2 = 1 • 2 4
+ 0 • 2 3
+ 1 • 2 2
+ 1 • 2 1
+ 0 1 = 16 + 4 + 2 =22
101102=22
Используя это правило 1 и таблицу 1 решить задачи: 1 ) 1110
2 = ?
10 2) 1111
2 = ?
10
3) 103
10 = ?
8 4) 419
10 =?
16
Задание №4. Используя правило №2, правило №3, правило №4 п еревести
следующие числа в указанную систему счисления:
а) 23
1 0 Х
2 ; б) 1248
1 0 Х
16 ; 8462
1 0 Х
8;
в) 10100011
2 Х
10 ;
24 слайд
Домашнее задание: Задание №2. Используя лекционный материал и Интернет сделать анализ: сравните двоичную и десятичную системы счисления определите их ра зличия. Задание №3. Правило 1 . Для перевода числа из любой системы счисления в деся тичную необходимо записать его в виде многочлена, состоящего из произведений цифр числа и соответствующей его степени, и вычислить по правилам десятичной арифметики: 10110 2 =? 10110 2 = 1 • 2 4 + 0 • 2 3 + 1 • 2 2 + 1 • 2 1 + 0 1 = 16 + 4 + 2 =22 101102=22 Используя это правило 1 и таблицу 1 решить задачи: 1 ) 1110 2 = ? 10 2) 1111 2 = ? 10 3) 103 10 = ? 8 4) 419 10 =? 16 Задание №4. Используя правило №2, правило №3, правило №4 п еревести следующие числа в указанную систему счисления: а) 23 1 0 Х 2 ; б) 1248 1 0 Х 16 ; 8462 1 0 Х 8; в) 10100011 2 Х 10 ;

25 слайд
Тема урока: « Тема 2. Логические
основы компьютера»
Цель : объяснить понятие логические основы компьютера;
п реобразо вание логически х выражени и в логические схемы и
наоборот.
Критерий оценивания
Оценка «А-»
90-94 балл
1) о бъясняет понятие логические основы компьютера с
малейшими ошибками : конъюнктор, дизъюнктор,
инвертор;
2) п реобразовывает логические выражения в логические
схемы и наоборот.
25 слайд
Тема урока: « Тема 2. Логические основы компьютера» Цель : объяснить понятие логические основы компьютера; п реобразо вание логически х выражени и в логические схемы и наоборот. Критерий оценивания Оценка «А-» 90-94 балл 1) о бъясняет понятие логические основы компьютера с малейшими ошибками : конъюнктор, дизъюнктор, инвертор; 2) п реобразовывает логические выражения в логические схемы и наоборот.

26 слайд
Что такое логика?
Логика - это наука о видах и законах
человеческого мышления, в том числе о
закономерностях высказываний, которые можно
доказать. Как научные дисциплины
сформированы формальная, математическая,
вероятностная и др. виды логики.
26 слайд
Что такое логика? Логика - это наука о видах и законах человеческого мышления, в том числе о закономерностях высказываний, которые можно доказать. Как научные дисциплины сформированы формальная, математическая, вероятностная и др. виды логики.

27 слайд
Формальная логика
Формальная логика - это логика, связанная с
анализом нашего содержательного мнения,
которое выражается языком речи.
27 слайд
Формальная логика Формальная логика - это логика, связанная с анализом нашего содержательного мнения, которое выражается языком речи.

28 слайд
Вероятностная логика
- логика, созда ваемая случайными
параметрами, основан
ная на
использовании нескольких серий
испытаний.
28 слайд
Вероятностная логика - логика, созда ваемая случайными параметрами, основан ная на использовании нескольких серий испытаний.

29 слайд
Математическая логика
Математическая логика является частью
формальной логики, имеет четко опреде
ленные формы и высказывания. Она изуча
ют
только те мысли, которые можно решить их
истинность или ложь.
29 слайд
Математическая логика Математическая логика является частью формальной логики, имеет четко опреде ленные формы и высказывания. Она изуча ют только те мысли, которые можно решить их истинность или ложь.

30 слайд
Высказывание
Высказывание - какое-либо предположение,
которое может быть истиной или ложью.
Например, высказывания «Нур-Султан - столица
Республики Казахстан» и «2 * 3 = 6» - истинные, а
такие, как «гораплоская», «2*2 = 5»- ложные.
В математике логические союзы являются
логическими операциями, описывающими
сложные утверждения.
Для работы с логическими утверждениями им
присваивают имя.
30 слайд
Высказывание Высказывание - какое-либо предположение, которое может быть истиной или ложью. Например, высказывания «Нур-Султан - столица Республики Казахстан» и «2 * 3 = 6» - истинные, а такие, как «гораплоская», «2*2 = 5»- ложные. В математике логические союзы являются логическими операциями, описывающими сложные утверждения. Для работы с логическими утверждениями им присваивают имя.

31 слайд
история
Алгебра логики впервые появилась в XIX
веке в работах английского математика
Джорджа Буля. Это был результат
стремления к решению традиционных
логических задач алгебраическими
методами.
31 слайд
история Алгебра логики впервые появилась в XIX веке в работах английского математика Джорджа Буля. Это был результат стремления к решению традиционных логических задач алгебраическими методами.

32 слайд
логические операции И, ИЛИ,
НЕ
В математической логике есть такие логические
операции И, ИЛИ, НЕ и они определяются
таблицей истинности.
Таблица истинности - это предста вл ени е
логических операций в виде таблицы, в которой
все возможные последовательности значений
истинности встроенных операнд перечислены
вместе с фактическим значением результата
операции для каждой из этих
последовательностей .
32 слайд
логические операции И, ИЛИ, НЕ В математической логике есть такие логические операции И, ИЛИ, НЕ и они определяются таблицей истинности. Таблица истинности - это предста вл ени е логических операций в виде таблицы, в которой все возможные последовательности значений истинности встроенных операнд перечислены вместе с фактическим значением результата операции для каждой из этих последовательностей .

33 слайд
Правила №1. Логическое
умножение (конъюнкц и я)
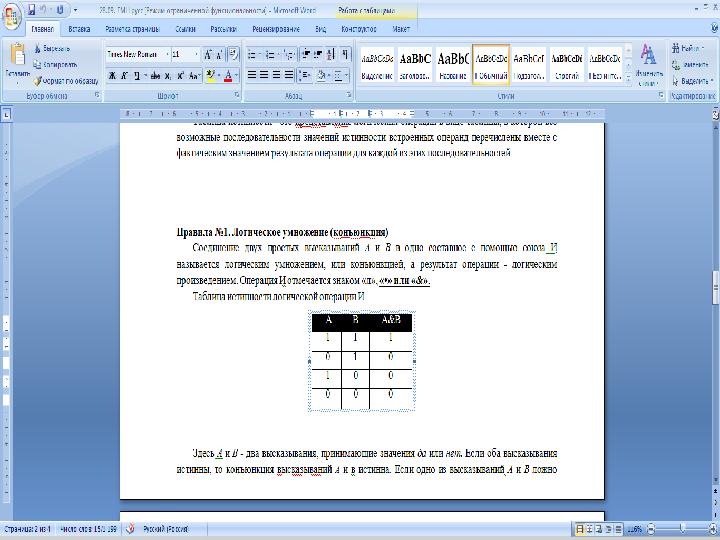
Правила №1. Логическое умножение (конъюнкц и я)
Соединение двух простых высказываний A и B в одно
составное с помощью союза И называется логическим
умножением, или конъюнкцией , а результат операции -
логическим произведением . Операция И отмечается
знаком «л», «•» или «&».
Таблица истинности логической операции И.
Здесь А и В - два высказывания, принимающие значения
да или нет. Если оба высказывания истинны, то
конъюнкция высказыван и й А и в истинна. Если одно из
высказываний А и В ложно или оба высказывания ложны,
то конъюнкция А и В ложна.
33 слайд
Правила №1. Логическое умножение (конъюнкц и я) Правила №1. Логическое умножение (конъюнкц и я) Соединение двух простых высказываний A и B в одно составное с помощью союза И называется логическим умножением, или конъюнкцией , а результат операции - логическим произведением . Операция И отмечается знаком «л», «•» или «&». Таблица истинности логической операции И. Здесь А и В - два высказывания, принимающие значения да или нет. Если оба высказывания истинны, то конъюнкция высказыван и й А и в истинна. Если одно из высказываний А и В ложно или оба высказывания ложны, то конъюнкция А и В ложна.
34 слайд
34 слайд

35 слайд
Правила №2. Логическое
сложение (дизъюнкция)
Правила №2. Логическое сложение (дизъюнкция)
Объединение двух простых утверждений A и B в одно
составное утверждение с помощью союза ИЛИ называется
логическим сложением , или дизъюнкцие й, а результат
« v » или «+».
Таблица истинности логической операции ИЛИ.
Если одно из высказываний А и В истинно, т о д и зъюнкция
А и В будет истинной. Если же оба высказывания А и В
ложны, то дизъюнкция А и В ложна.
35 слайд
Правила №2. Логическое сложение (дизъюнкция) Правила №2. Логическое сложение (дизъюнкция) Объединение двух простых утверждений A и B в одно составное утверждение с помощью союза ИЛИ называется логическим сложением , или дизъюнкцие й, а результат « v » или «+». Таблица истинности логической операции ИЛИ. Если одно из высказываний А и В истинно, т о д и зъюнкция А и В будет истинной. Если же оба высказывания А и В ложны, то дизъюнкция А и В ложна.

36 слайд
Правила №3. Логическое
отрицание (инверсия)
Правила №3. Логическое отрицание (инверсия)
Присвоение союза НЕ простому утверждению A
называется логическим отрицанием , или
инверсией, в результате выполнения этой
операции появляется новое утверждение.
Операция НЕ обозначается чертой над
утверждением А или знаком «-». Таблица
истинности логической операции НЕ.
Если исходное высказывание ложно, тогда
отрицание является истинным, и наоборот, если
исходное высказывание истинно, то его
отр иц ание ложно.
36 слайд
Правила №3. Логическое отрицание (инверсия) Правила №3. Логическое отрицание (инверсия) Присвоение союза НЕ простому утверждению A называется логическим отрицанием , или инверсией, в результате выполнения этой операции появляется новое утверждение. Операция НЕ обозначается чертой над утверждением А или знаком «-». Таблица истинности логической операции НЕ. Если исходное высказывание ложно, тогда отрицание является истинным, и наоборот, если исходное высказывание истинно, то его отр иц ание ложно.
37 слайд
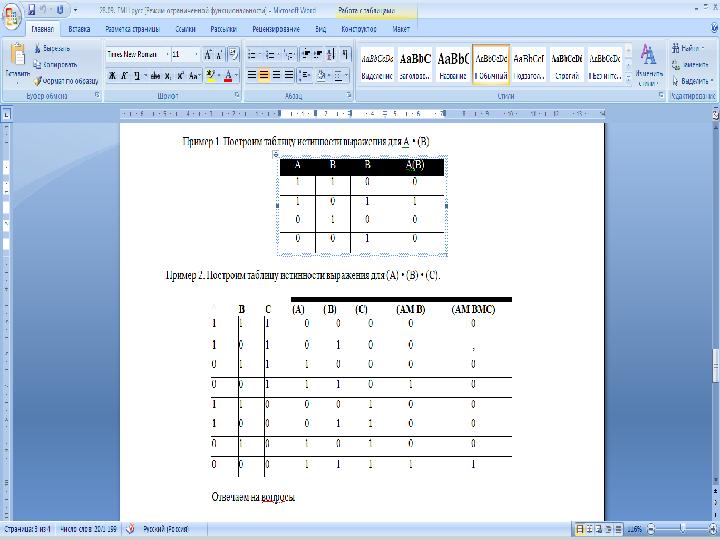
Пример 1.
Пример 1. Построим таблицу истинности выражения для А
• (В).
37 слайд
Пример 1. Пример 1. Построим таблицу истинности выражения для А • (В).

38 слайд
Пример 2.
Пример 2. Построим таблицу
истинности выражения для ( A ) • (В) •
( C ).
38 слайд
Пример 2. Пример 2. Построим таблицу истинности выражения для ( A ) • (В) • ( C ).

39 слайд
Контрольные вопросы:
Отвечаем на вопро с ы
1.Что такое логика?
2.Какова роль логики в повседневной жизни?
3.В чем разница между вероятностной и формальной
логикой?
4.Зачем используются логические операции?
5.Каков порядок выполнения логических операций?
6.Для чего используются высказывания?
39 слайд
Контрольные вопросы: Отвечаем на вопро с ы 1.Что такое логика? 2.Какова роль логики в повседневной жизни? 3.В чем разница между вероятностной и формальной логикой? 4.Зачем используются логические операции? 5.Каков порядок выполнения логических операций? 6.Для чего используются высказывания?

40 слайд
Домашнее задание:
Задание №3. Постройте таблицы истинности для следующих логиче ских
выражений.
F(x1, x2, x3) = x3 v (x2 & x1 & x3)
F(x1, x2, x3) = x1 & x2 v x2 v x1 & x3
F(x1, x2, x3) = x1 & x2 & x3 v x1 v x2 v x3
Задание №4. Используя лекционный материал и Интернет сделать
анализ:
о т чего зависит формальная логика?
д ля чего нужна вероятностная логика?
к акие существуют связи между математической и фор
мальной логикой?
д ля чего в информатике нужны логические операции И, ИЛИ, НЕ?
40 слайд
Домашнее задание: Задание №3. Постройте таблицы истинности для следующих логиче ских выражений. F(x1, x2, x3) = x3 v (x2 & x1 & x3) F(x1, x2, x3) = x1 & x2 v x2 v x1 & x3 F(x1, x2, x3) = x1 & x2 & x3 v x1 v x2 v x3 Задание №4. Используя лекционный материал и Интернет сделать анализ: о т чего зависит формальная логика? д ля чего нужна вероятностная логика? к акие существуют связи между математической и фор мальной логикой? д ля чего в информатике нужны логические операции И, ИЛИ, НЕ?















