Материалдар / Презентация "Функция графигінің асимптоталары" 10 сынып

Презентация "Функция графигінің асимптоталары" 10 сынып

Материал туралы қысқаша түсінік

Жаңа тақырыпты өткенде көп көмегі тиеді

Карыбаева Сауле Шешкеновна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

13 Маусым 2018

3031

23 рет жүктелген

Алгебра Презентация 10 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 6

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
L/O/G/O Функция Функция графигінің графигінің асимптоталарыасимптоталары Функция Функция графигінің графигінің асимптоталарыасимптоталары CC абақтың абақтың : тақырыбы : тақырыбы

1 слайд

L/O/G/O Функция Функция графигінің графигінің асимптоталарыасимптоталары Функция Функция графигінің графигінің асимптоталарыасимптоталары CC абақтың абақтың : тақырыбы : тақырыбы

2 слайд
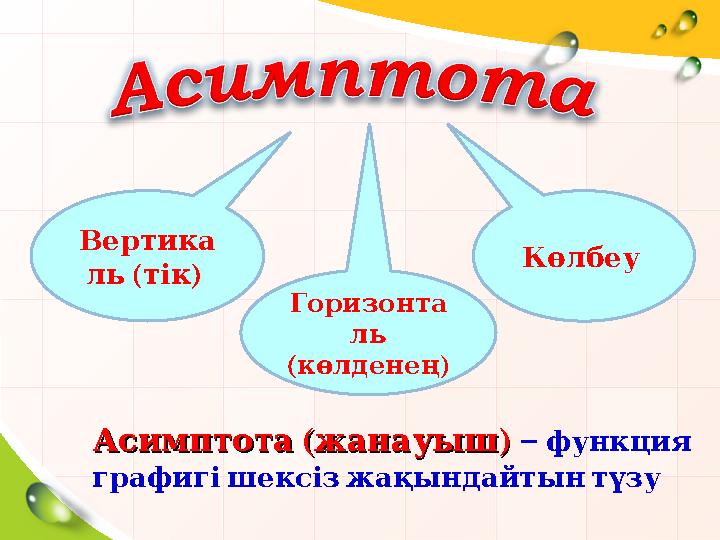
Көлбеу Горизонта ль ( ) көлденең Вертика ( ) ль тік ( ) Асимптота жанауыш ( ) Асимптота жанауыш – функция графигішексізжақындайтынтүзу

2 слайд

Көлбеу Горизонта ль ( ) көлденең Вертика ( ) ль тік ( ) Асимптота жанауыш ( ) Асимптота жанауыш – функция графигішексізжақындайтынтүзу

3 слайд
2  2     2 3 2 3  x y 0 tgxy функциясы Вертикаль ( ) тік асимптотасыбар 2 3 ; 2 3 ; 2 ; 2   xxxx Znnx  , 2   Жалпытеңдеуі түзуі tgxlim 0 2   x tgxlim 0 2   x Анықтама: Егер f(x) функциясының нүктесіндегі бір жақты шегі , болса, яғни немесе болса, Онда түзуі f(x) функциясының вертикаль асимптотасы д.а. ax 0x )(limxf 0ax )(limxf 0ax ВертикальВертикаль ( ) тік ( ) тік асимптотаасимптота

3 слайд

2  2     2 3 2 3  x y 0 tgxy функциясы Вертикаль ( ) тік асимптотасыбар 2 3 ; 2 3 ; 2 ; 2   xxxx Znnx  , 2   Жалпытеңдеуі түзуі tgxlim 0 2   x tgxlim 0 2   x Анықтама: Егер f(x) функциясының нүктесіндегі бір жақты шегі , болса, яғни немесе болса, Онда түзуі f(x) функциясының вертикаль асимптотасы д.а. ax 0x )(limxf 0ax )(limxf 0ax ВертикальВертикаль ( ) тік ( ) тік асимптотаасимптота

4 слайд
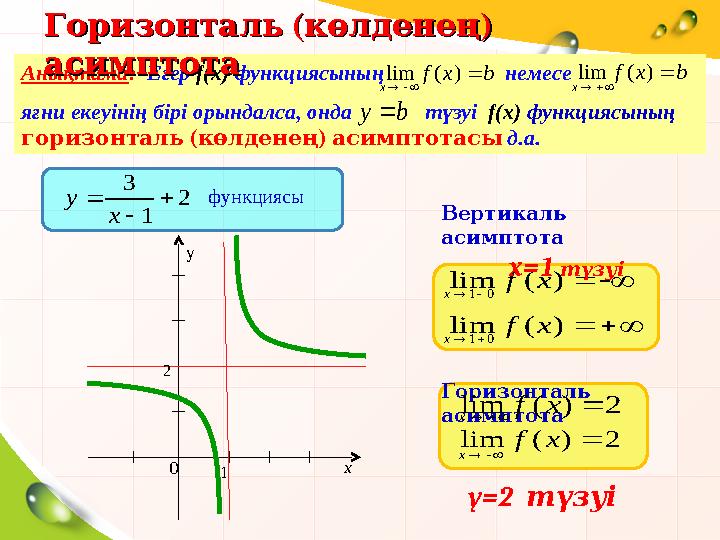
)(limxf 01x )(limxf 01x x y 0 2 1 3    x y функциясы 1 2 Вертикаль асимптота x=1 түзуі Горизонталь асимптота 2)(lim xf x 2)(lim xf x Анықтама: Егер f(x) функциясының немесе яғни екеуінің бірі орындалса, онда түзуі f(x) функциясының ( ) горизонталь көлденең асимптотасы д.а. by bxf)(lim x ГоризонтальГоризонталь ( ) көлденең ( ) көлденең асимптотаасимптота bxf)(lim x y=2 түзуі

4 слайд

)(limxf 01x )(limxf 01x x y 0 2 1 3    x y функциясы 1 2 Вертикаль асимптота x=1 түзуі Горизонталь асимптота 2)(lim xf x 2)(lim xf x Анықтама: Егер f(x) функциясының немесе яғни екеуінің бірі орындалса, онда түзуі f(x) функциясының ( ) горизонталь көлденең асимптотасы д.а. by bxf)(lim x ГоризонтальГоризонталь ( ) көлденең ( ) көлденең асимптотаасимптота bxf)(lim x y=2 түзуі

5 слайд
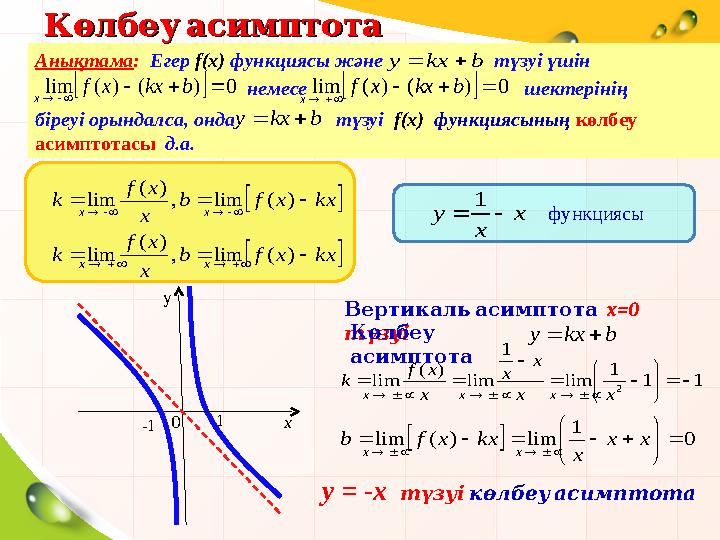
11 1 lim 1 lim )( lim 2          xx x x x xf k Вертикальасимптота x=0 түзуі    kxxfb x xf k kxxfb x xf k   )(lim, )( lim )(lim, )( lim x y 0 1 x Анықтама: Егер f(x) функциясы және түзуі үшін немесе шектерінің біреуі орындалса, онда түзуі f(x) функциясының көлбеу асимптотасы д.а. bkxy   0)()(lim  bkxxf x Көлбеуасимптота Көлбеуасимптота bkxy   0)()(lim  bkxxf x -1 x x x x bkxy  x   0 1 lim)(lim        xx x kxxfb x x y = -x түзуі көлбеуасимптота x x y 1 функциясы Көлбеу асимптота x

5 слайд

11 1 lim 1 lim )( lim 2          xx x x x xf k Вертикальасимптота x=0 түзуі    kxxfb x xf k kxxfb x xf k   )(lim, )( lim )(lim, )( lim x y 0 1 x Анықтама: Егер f(x) функциясы және түзуі үшін немесе шектерінің біреуі орындалса, онда түзуі f(x) функциясының көлбеу асимптотасы д.а. bkxy   0)()(lim  bkxxf x Көлбеуасимптота Көлбеуасимптота bkxy   0)()(lim  bkxxf x -1 x x x x bkxy  x   0 1 lim)(lim        xx x kxxfb x x y = -x түзуі көлбеуасимптота x x y 1 функциясы Көлбеу асимптота x