Материалдар / Презентация. Иррационал теңдеулер. 11-сынып

Презентация. Иррационал теңдеулер. 11-сынып

Материал туралы қысқаша түсінік

Материал мұғалімдерге көмегі бола ма деген оймен жіберіп отырмын

Канапиянова Майра Турдыбековна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

20 Сәуір 2019

1207

3 рет жүктелген

Алгебра Презентация 11 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 12

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд
• Иррационал теңдеудің анықтамасын және ирррациолнал теңдеулерді шешу әдістерін меңгерту; • Теңдеудің екі жақ бөлігің бірдей дәрежеге шығару және жаңа айнымалыны енгізу әдістерін есеп шығаруда пайдалану дағдыларын қалыптастыру;

2 слайд

• Иррационал теңдеудің анықтамасын және ирррациолнал теңдеулерді шешу әдістерін меңгерту; • Теңдеудің екі жақ бөлігің бірдей дәрежеге шығару және жаңа айнымалыны енгізу әдістерін есеп шығаруда пайдалану дағдыларын қалыптастыру;

3 слайд
Анықтама. Иррационал теңдеулер- деп белгісіз айнымалы х түбір таңбасының ішінде болатын теңдеулерді айтады.

3 слайд

Анықтама. Иррационал теңдеулер- деп белгісіз айнымалы х түбір таңбасының ішінде болатын теңдеулерді айтады.

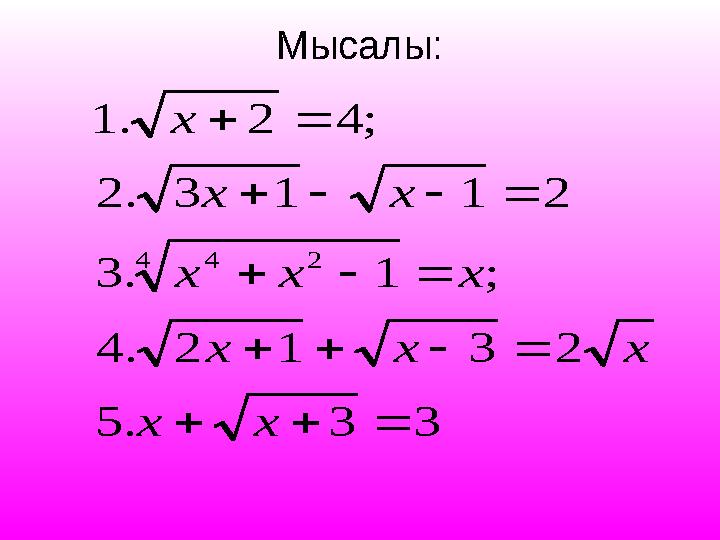
4 слайд
Мысалы:3 3 . 5 2 3 1 2 . 4 ; 1 . 3 2 1 1 3 . 2 ; 4 2 . 1 4 2 4                 x x x x x x x x x x x

4 слайд

Мысалы:3 3 . 5 2 3 1 2 . 4 ; 1 . 3 2 1 1 3 . 2 ; 4 2 . 1 4 2 4                 x x x x x x x x x x x

5 слайд
Иррационал теңдеулерді шешудің екі тәсілі бар: 1. теңдеудің екі жақ бөлігін бірдей дәрежеге шығару; 2. жаңа айнымалыны енгізу;

5 слайд

Иррационал теңдеулерді шешудің екі тәсілі бар: 1. теңдеудің екі жақ бөлігін бірдей дәрежеге шығару; 2. жаңа айнымалыны енгізу;

6 слайд
Теңдеудің екі жағын бірдей дәрежеге шығару тәсілі арқылы иррационал теңдеулерді шешу үшін келесі алгоритмді қолданамыз: 1) Берілген иррационал теңдеуді түрлендіру арқылы келесі түрге келтіреміз: ; 2) Теңдеудің екі жақ бөлігін n -ші дәрежеге шығарып , шешу әдісі белгілі f(x)=g(x) теңдеуін аламыз; 3) Соңғы теңдеуді шешіп, табылған түбірлерді берілген теңдеуге қойып тексереміз. 4) Теңдеуді қанағаттандыратын түбірлерді теңдеу түбірлері деп атаймыз. Қанағаттандырмайтын түбірлер теңдеудің “ бөгде түбірлері ” деп атайды.n n x g x f ) ( ) (  n n n n x g x f )) ( ( )) ( ( 

6 слайд

Теңдеудің екі жағын бірдей дәрежеге шығару тәсілі арқылы иррационал теңдеулерді шешу үшін келесі алгоритмді қолданамыз: 1) Берілген иррационал теңдеуді түрлендіру арқылы келесі түрге келтіреміз: ; 2) Теңдеудің екі жақ бөлігін n -ші дәрежеге шығарып , шешу әдісі белгілі f(x)=g(x) теңдеуін аламыз; 3) Соңғы теңдеуді шешіп, табылған түбірлерді берілген теңдеуге қойып тексереміз. 4) Теңдеуді қанағаттандыратын түбірлерді теңдеу түбірлері деп атаймыз. Қанағаттандырмайтын түбірлер теңдеудің “ бөгде түбірлері ” деп атайды.n n x g x f ) ( ) (  n n n n x g x f )) ( ( )) ( ( 

7 слайд
Кейде иррационал теңдеуді шешуді теңдеудің анықталу облысын, басқаша айтсақ, айнымалының мүмкін мәндер жиынын табудан бастаған ыңғайлы. Осыдан кейін табылған шешімдердің айнымалының мүмкін мәндер жиынына тиісті болатынын тексерсек жеткілікті. Айнымалының мүмкін мәндер жиынына тиісті емес шешімдер “бөгде” түбірлер болады.

7 слайд

Кейде иррационал теңдеуді шешуді теңдеудің анықталу облысын, басқаша айтсақ, айнымалының мүмкін мәндер жиынын табудан бастаған ыңғайлы. Осыдан кейін табылған шешімдердің айнымалының мүмкін мәндер жиынына тиісті болатынын тексерсек жеткілікті. Айнымалының мүмкін мәндер жиынына тиісті емес шешімдер “бөгде” түбірлер болады.

8 слайд
мысалы:                         . 0 , 3 , 2 1 0 , 0 3 , 0 1 2 2 3 1 2 x x x немесе x x x x x x 2 1  3 0 x x x    ; 3     7 4 4 0 16 24 7 , 4 4 12 24 4 8 , 4 4 ) 3 )(1 2( 4 , 2 3 1 2 2 , 4 3 3 1 2 2 1 2 , 2 3 1 2 2 3 1 2 2 1 2 2 2 2 2 2                                      x x x x x x x x x x x x x x x x x x x x x x x x x x x

8 слайд

мысалы:                         . 0 , 3 , 2 1 0 , 0 3 , 0 1 2 2 3 1 2 x x x немесе x x x x x x 2 1  3 0 x x x    ; 3     7 4 4 0 16 24 7 , 4 4 12 24 4 8 , 4 4 ) 3 )(1 2( 4 , 2 3 1 2 2 , 4 3 3 1 2 2 1 2 , 2 3 1 2 2 3 1 2 2 1 2 2 2 2 2 2                                      x x x x x x x x x x x x x x x x x x x x x x x x x x x

9 слайд
Кітаппен жұмыс • № 96, №97 есептерді шығару

9 слайд

Кітаппен жұмыс • № 96, №97 есептерді шығару

10 слайд
Actibvote- тест құрылғысының көмегімен 5 минуттық тест есептерін шығару

10 слайд

Actibvote- тест құрылғысының көмегімен 5 минуттық тест есептерін шығару

11 слайд