Презентация к научному проекту "Золотое сечение"

#1 слайд
ГУ « Общеобразовательная Сарыобинская средняя школа»      Проект на тему: «Золотое сечение»     Секция : математика     Автор проекта: Сериков Адиль, Терликбай Азамат . 6 «Б» класс Акмолинская область, Аршалынский район Сарыобинская средняя школа Руководитель проекта: Шишкина Галина Степановна Учитель математики Сарыобинская средняя школа     2019 – 2020 учебный год

1 слайд

#2 слайд
Проект на тему: «Золотое сечение»  Цель работы: доказать, что «золотое сечение» – верх совершенства и гармонии в природе. Элементы «золотого сечения» являются составляющей частью произведений известных художников Казахстана.   Задачи: Подобрать литературу по теме. Изучить понятие «золотое сечение»; Рассмотреть применение «золотого сечения » в архитектуре, искусстве, биологии; Исследовать присутствие золотого сечения в произведениях известных художников и скульпторов Казахстана.

2 слайд

#3 слайд
 Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему  А С В АС: АВ =СВ: АС  Мы решили изучить это понятие , познакомиться с применением «золотого сечения» в окружающем мире и исследовать присутствие золотого сечения в изобразительном искусстве и скульптуре известных Казахстанских художников и скульпторов

3 слайд

#4 слайд
Числа Фибоначчи С золотой пропорцией тесно связан ряд чисел Фибоначчи 1,1,2,3,5,8,13,21,34,55,89 и т.д. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления стремится к числу : Чем дальше мы будем продвигаться от начала ряда, тем лучше будет приближение. Если взять калькулятор и разделить каждое из них на предыдущее, то получиться: 1:1=1; 2:1=2; 3:2=1,5; 5:3=1,666666; 8:5=1,6; 13:8=1,625; 21:13=1,615384;… Для практических целей ограничиваются приблизительным значением Φ 1,618 или Φ 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 38 % к 62 % или 5 к 8.            

4 слайд

#5 слайд
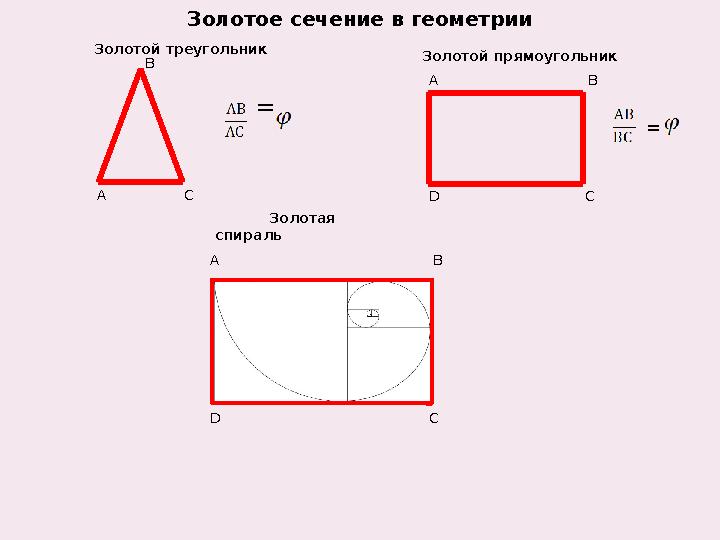
Золотое сечение в геометрии С В А Золотой треугольник Золотой прямоугольник А В D С Золотая спираль А В D С = =

5 слайд

#6 слайд
Примеры золотого сечения в окружающем мире Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение». Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках,

6 слайд

#7 слайд
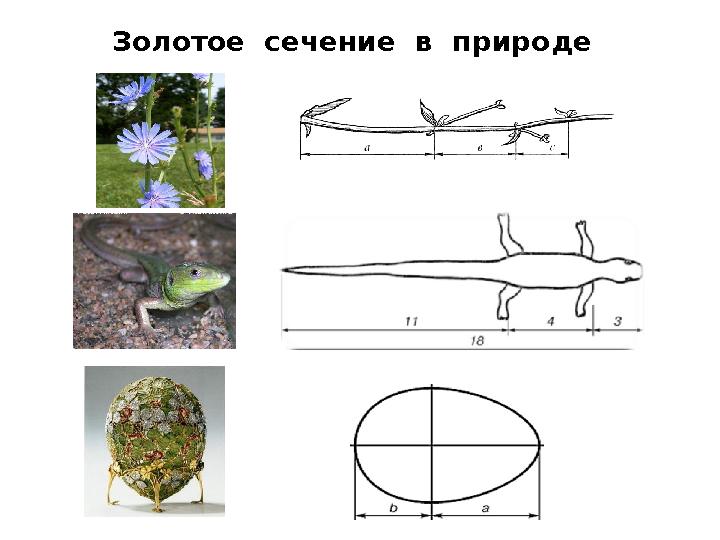
Золотое сечение в природе

7 слайд

#8 слайд

8 слайд

#9 слайд
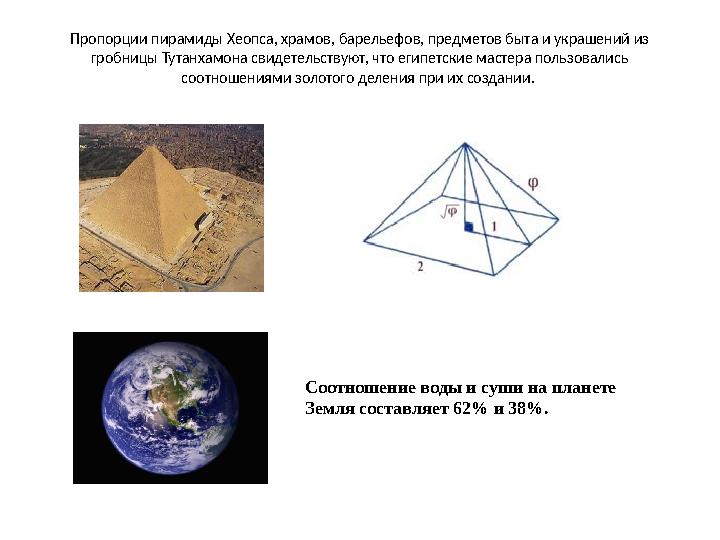
Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Соотношение воды и суши на планете Земля составляет 62% и 38%.

9 слайд

#10 слайд
Исследование. Присутствие золотого сечения в произведениях известных художников и скульпторов Казахстана. •Исследование присутствия золотого сечения в картинах Хлудова Николай Гавриловича- живописца, педагога, сыгравшего важную роль в подготовке первых казахских художников , чьи полотна посвящены жизни казахского народа  

10 слайд

#11 слайд
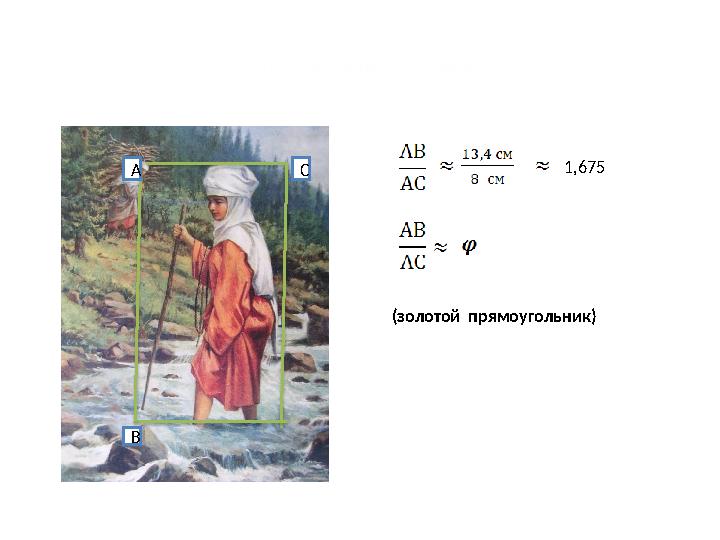
золотой прямоугольник 1,675 (золотой прямоугольник) А С В

11 слайд

#12 слайд
Золотая спираль

12 слайд

#13 слайд
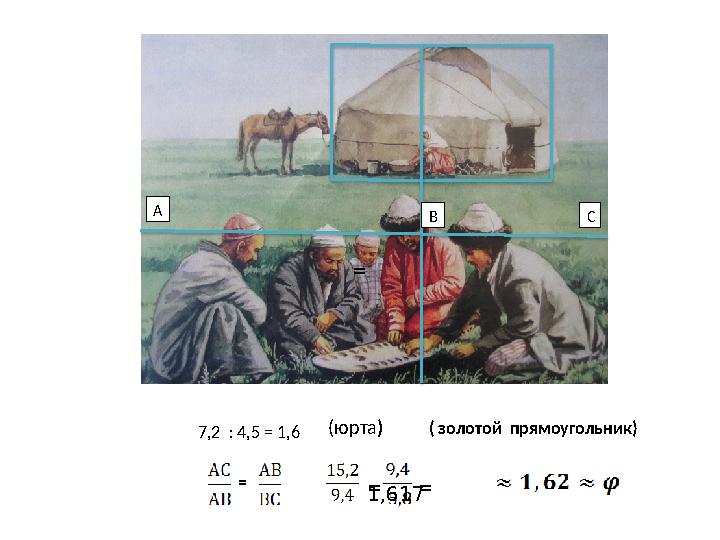
7,2 : 4,5 = 1,6 (юрта) ( золотой прямоугольник) А В С = = 1,617 ==

13 слайд

#14 слайд
А.Петров. «Встреча» А Д Е СВ = = 1,611,62 1,62 1,61 = = = (золотое сечение)

14 слайд

#15 слайд
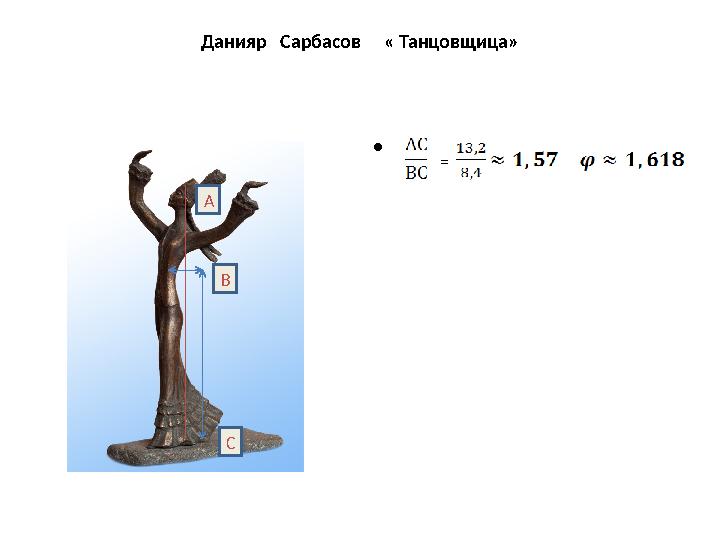
Данияр Сарбасов « Танцовщица» • А В С =

15 слайд

#16 слайд
•Исследование присутствия золотого сечения в картинах Абильхана Кастеева — казахского живописца и акварелиста, народного художника, основоположника казахского изобразительного искусства.

16 слайд

#17 слайд
  Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, они делят величину изображения по горизонтали и вертикали в золотом сечении, т.е. расположены они на расстоянии примерно 3/8 и 5/8 от соответствующих краев плоскости.   « Турксиб» ( 1969 г.) 11,2 : 6,9 6,9 : 4,3 15,2 : 9,4 9,4 : 5,8 9,4 : 5,8

17 слайд

#18 слайд
«Аксайский карьер» (1967 г.)

18 слайд

#19 слайд
Заключение  В ходе проделанной работы мы приходим к следующим выводам:  Цель достигнута:  1) Мы изучили понятие «Золотое сечение»  2) Доказали, что «золотое сечение» – верх совершенства и гармонии в природе.  3)Элементы «золотого сечения» являются составляющей частью произведений известных художников Казахстана.  Мы порой не осознаем, насколько наша жизнь связана с математикой. Даже такие творческие направления деятельности человека, как музыка, живопись, архитектура без математических законов не могут существовать и развиваться.  В своей работе мы постарались это показать , и считаем, что наша работа дает более широкие представления о математике и ее присутствии в окружающем нас мире. Представленные нами материалы будут интересны многим учащимся и покажут математику с новой стороны, с которой они ее еще ни разу не видели.  Кроме того наша работа поможет познакомиться с замечательными художниками , посвятившие свои произведения искусства нашей прекрасной казахстанской земле -нашей Родине . Красота и неповторимость этих картин обусловлена присутствием элементов «Золотого сечения», как одно из непременных условий совершенства и гармонии.  

19 слайд