Материалдар / Презентация "Квадрат теңсіздік. Квадрат теңсіздіктерді квадраттық функцияның графигі арқылы шығару" 8 сынып
Презентация "Квадрат теңсіздік. Квадрат теңсіздіктерді квадраттық функцияның графигі арқылы шығару" 8 сынып
Материал туралы қысқаша түсінік
Презентация "Квадрат теңсіздік. Квадрат теңсіздіктерді квадраттық функцияның графигі арқылы шығару" тақырыбна берілген, әріптестеріме көмегі тиеді деген ойдамын
Авторы:
28 Маусым 2018
5357
80 рет жүктелген
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 26
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
«Білімге жетелейтін үш жол бар:
Еліктеу жолы - ең жеңіл жол,
Ойлау жолы - ең игілікті жол,
Тәжірибе жолы - ең қиын да, ащы жол».
Конфуций.
1 слайд
«Білімге жетелейтін үш жол бар: Еліктеу жолы - ең жеңіл жол, Ойлау жолы - ең игілікті жол, Тәжірибе жолы - ең қиын да, ащы жол». Конфуций.
2 слайд
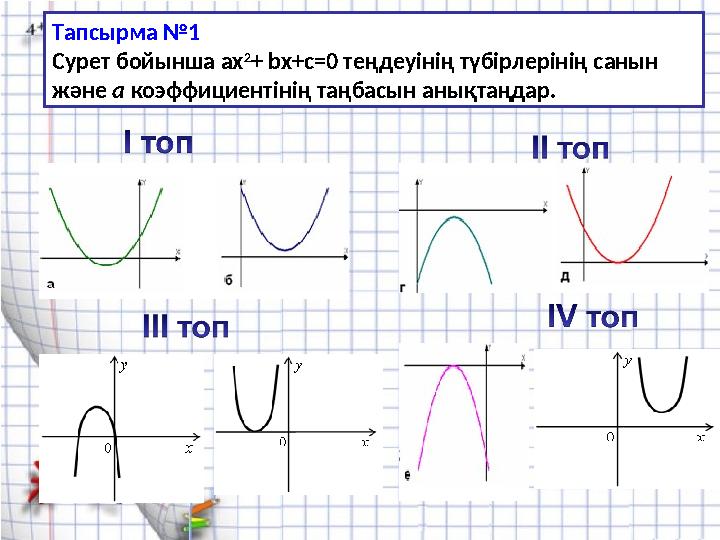
Тапсырма №1
Сурет бойынша ax
2
+ bx+c=0 теңдеуінің түбірлерінің санын
және а коэффициентінің таңбасын анықтаңдар.
2 слайд
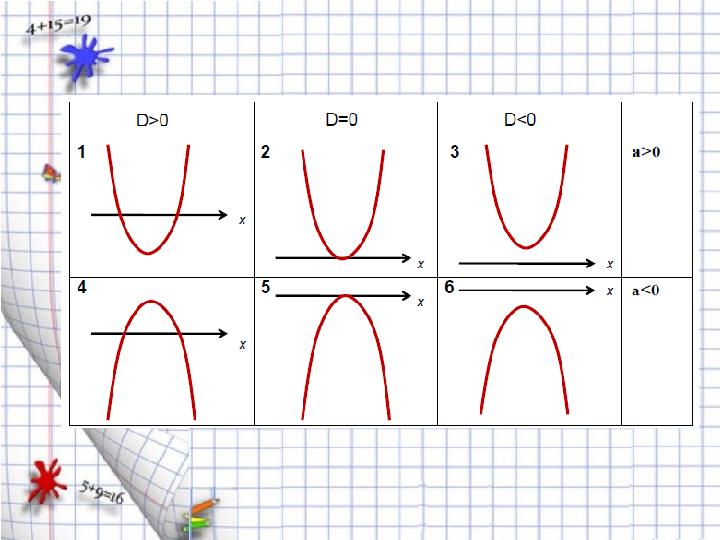
Тапсырма №1 Сурет бойынша ax 2 + bx+c=0 теңдеуінің түбірлерінің санын және а коэффициентінің таңбасын анықтаңдар.
3 слайд
3 слайд
4 слайд
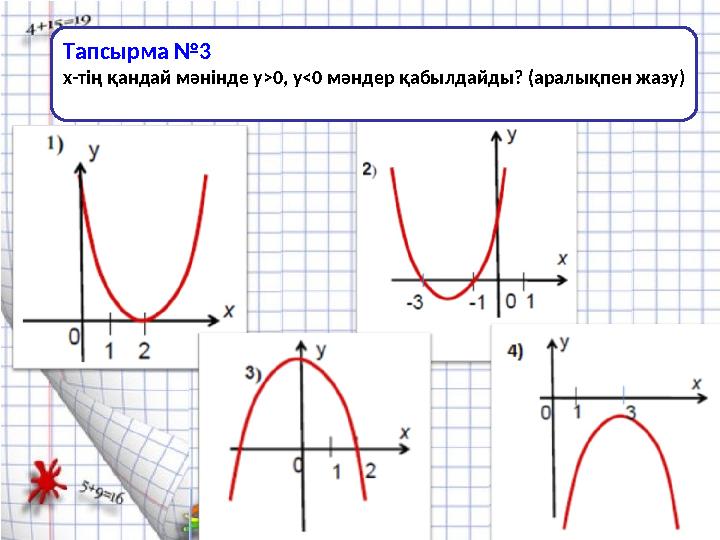
Тапсырма №3
х-тің қандай мәнінде у>0, у<0 мәндер қабылдайды? (аралықпен жазу)
4 слайд
Тапсырма №3 х-тің қандай мәнінде у>0, у<0 мәндер қабылдайды? (аралықпен жазу)
5 слайд
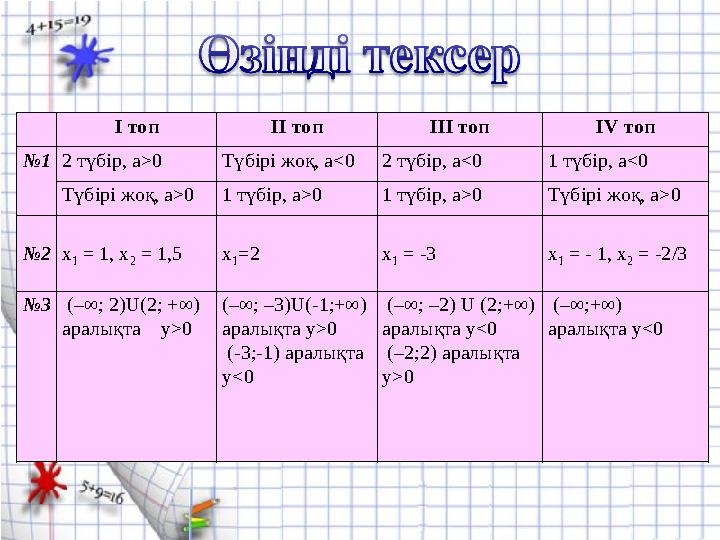
І топ ІІ топ ІІІ топ ІV топ
№12 түбір, а>0 Түбірі жоқ, а<02 түбір, а<0 1 түбір, а<0
Түбірі жоқ, а>01 түбір, а>0 1 түбір, а>0 Түбірі жоқ, а>0
№2х
1
= 1, x
2
= 1,5 х
1
=2 х
1
= -3 х
1
= - 1, x
2
= -2/3
№3 (–∞; 2)U(2; +∞)
аралықта у>0
(–∞; –3)U(-1;+∞)
аралықта у>0
(-3;-1) аралықта
у<0
(–∞; –2) U (2;+∞)
аралықта у<0
(–2;2) аралықта
у>0
(–∞;+∞)
аралықта у<0
5 слайд
І топ ІІ топ ІІІ топ ІV топ №12 түбір, а>0 Түбірі жоқ, а<02 түбір, а<0 1 түбір, а<0 Түбірі жоқ, а>01 түбір, а>0 1 түбір, а>0 Түбірі жоқ, а>0 №2х 1 = 1, x 2 = 1,5 х 1 =2 х 1 = -3 х 1 = - 1, x 2 = -2/3 №3 (–∞; 2)U(2; +∞) аралықта у>0 (–∞; –3)U(-1;+∞) аралықта у>0 (-3;-1) аралықта у<0 (–∞; –2) U (2;+∞) аралықта у<0 (–2;2) аралықта у>0 (–∞;+∞) аралықта у<0
6 слайд
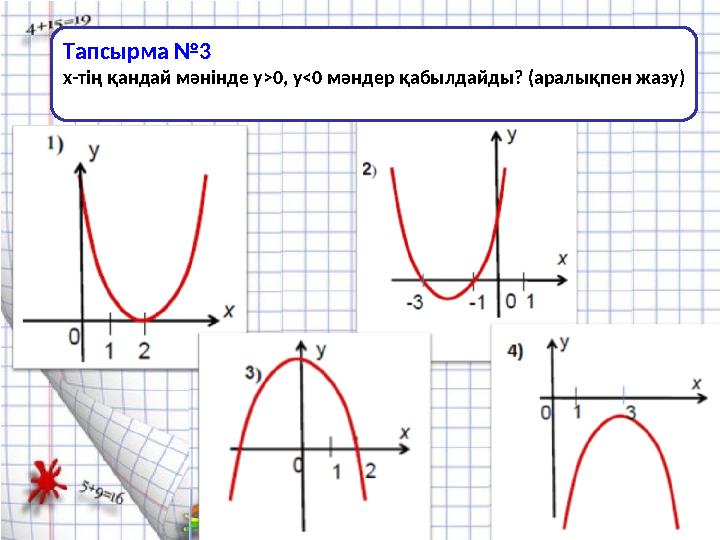
Тапсырма №3
х-тің қандай мәнінде у>0, у<0 мәндер қабылдайды? (аралықпен жазу)
6 слайд
Тапсырма №3 х-тің қандай мәнінде у>0, у<0 мәндер қабылдайды? (аралықпен жазу)
7 слайд
14.03.2018
7 слайд
14.03.2018
8 слайд
Қандай теңсіздіктерді бір
айнымалысы бар квадрат теңсіздіктер
дейміз?Анықтама:
aх
2
+ bх +с >0 , aх
2
+ bх +с <0 , aх
2
+ bх +с ≥0 , aх
2
+ +bх+ с ≤ 0 түріндегі теңсіздіктер квадрат
теңсіздіктер деп аталады.
Анықтама:
aх
2
+ bх +с >0 , aх
2
+ bх +с <0 , aх
2
+ bх +с ≥0 , aх
2
+ +bх+ с ≤ 0 түріндегі теңсіздіктер квадрат
теңсіздіктер деп аталады.
8 слайд
Қандай теңсіздіктерді бір айнымалысы бар квадрат теңсіздіктер дейміз?Анықтама: aх 2 + bх +с >0 , aх 2 + bх +с <0 , aх 2 + bх +с ≥0 , aх 2 + +bх+ с ≤ 0 түріндегі теңсіздіктер квадрат теңсіздіктер деп аталады. Анықтама: aх 2 + bх +с >0 , aх 2 + bх +с <0 , aх 2 + bх +с ≥0 , aх 2 + +bх+ с ≤ 0 түріндегі теңсіздіктер квадрат теңсіздіктер деп аталады.
9 слайд
1) 2х – 6 < 0 2) (2+ х)(х – 6) > 0 3) 2х – 6 – х
3
≥ 0 4) х
2
+ 2х – 3 = 0
6) х(х + 2)(х – 3) < 0
7) х
2
+ ≤ 6х+5
5) х
2
+ 2х – 3 ≥ 0
ИӘ ЖОҚ
9 слайд
1) 2х – 6 < 0 2) (2+ х)(х – 6) > 0 3) 2х – 6 – х 3 ≥ 0 4) х 2 + 2х – 3 = 0 6) х(х + 2)(х – 3) < 0 7) х 2 + ≤ 6х+5 5) х 2 + 2х – 3 ≥ 0 ИӘ ЖОҚ
10 слайд
10 слайд
11 слайд
11 слайд
12 слайд
555
1) 5х
2
+ 9x – 2 = 0
2) а > 0 – тармақтары
жоғары бағытталған
3) х
1
= -2; Х
2
= 0,5
5х
2
+ 9x - 2 < 0
У
Х
0
1
0,5-2
-2 < х < 0,5
Жауабы: ( -2; 0,5 )
-
12 слайд
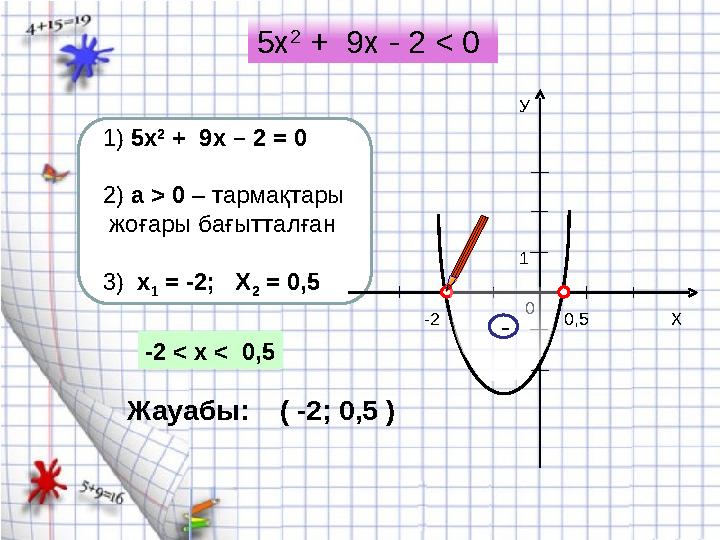
555 1) 5х 2 + 9x – 2 = 0 2) а > 0 – тармақтары жоғары бағытталған 3) х 1 = -2; Х 2 = 0,5 5х 2 + 9x - 2 < 0 У Х 0 1 0,5-2 -2 < х < 0,5 Жауабы: ( -2; 0,5 ) -
13 слайд
1. Теңсіздікті aх
2
+ bх +с >0 , aх
2
+ bх +с <0 түрге
келтіру;
2. y=ax
2
+bx+c функцияны қарастыру;
3. Тармақтарының бағытын анықтау;
4. Абсцисса осімен қиылысу нүктелерін табу (y=0,
ax
2
+bx+c=0 теңдеуінің түбірлерні табу);
5. y=ax
2
+bx+c функция графигін схемалық түрде
салу;
6. Абсцисса осінде у>0, у<0 аралықтарын сызып
көрсету;
7. Жауабын аралық түрде жазу.
Квадрат теңсіздіктерді шешу алгоритмі:
13 слайд
1. Теңсіздікті aх 2 + bх +с >0 , aх 2 + bх +с <0 түрге келтіру; 2. y=ax 2 +bx+c функцияны қарастыру; 3. Тармақтарының бағытын анықтау; 4. Абсцисса осімен қиылысу нүктелерін табу (y=0, ax 2 +bx+c=0 теңдеуінің түбірлерні табу); 5. y=ax 2 +bx+c функция графигін схемалық түрде салу; 6. Абсцисса осінде у>0, у<0 аралықтарын сызып көрсету; 7. Жауабын аралық түрде жазу. Квадрат теңсіздіктерді шешу алгоритмі:
14 слайд
14 слайд
15 слайд
І топ - №284 (1),
ІІ топ - №284(2),
ІІІ топ №284 (3),
ІV топ - №284(4)
15 слайд
І топ - №284 (1), ІІ топ - №284(2), ІІІ топ №284 (3), ІV топ - №284(4)
16 слайд
16 слайд
17 слайд
.065
2
xx
.065
2
xx
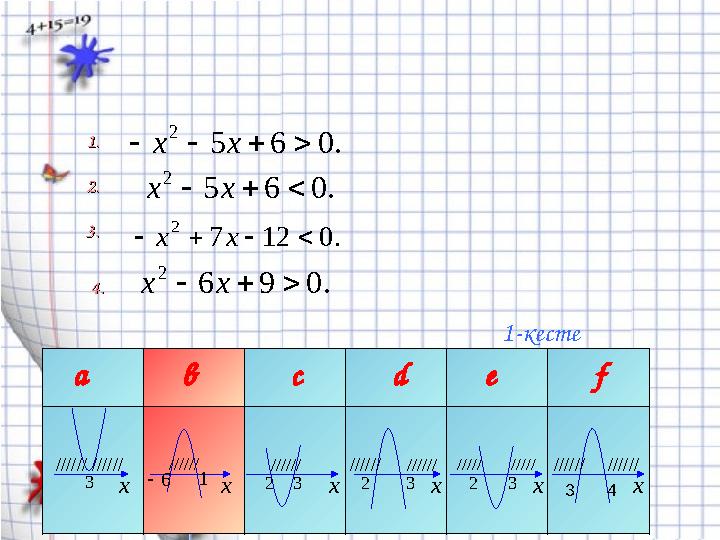
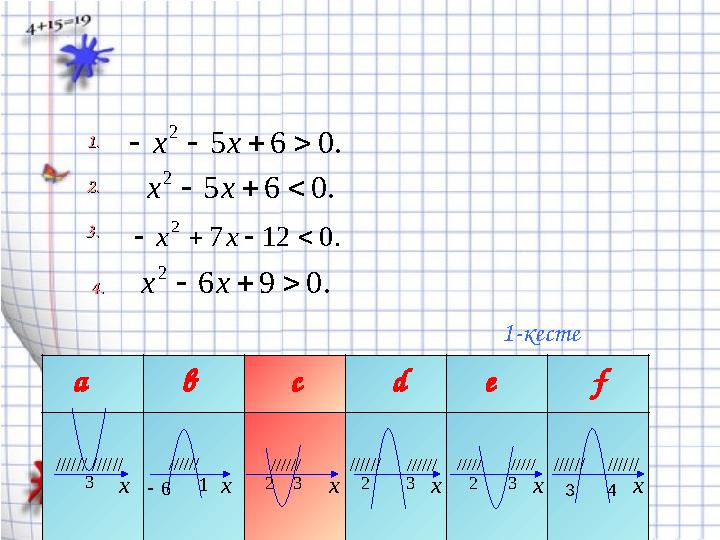
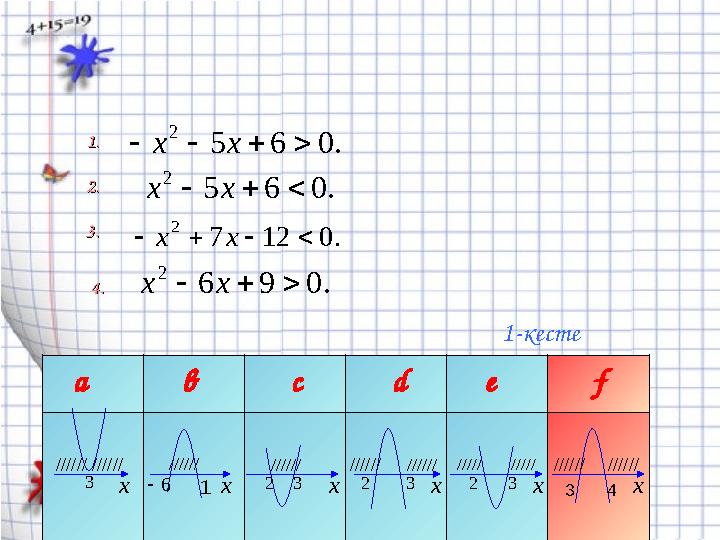
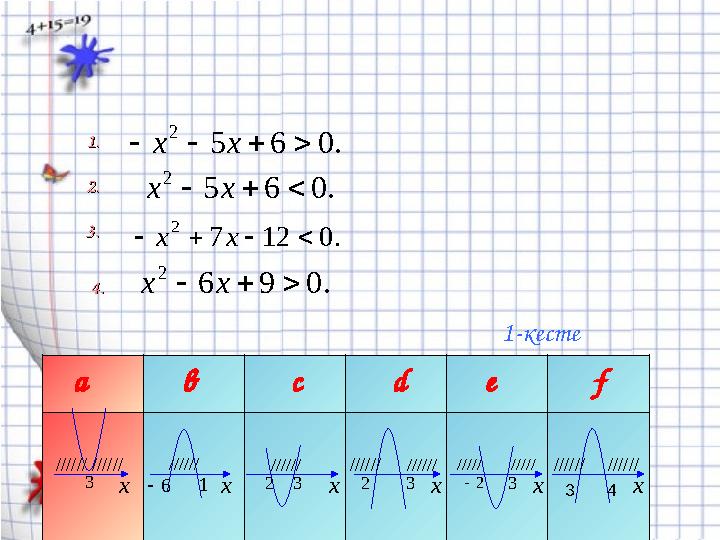
1-кестеден әр теңсіздіктің шешімін табыңдар:1-кестеден әр теңсіздіктің шешімін табыңдар:
1.1.
2.2.
3.3.
4.4.
а в с d e f
x x x x x x6 2 2 23 1 33 3
////// ////// /////////// //////
1-кесте
.0127
2
xx
.096
2
xx
43
////////////////////////
/////
17 слайд
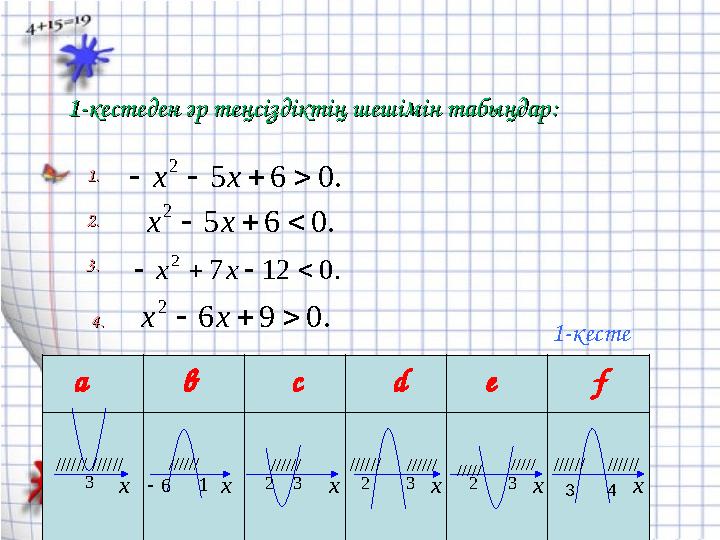
.065 2 xx .065 2 xx 1-кестеден әр теңсіздіктің шешімін табыңдар:1-кестеден әр теңсіздіктің шешімін табыңдар: 1.1. 2.2. 3.3. 4.4. а в с d e f x x x x x x6 2 2 23 1 33 3 ////// ////// /////////// ////// 1-кесте .0127 2 xx .096 2 xx 43 //////////////////////// /////
18 слайд
а в с d e f
x x x x x x
6 2 2 23 1 33 3
////// ////// /////////// //////
1-кесте
43
//////////////////////// /////
.065
2
xx
.065
2
xx
1.1.
2.2.
3.3.
4.4.
.0127
2
xx
.096
2
xx
18 слайд
а в с d e f x x x x x x 6 2 2 23 1 33 3 ////// ////// /////////// ////// 1-кесте 43 //////////////////////// ///// .065 2 xx .065 2 xx 1.1. 2.2. 3.3. 4.4. .0127 2 xx .096 2 xx
19 слайд
а в с d e f
x x x x x x6
2 2 23 1 33 3
////// ////// /////////// //////
1-кесте
43
//////////////////////// /////
.065
2
xx
.065
2
xx
1.1.
2.2.
3.3.
4.4.
.0127
2
xx
.096
2
xx
19 слайд
а в с d e f x x x x x x6 2 2 23 1 33 3 ////// ////// /////////// ////// 1-кесте 43 //////////////////////// ///// .065 2 xx .065 2 xx 1.1. 2.2. 3.3. 4.4. .0127 2 xx .096 2 xx
20 слайд
а в с d e f
x x x x x x6 2 2 23
1
33 3
////// ////// /////////// //////
1-кесте
43
//////////////////////// /////
.065
2
xx
.065
2
xx
1.1.
2.2.
3.3.
4.4.
.0127
2
xx
.096
2
xx
20 слайд
а в с d e f x x x x x x6 2 2 23 1 33 3 ////// ////// /////////// ////// 1-кесте 43 //////////////////////// ///// .065 2 xx .065 2 xx 1.1. 2.2. 3.3. 4.4. .0127 2 xx .096 2 xx
21 слайд
а в с d e f
x x x x x x6 2 2 23 1 33 3
////// ////// /////////// //////
1-кесте
43
//////////////////////// /////
.065
2
xx
.065
2
xx
1.1.
2.2.
3.3.
4.4.
.0127
2
xx
.096
2
xx
21 слайд
а в с d e f x x x x x x6 2 2 23 1 33 3 ////// ////// /////////// ////// 1-кесте 43 //////////////////////// ///// .065 2 xx .065 2 xx 1.1. 2.2. 3.3. 4.4. .0127 2 xx .096 2 xx
22 слайд
•§15 98-103 бет.§15 98-103 бет.
•№ № 282, 286 282, 286
•101 бет кестені толтыру 101 бет кестені толтыру
22 слайд
•§15 98-103 бет.§15 98-103 бет. •№ № 282, 286 282, 286 •101 бет кестені толтыру 101 бет кестені толтыру
23 слайд
Венн диаграммасы
•“Квадрат теңдеу” мен “квадрат теңсіздік”
ұғымдарының ұқсастығы мен
айырмашылығы
23 слайд
Венн диаграммасы •“Квадрат теңдеу” мен “квадрат теңсіздік” ұғымдарының ұқсастығы мен айырмашылығы
24 слайд
Тиісті тақырып астына өзіңіз білетіннің
барлығын жазыңыз:
“Квадрат теңдеу”
“Квадрат теңсіздік”
24 слайд
Тиісті тақырып астына өзіңіз білетіннің барлығын жазыңыз: “Квадрат теңдеу” “Квадрат теңсіздік”
25 слайд
Сөздің өзін пайдаланбастан бүгінгі сабақтың әрбір негізгі сөзін
түсіндіру үшін сізде бір минут бар:
квадрат
дискриминант
парабола
түбір
>, <
квадрат үшмүше
(а;b)
квадрат теңдеу
25 слайд
Сөздің өзін пайдаланбастан бүгінгі сабақтың әрбір негізгі сөзін түсіндіру үшін сізде бір минут бар: квадрат дискриминант парабола түбір >, < квадрат үшмүше (а;b) квадрат теңдеу
