Материалдар / Презентация "Логарифмдік теңдеулер және оларды шешу" 11 сынып

Презентация "Логарифмдік теңдеулер және оларды шешу" 11 сынып

Материал туралы қысқаша түсінік

Логарифмдік теңдеулер тақырыбы өте қызық және маңызды болып табылады. Сондықтан осы тақырыпты оқушыларға жете түсіндіру үшін түрлі әдіс-тәсілдерді сабақта пайдалану өте маңызды.Логарифмдік теңдеу туралы түсінік беріп, оның басқа теңдеулерден айырмашылығы мен ұқсастығын ұғындыру, логарифмдік теңдеулерді шешудің әдістерімен таныстырып, теңдеудің берілуіне байланысты әдісті дұрыс әрі тиімді пайдалану жолдарын көрсету мақсатында бірнеші тапсырмалардан құралған презентация құрастырған болатынмын. Өз тәжірибемде бұл презентация жақсы нәтиже бергендіктен, мұғалімдерге көмегі бола деген мақсатпен жариялап отырмын.

Тулешова Сабира Сабырбайқызы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

21 Желтоқсан 2017

2657

7 рет жүктелген

Алгебра Презентация 11 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 38

Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз!

Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі.

Оқу-ағарту министірлігінің ресми жауабы

Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!

Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз!

Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!

Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз!

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд

3 слайд
I.БәйгеБәйге

3 слайд

I.БәйгеБәйге

4 слайд
II.II. Есептер Есептер эстафетасы.эстафетасы.

4 слайд

II.II. Есептер Есептер эстафетасы.эстафетасы.

5 слайд
III. III. Формуланы Формуланы жалғастырыңызжалғастырыңыз ..

5 слайд

III. III. Формуланы Формуланы жалғастырыңызжалғастырыңыз ..

6 слайд
IV.IV. Ойлан тап. Ойлан тап.

6 слайд

IV.IV. Ойлан тап. Ойлан тап.

7 слайд
Логарифм дегеніміз не?Логарифм дегеніміз не?

7 слайд

Логарифм дегеніміз не?Логарифм дегеніміз не?

8 слайд
Шынайы логарифм мен Шынайы логарифм мен натурал логарифмнің натурал логарифмнің айырмашылығы?айырмашылығы?

8 слайд

Шынайы логарифм мен Шынайы логарифм мен натурал логарифмнің натурал логарифмнің айырмашылығы?айырмашылығы?

9 слайд
Көрсеткіштік функция Көрсеткіштік функция дегеніміз не?дегеніміз не?

9 слайд

Көрсеткіштік функция Көрсеткіштік функция дегеніміз не?дегеніміз не?

10 слайд
Теңдеу дегеніміз не?Теңдеу дегеніміз не?

10 слайд

Теңдеу дегеніміз не?Теңдеу дегеніміз не?

11 слайд
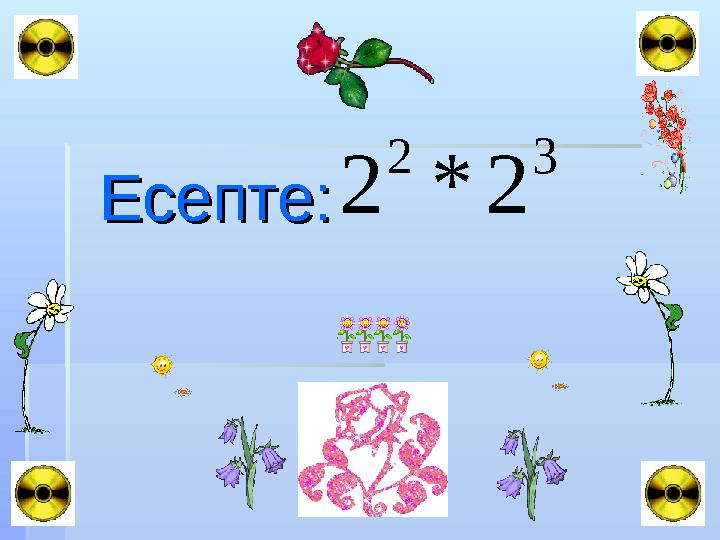
Есепте:Есепте: 32 2*2

11 слайд

Есепте:Есепте: 32 2*2

12 слайд
Логарифмдік функция деп Логарифмдік функция деп қай функцияны айтамыз?қай функцияны айтамыз?

12 слайд

Логарифмдік функция деп Логарифмдік функция деп қай функцияны айтамыз?қай функцияны айтамыз?

13 слайд
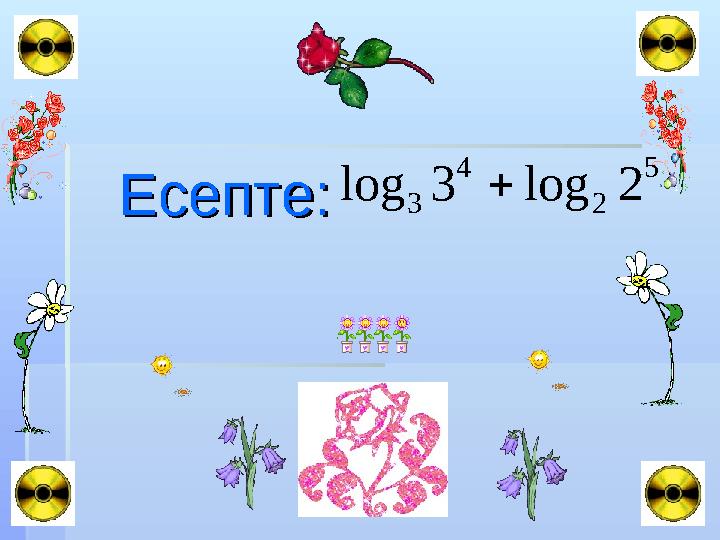
Есепте:Есепте: 5 2 4 3 2log3log

13 слайд

Есепте:Есепте: 5 2 4 3 2log3log

14 слайд
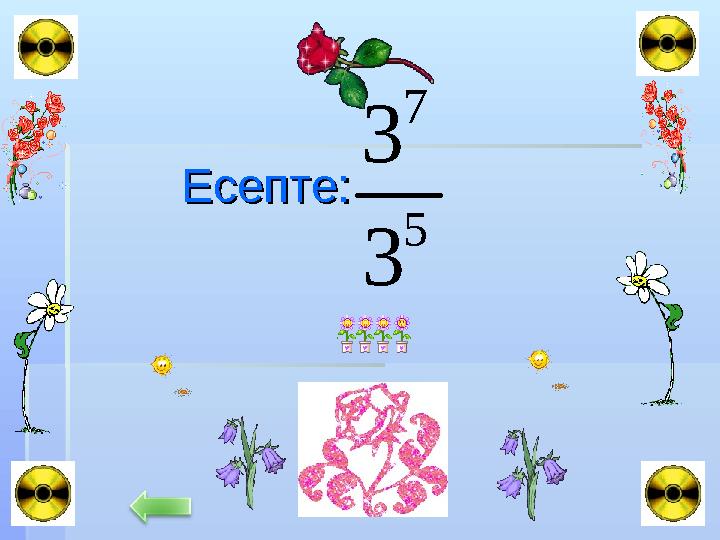
Есепте: Есепте: 5 7 3 3

14 слайд

Есепте: Есепте: 5 7 3 3

15 слайд
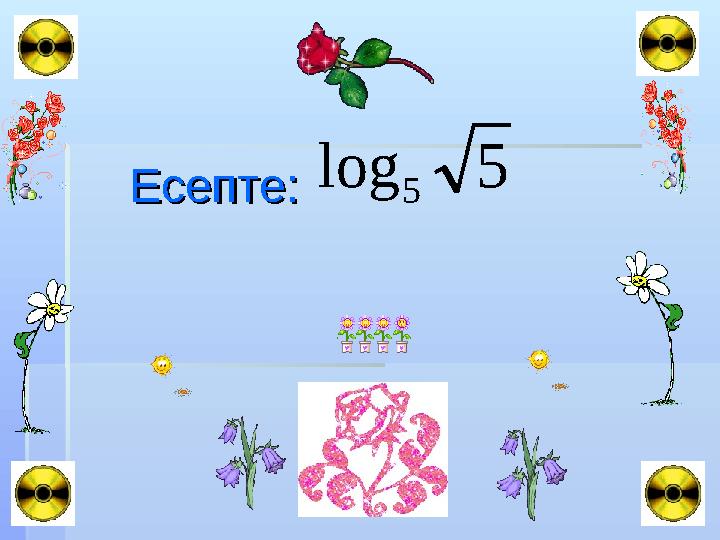
Есепте: Есепте: 5log 5

15 слайд

Есепте: Есепте: 5log 5

16 слайд
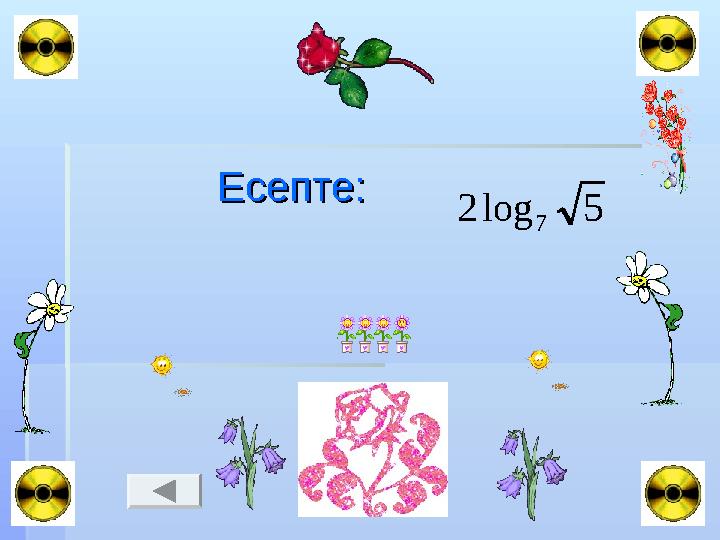
Есепте: Есепте: 5log2 7

16 слайд

Есепте: Есепте: 5log2 7

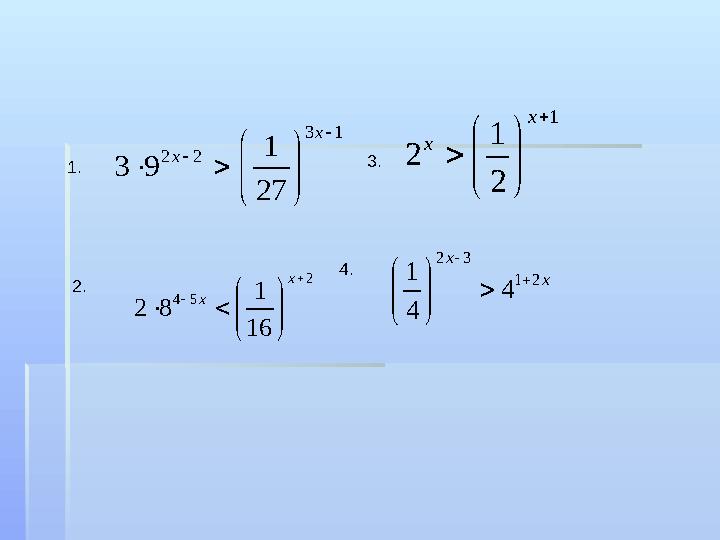
17 слайд
13 22 27 1 93          x x 1 2 1 2         x x x x 21 32 4 4 1        2 54 16 1 82          x x 1. 2. 3. 4.

17 слайд

13 22 27 1 93          x x 1 2 1 2         x x x x 21 32 4 4 1        2 54 16 1 82          x x 1. 2. 3. 4.

18 слайд
 13 6 613 14394 39441 33 333 3)3(3 27 1 93 39441 39441 13 3222 13 22                     x x xx xx xx xx x x x x

18 слайд

 13 6 613 14394 39441 33 333 3)3(3 27 1 93 39441 39441 13 3222 13 22                     x x xx xx xx xx x x x x

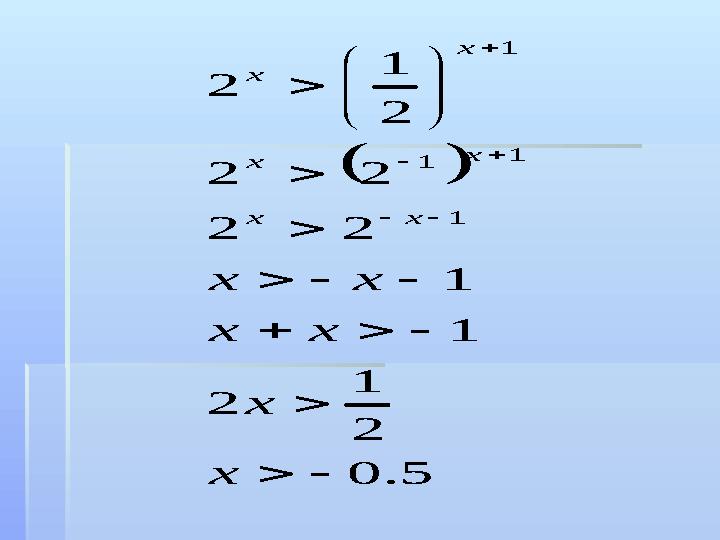
19 слайд
 5.0 2 1 2 1 1 22 22 2 1 2 1 1 1 1                  x x xx xx xx x x x x

19 слайд

 5.0 2 1 2 1 1 22 22 2 1 2 1 1 1 1                  x x xx xx xx x x x x

20 слайд
 10 1 2 11 21 2111 138415 8415121 22 2)2(2 16 1 82 8415121 2 4543 2 54                    x x x xx xx xx x x x x

20 слайд

 10 1 2 11 21 2111 138415 8415121 22 2)2(2 16 1 82 8415121 2 4543 2 54                    x x x xx xx xx x x x x

21 слайд
 5.0 4 2 24 3122 2132 44 44 4 4 1 2132 21 32 1 21 32                      x x x xx xx xx x x x x

21 слайд

 5.0 4 2 24 3122 2132 44 44 4 4 1 2132 21 32 1 21 32                      x x x xx xx xx x x x x

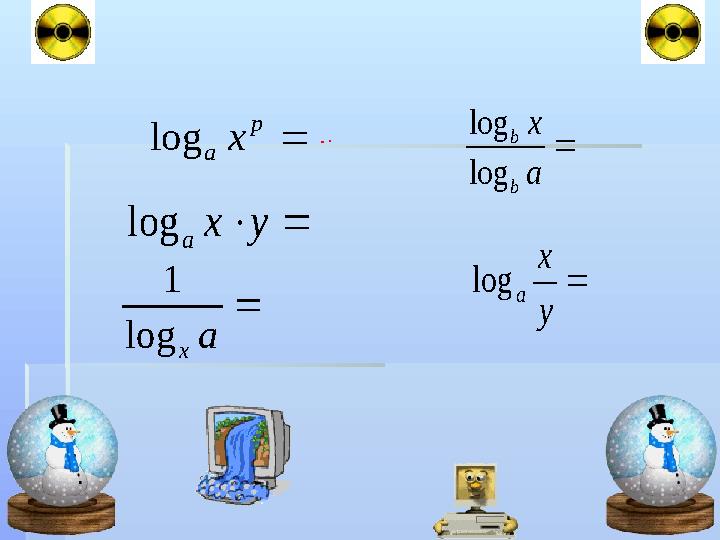
22 слайд
yx alog  y x alog  p axlog  a xlog 1  a x b b log log

22 слайд

yx alog  y x alog  p axlog  a xlog 1  a x b b log log

23 слайд
 b a a log  mn a  mn a  n cba)(  n a 1  0 a  mn a)(

23 слайд

 b a a log  mn a  mn a  n cba)(  n a 1  0 a  mn a)(

24 слайд
Бір топ торғай ұшып келіп ағаштың бұтағына қонады. Бір топ торғай ұшып келіп ағаштың бұтағына қонады. Бұтақ басына бір торғайдан қонса, бір торғай орынсыз Бұтақ басына бір торғайдан қонса, бір торғай орынсыз қалады. Ал бір бұтаққа екі торғайдан қонса, бір бұтақ артық. қалады. Ал бір бұтаққа екі торғайдан қонса, бір бұтақ артық. Сонда тороғай нешеу, бұтақ нешеу?Сонда тороғай нешеу, бұтақ нешеу?

24 слайд

Бір топ торғай ұшып келіп ағаштың бұтағына қонады. Бір топ торғай ұшып келіп ағаштың бұтағына қонады. Бұтақ басына бір торғайдан қонса, бір торғай орынсыз Бұтақ басына бір торғайдан қонса, бір торғай орынсыз қалады. Ал бір бұтаққа екі торғайдан қонса, бір бұтақ артық. қалады. Ал бір бұтаққа екі торғайдан қонса, бір бұтақ артық. Сонда тороғай нешеу, бұтақ нешеу?Сонда тороғай нешеу, бұтақ нешеу?

25 слайд
Баласы әкесіне - Әке маған жұмбақ Баласы әкесіне - Әке маған жұмбақ үйретші дейді. Сонда әкесі: - Сенің үйретші дейді. Сонда әкесі: - Сенің жасыңды үш есе көбейтсе менің жасыңды үш есе көбейтсе менің жасымдай болады. Ал менің жасымнан жасымдай болады. Ал менің жасымнан сенің жасыңды алып тастаса 20 қалады. сенің жасыңды алып тастаса 20 қалады. Мен нешедемін ? Сен нешедесің ?Мен нешедемін ? Сен нешедесің ?

25 слайд

Баласы әкесіне - Әке маған жұмбақ Баласы әкесіне - Әке маған жұмбақ үйретші дейді. Сонда әкесі: - Сенің үйретші дейді. Сонда әкесі: - Сенің жасыңды үш есе көбейтсе менің жасыңды үш есе көбейтсе менің жасымдай болады. Ал менің жасымнан жасымдай болады. Ал менің жасымнан сенің жасыңды алып тастаса 20 қалады. сенің жасыңды алып тастаса 20 қалады. Мен нешедемін ? Сен нешедесің ?Мен нешедемін ? Сен нешедесің ?

26 слайд
8 метр матадан ешқандай өлшеу құралысыз 5 метр мата 8 метр матадан ешқандай өлшеу құралысыз 5 метр мата қалай бөліп алуға болады?қалай бөліп алуға болады?

26 слайд

8 метр матадан ешқандай өлшеу құралысыз 5 метр мата 8 метр матадан ешқандай өлшеу құралысыз 5 метр мата қалай бөліп алуға болады?қалай бөліп алуға болады?

27 слайд
ЖоспарЖоспар 1. Логарифмдік теңдеу 1. Логарифмдік теңдеу анықтамасы.анықтамасы. 2. Логарифмдік теңдеуді шешу 2. Логарифмдік теңдеуді шешу әдістері.әдістері. 3.Логарифмдік теңдеулерді 3.Логарифмдік теңдеулерді шешуге мысалдар.шешуге мысалдар.

27 слайд

ЖоспарЖоспар 1. Логарифмдік теңдеу 1. Логарифмдік теңдеу анықтамасы.анықтамасы. 2. Логарифмдік теңдеуді шешу 2. Логарифмдік теңдеуді шешу әдістері.әдістері. 3.Логарифмдік теңдеулерді 3.Логарифмдік теңдеулерді шешуге мысалдар.шешуге мысалдар.

28 слайд
Логарифмдік теңдеулерді шешу Логарифмдік теңдеулерді шешу әдістері:әдістері: 1.1.Тікелей логарифмнің анықтамасы Тікелей логарифмнің анықтамасы бойынша шешу.бойынша шешу. 2.2.Потенциалдау әдісі.Потенциалдау әдісі. 3.3.Жаңа белгісіз енгізу әдісі.Жаңа белгісіз енгізу әдісі. 4.4.Мүшелеп логарифмдеу әдісі.Мүшелеп логарифмдеу әдісі.

28 слайд

Логарифмдік теңдеулерді шешу Логарифмдік теңдеулерді шешу әдістері:әдістері: 1.1.Тікелей логарифмнің анықтамасы Тікелей логарифмнің анықтамасы бойынша шешу.бойынша шешу. 2.2.Потенциалдау әдісі.Потенциалдау әдісі. 3.3.Жаңа белгісіз енгізу әдісі.Жаңа белгісіз енгізу әдісі. 4.4.Мүшелеп логарифмдеу әдісі.Мүшелеп логарифмдеу әдісі.

29 слайд
Белгісіз шамасы логарифмдік Белгісіз шамасы логарифмдік өрнектің ішінде болатын теңдеуді өрнектің ішінде болатын теңдеуді логарифмдіклогарифмдік теңдеу деп атаймыз теңдеу деп атаймыз

29 слайд

Белгісіз шамасы логарифмдік Белгісіз шамасы логарифмдік өрнектің ішінде болатын теңдеуді өрнектің ішінде болатын теңдеуді логарифмдіклогарифмдік теңдеу деп атаймыз теңдеу деп атаймыз

30 слайд
1.1.Тікелей логарифмнің Тікелей логарифмнің анықтамасы бойынша шешу.анықтамасы бойынша шешу. ca bc b a  log 3)34(log 2 2 xxМысал:

30 слайд

1.1.Тікелей логарифмнің Тікелей логарифмнің анықтамасы бойынша шешу.анықтамасы бойынша шешу. ca bc b a  log 3)34(log 2 2 xxМысал:

31 слайд
Белгісіз шамасы логарифмдік Белгісіз шамасы логарифмдік өрнектің ішінде болдатын теңдеуді өрнектің ішінде болдатын теңдеуді логарифмдіклогарифмдік теңдеу деп атаймыз теңдеу деп атаймыз

31 слайд

Белгісіз шамасы логарифмдік Белгісіз шамасы логарифмдік өрнектің ішінде болдатын теңдеуді өрнектің ішінде болдатын теңдеуді логарифмдіклогарифмдік теңдеу деп атаймыз теңдеу деп атаймыз

32 слайд
Логарифмдік теңдеуге мысалдар.Логарифмдік теңдеуге мысалдар.  4672log 3 x   230log202log 22 x 02loglog 3 2 3  xx

32 слайд

Логарифмдік теңдеуге мысалдар.Логарифмдік теңдеуге мысалдар.  4672log 3 x   230log202log 22 x 02loglog 3 2 3  xx

33 слайд
2. Потенциалдау әдісі.2. Потенциалдау әдісі. Потенциалдау дегеніміз - логарифмнің Потенциалдау дегеніміз - логарифмнің қасиеттерін пайдалану арқылы шешу.қасиеттерін пайдалану арқылы шешу. Мысал:Мысал: 3log2)21(log)4(log 222  xx

33 слайд

2. Потенциалдау әдісі.2. Потенциалдау әдісі. Потенциалдау дегеніміз - логарифмнің Потенциалдау дегеніміз - логарифмнің қасиеттерін пайдалану арқылы шешу.қасиеттерін пайдалану арқылы шешу. Мысал:Мысал: 3log2)21(log)4(log 222  xx

34 слайд
3. Жаңа белгісіз енгізу әдісі.3. Жаңа белгісіз енгізу әдісі. Есепті оңайлату мақсатында жаңа белгісіз Есепті оңайлату мақсатында жаңа белгісіз енгізіп квадрат теңдеуге келтіреміз.енгізіп квадрат теңдеуге келтіреміз. 03log7log2 3 2 3  xxМысал:

34 слайд

3. Жаңа белгісіз енгізу әдісі.3. Жаңа белгісіз енгізу әдісі. Есепті оңайлату мақсатында жаңа белгісіз Есепті оңайлату мақсатында жаңа белгісіз енгізіп квадрат теңдеуге келтіреміз.енгізіп квадрат теңдеуге келтіреміз. 03log7log2 3 2 3  xxМысал:

35 слайд
4. Мүшелеп логарифмдеу әдісі.4. Мүшелеп логарифмдеу әдісі. Берілген әрбір өрнекті мүшелеп Берілген әрбір өрнекті мүшелеп логарифмдеп қарапайым теңдеуге логарифмдеп қарапайым теңдеуге келтіреміз.келтіреміз. 125 2log 5  x x

35 слайд

4. Мүшелеп логарифмдеу әдісі.4. Мүшелеп логарифмдеу әдісі. Берілген әрбір өрнекті мүшелеп Берілген әрбір өрнекті мүшелеп логарифмдеп қарапайым теңдеуге логарифмдеп қарапайым теңдеуге келтіреміз.келтіреміз. 125 2log 5  x x

36 слайд
тт уу ғғ аа нн жж ее рр 1) 4672log 3 x 2)   230log202log 22 x 3) 02loglog 3 2 3  xx 4) Белгісіз шамасы логарифмдік өрнектің ішінде болатын теңдеу. 5) Негізі е санына тең болатын логарифм қалай аталады?    110log10log 33  xx 8 2log 2  x x7) 6)  34log 2 2 xx8)

36 слайд

тт уу ғғ аа нн жж ее рр 1) 4672log 3 x 2)   230log202log 22 x 3) 02loglog 3 2 3  xx 4) Белгісіз шамасы логарифмдік өрнектің ішінде болатын теңдеу. 5) Негізі е санына тең болатын логарифм қалай аталады?    110log10log 33  xx 8 2log 2  x x7) 6)  34log 2 2 xx8)

37 слайд
Үй тапсырмасы )54(log)1(log 55  xx )21(log)4(log 22 xx  2lg)1lg(lg xx 4lglg)5(lg  xx 3lg)1lg()1(lg  xx 10)3lg(lg xx 125 2log1)2(log 03log7log2 2log 6 2 6 3 2 3 5    x x xx x

37 слайд

Үй тапсырмасы )54(log)1(log 55  xx )21(log)4(log 22 xx  2lg)1lg(lg xx 4lglg)5(lg  xx 3lg)1lg()1(lg  xx 10)3lg(lg xx 125 2log1)2(log 03log7log2 2log 6 2 6 3 2 3 5    x x xx x