Презентация Тригонометриялық теңдеулерді және теңдеулер жүйесін шешу әдістері 10 сынып

1 слайд
Тригонометриялық теңдеулерді және теңдеулер жүйесін шешу әдістері

1 слайд

2 слайд
Ауызша есептеу Теңдеуді шешіңдер: А) 3 х – 5 = 7 Б) х 2 – 8 х + 15 = 0 В) 4 х 2 – 4 х + 1= 0 Г) х 4 – 5 х 2 + 4 = 0 Д) 3 х 2 – 12 = 0 Жауабы: 4 3; 5 0,5 -2; -1; 1; 2 -2; 2

2 слайд

3 слайд
Ауызша есептеу Өрнектерді ықшамдаңдар: А) (sin a – 1) (sin a + 1) Б) sin 2 a – 1 + cos 2 a В) sin 2 a + tg a ctg a + cos 2 a Г) Жауаптары: - cos 2 a 0 2  |1- tg х| xtgtgx 2 21 

3 слайд

4 слайд
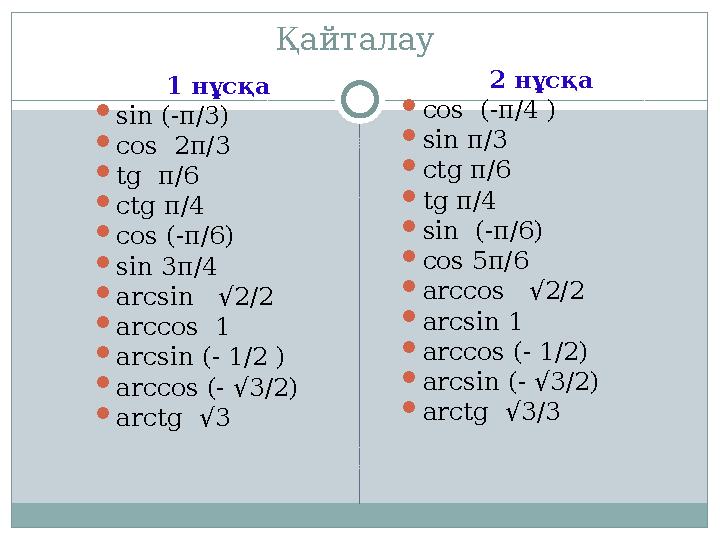
Қайталау 1 нұсқа sin (-π/3) cos 2π/3 tg π/6 ctg π/4 cos (-π/6) sin 3π/4 arcsin √2/2 arccos 1 arcsin (- 1/2 ) arccos (- √3/2) arctg √3 2 нұсқа cos (-π/4 ) sin π/3 ctg π/6 tg π/4 sin (-π/6) cos 5π/6 arccos √2/2 arcsin 1 arccos (- 1/2) arcsin (- √3/2) arctg √3/3

4 слайд

5 слайд
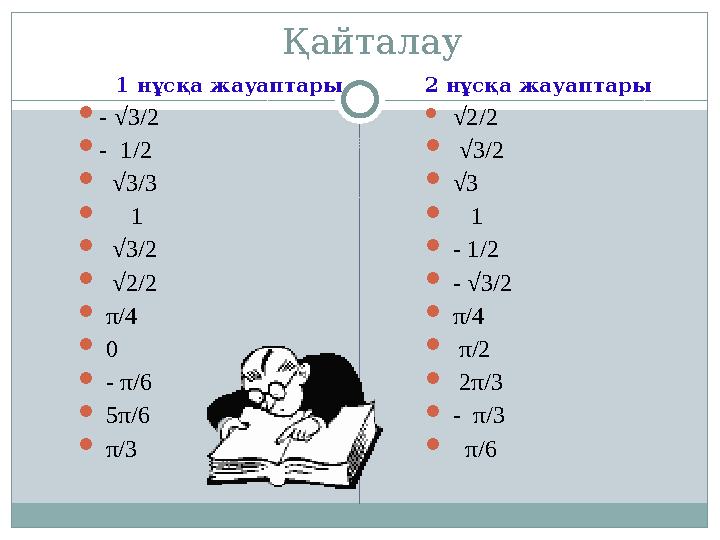
Қайталау 1 нұсқа жауаптары - √3/2 - 1/2  √3/3  1  √3/2  √2/2  π/4  0  - π/6  5π/6  π/3 2 нұсқа жауаптары  √2/2  √3/2  √3  1  - 1/2  - √3/2  π/4  π/2  2π/3  - π/3  π/6

5 слайд

6 слайд
Қарапайым тригонометриялық теңдеулердің түбірлерінің формулалары Қарапайым тригонометриялық теңдеулердің түбірлерінің формулалары 1. cost = а , мұндағы |а| ≤ 1 1. cost = а , мұндағы |а| ≤ 1 немесе Дербес жағдайлар1) cost=0 t = +πk‚ kЄZ 2) cost=1 t = 2πk‚ kЄZ 3) cost = -1 t = π+2πk‚ kЄZ 2 

6 слайд

7 слайд
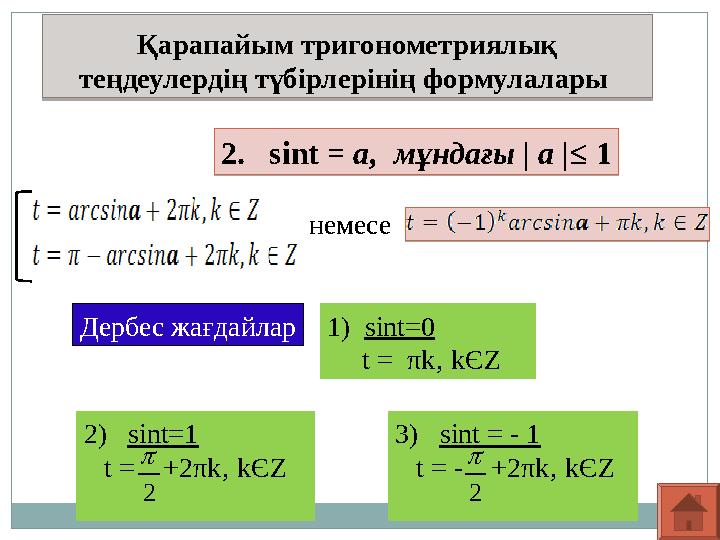
Қарапайым тригонометриялық теңдеулердің түбірлерінің формулалары Қарапайым тригонометриялық теңдеулердің түбірлерінің формулалары 2. sint = а, мұндағы | а |≤ 1 2. sint = а, мұндағы | а |≤ 1 немесе Дербес жағдайлар1) sint=0 t = πk‚ kЄZ 2) sint=1 t = +2πk‚ kЄZ 3) sint = - 1 t = - +2πk‚ kЄZ 2  2 

7 слайд

8 слайд
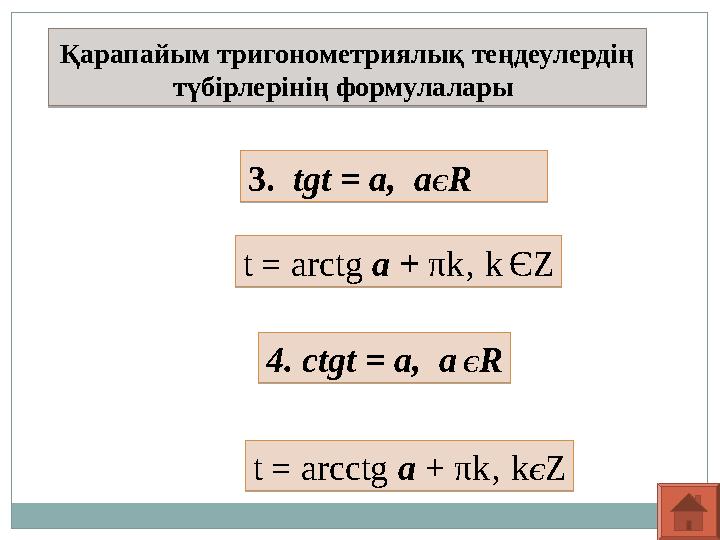
Қарапайым тригонометриялық теңдеулердің түбірлерінің формулалары Қарапайым тригонометриялық теңдеулердің түбірлерінің формулалары 3. tgt = а, аЄR 3. tgt = а, аЄR t = arctg а + πk‚ k ЄZ t = arctg а + πk‚ k ЄZ4. ctgt = а, а ЄR 4. ctgt = а, а ЄRt = arcctg а + πk‚ kЄZ t = arcctg а + πk‚ kЄZ

8 слайд

9 слайд
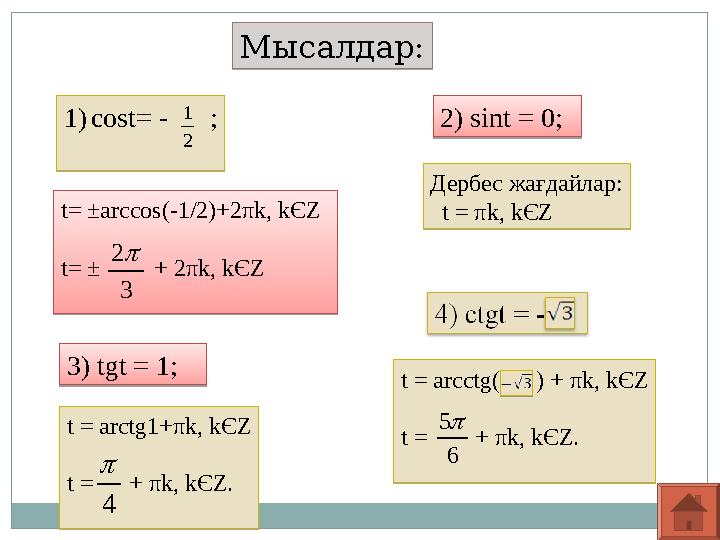
Мысалдар: Мысалдар:1)cost= - ; 1)cost= - ;2) sint = 0; 2) sint = 0;3) tgt = 1; 3) tgt = 1;t= ±arccos(-1/2)+2πk, kЄZ t= ± + 2πk, kЄZ t= ±arccos(-1/2)+2πk, kЄZ t= ± + 2πk, kЄZДербес жағдайлар: t = πk, kЄZ Дербес жағдайлар: t = πk, kЄZt = arctg1+πk, kЄZ t = + πk, kЄZ. t = arctg1+πk, kЄZ t = + πk, kЄZ.t = arcctg( ) + πk, kЄZ t = + πk, kЄZ. t = arcctg( ) + πk, kЄZ t = + πk, kЄZ. 3 2 6 5 4  2 1

9 слайд

10 слайд
Қарапайым теңдеулерді шешу Қарапайым теңдеулерді шешу1)tg2x = -1 2x = arctg (-1) + πk, kЄZ 2x = -π/4 + πk, kЄZ x = -π/8 + πk/2, kЄZ Жауабы: -π/8 + πk/2, kЄZ. 1)tg2x = -1 2x = arctg (-1) + πk, kЄZ 2x = -π/4 + πk, kЄZ x = -π/8 + πk/2, kЄZ Жауабы: -π/8 + πk/2, kЄZ.2) cos(x+π/3) = ½ x+π/3 = ±arccos1/2 + 2πk, kЄZ x+π/3 = ±π/3 + 2πk, kЄZ x = -π/3 ± π/3 + 2πk, kЄZ Жауабы: -π/3 ± π/3 + 2πk, kЄZ 2) cos(x+π/3) = ½ x+π/3 = ±arccos1/2 + 2πk, kЄZ x+π/3 = ±π/3 + 2πk, kЄZ x = -π/3 ± π/3 + 2πk, kЄZ Жауабы: -π/3 ± π/3 + 2πk, kЄZ3) sin(π – x/3) = 0 келтіру формуласы бойынша ықшамдаймыз sin(x/3) = 0 дербес жағдай x/3 = πk, kЄZ x = 3πk, kЄZ. Жауабы: 3πk, kЄZ. 3) sin(π – x/3) = 0 келтіру формуласы бойынша ықшамдаймыз sin(x/3) = 0 дербес жағдай x/3 = πk, kЄZ x = 3πk, kЄZ. Жауабы: 3πk, kЄZ.

10 слайд

11 слайд
Тригонометриялық теңдеулердің түрлері Тригонометриялық теңдеулердің түрлері1. Алгебралық теңдеулерге келтірілетін жаңа айнымалыны енгізу тәсілімен шешіледі a∙sin²x + b∙sinx + c=0 sinx = p деп белгілейік, мұндағы |p| ≤1, онда a∙p² + b∙p + c = 0 Түбірлерін тауып, алмастыруға қайтып келіп, қарапайым тригонометриялық теңдеуді шешу. 1. Алгебралық теңдеулерге келтірілетін жаңа айнымалыны енгізу тәсілімен шешіледі a∙sin²x + b∙sinx + c=0 sinx = p деп белгілейік, мұндағы |p| ≤1, онда a∙p² + b∙p + c = 0 Түбірлерін тауып, алмастыруға қайтып келіп, қарапайым тригонометриялық теңдеуді шешу. 2sin²x - 3sin x +1=0; Шешуі: sin x = t; 2t²-3t+1 = 0; D= (-3)² - 4·2·2 = 9 + 16 = 25 =5² ; t1,2= (3±5)/4; t1 = 2 ; t2 =0,5 ; sin x =2 шешімі жоқ, себебі 2 саны [-1;1] кесіндісіне жатпайды. sin x = 0,5 ; x = (-1) arcsin 0,5 + πn , n ЄZ; x = (-1) π/6 + πn , n ЄZ. Жауабы: x = (-1) π/6 + πn , n ЄZ. Мысал:

11 слайд

12 слайд
2. Біртекті теңдеулер 1)Бірінші дәрежелі: cos х (немесе sinx) бөлу арқылы және жаңа айнымалы енгізу арқылы шешіледі . a∙sinx + b∙cosx = 0 Қарапайым теңдеуді аламыз: a∙tgx + b = 0 немесе tgx = m 2. Біртекті теңдеулер 1)Бірінші дәрежелі: cos х (немесе sinx) бөлу арқылы және жаңа айнымалы енгізу арқылы шешіледі . a∙sinx + b∙cosx = 0 Қарапайым теңдеуді аламыз: a∙tgx + b = 0 немесе tgx = mТригонометриялық теңдеулердің түрлері Тригонометриялық теңдеулердің түрлері sinx + 2cosx = 0. Шешуі: теңдеудің екі жағын cosx бөлеміз. Жауабы:     kkarctgx tgx tgx x x x x ,2 2 02 0 cos cos 2 cos sin   kkarctg ,2 Мысал:

12 слайд

13 слайд
2) Екінші дәрежелі біртекті теңдеулер: cos х (немесе sinx) бөлу арқылы және жаңа айнымалы енгізу арқылы шешіледі . a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0 Екі жағын cos²x –ке бөлеміз. Квадрат теңдеу аламыз: a∙tg²x + b∙tgx + c = 0. 2) Екінші дәрежелі біртекті теңдеулер: cos х (немесе sinx) бөлу арқылы және жаңа айнымалы енгізу арқылы шешіледі . a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0 Екі жағын cos²x –ке бөлеміз. Квадрат теңдеу аламыз: a∙tg²x + b∙tgx + c = 0.Тригонометриялық теңдеулердің түрлері Тригонометриялық теңдеулердің түрлері 3sin  2  x + 4 sin x · cos x + 5 cos  2  x = 2.   Шешуі:  3sin  2  x + 4 sin x · cos x + 5 cos  2  x = 2sin  2  x + 2cos  2  x ,             sin  2  x + 4 sin x · cos x + 3 cos  2  x = 0 ,             tg 2  x + 4 tg x + 3 = 0 ,  бұдан  y  2  + 4y +3 = 0 ,           бұл теңдеудің түбірлері:  y 1  = -1,  y 2  = -3,  бұдан                            1)   tg x = –1,  2)   tg x = –3, Жауабы:  nnarctgkk ,3;, 4   Мысал:

13 слайд

14 слайд
3. Тригонометриялық формулаларды түрлендіру жолымен шешілетін тригонометриялық теңдеулер: 3. Тригонометриялық формулаларды түрлендіру жолымен шешілетін тригонометриялық теңдеулер:    sin   x  + cos  x  = 1 .      Ш е ш у і.    Барлық мүшелерін сол жаққа ауыстырамыз:                             sin   x  + cos  x  – 1 = 0 ,Тригонометриялық теңдеулердің түрлері Тригонометриялық теңдеулердің түрлері немесе Шешімі жоқ t g arct g

14 слайд

15 слайд
4. Қосымша бұрыш енгізу арқылы шығарылатын тригонометриялық теңдеулер 4. Қосымша бұрыш енгізу арқылы шығарылатын тригонометриялық теңдеулерТригонометриялық теңдеулердің түрлері Тригонометриялық теңдеулердің түрлері а sinx + b cosx = c

15 слайд

16 слайд

16 слайд

17 слайд
5. Әмбебап алмастыруды қолдану арқылы шығарылатын тригонометриялық теңдеулер Қосымша аргумент енгізу арқылы шығарылады 5. Әмбебап алмастыруды қолдану арқылы шығарылатын тригонометриялық теңдеулер Қосымша аргумент енгізу арқылы шығарылады А sinx + B cosx = C Тексеру Егер , - дұрыс емес, онда , берілген теңдеудің түбірі болмайды Жауабы: Тригонометриялық теңдеулердің түрлері Тригонометриялық теңдеулердің түрлері

17 слайд

18 слайд

18 слайд

19 слайд
6. Дәрежені төмендету арқылы шығарылатын тригонометриялық теңдеулер 6. Дәрежені төмендету арқылы шығарылатын тригонометриялық теңдеулер

19 слайд

20 слайд
; 2 tg1 2 x 2tg sinx 2x   ; 2 tg1 2 x tg-1 cosx 2 2 x   ; 2 tg1 2 x 2tg tgx 2x   Формулалар. ;a 22 bС  ; С а ; b С a cosx +b sinx алмастырамыз C sin(x+), мұндағы sin = cos =  - қосымша бұрыш (аргумент). Әмбебап алмастыру. х   + 2n; Тексеру міндетті! Дәрежені төмендету. 2 2cos1 cos 2 x x   2 21 sin 2 xсos x   Қосымша бұрыш енгізу әдісі.

20 слайд

21 слайд
Ереже. Квадратты көрсең, дәрежесін төмендет. Көбейтіндіні көрсең, қосындыға келтір. Қосындыны көрсең, көбейтіндіге келтір.

21 слайд

22 слайд
1-нұсқа. «3»-ке 3 sin x+ 5 cos x = 0 5 sin 2 х - 3 sinх cos х - 2 cos 2 х =0 «4»-ке 3 cos 2 х + 2 sin х cos х =0 5 sin 2 х + 2 sinх cos х - cos 2 х =1 «5»-ке 2 sin x - 5 cos x = 3 1- 4 sin 2x + 6 cos 2 х = 0 2-нұсқа. «3»-ке  cos x+ 3 sin x = 0 6 sin 2 х - 5 sinх cos х + cos 2 х =0 «4»-ке 2 sin 2 x – sin x cosx =0 4 sin 2 х - 2sinх cos х – 4 cos 2 х =1 «5»-ке 2 sin x - 3 cos x = 4 2 sin 2 х - 2sin 2х +1 =0

22 слайд