Материалдар / Презентация "Тригонометриялық теңсіздіктерді шешу" 10 сынып

Презентация "Тригонометриялық теңсіздіктерді шешу" 10 сынып

Материал туралы қысқаша түсінік

Жаңа тақырыпты игеруде бірлік шеңберде тригонометриялық теңсіздіктерді шешуді слайдпен көрсету түсінікті, тиімді

Карыбаева Сауле Шешкеновна

13 Маусым 2018

4910

16 рет жүктелген

Алгебра Презентация 10 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 11

Материал жариялап, аттестацияға 100% жарамды сертификатты тегін алыңыз!

Ustaz tilegi журналы министірліктің тізіміне енген. Qr коды мен тіркеу номері беріледі. Материал жариялаған соң сертификат тегін бірден беріледі.

Оқу-ағарту министірлігінің ресми жауабы

Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!

Қазақстан Республикасының білім беру жүйесін дамытуға қосқан жеке үлесі үшін және де Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық материалыңызбен бөлісіп, белсенді болғаныңыз үшін алғыс білдіреміз!

Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!

Тәуелсіз Қазақстанның білім беру жүйесін дамытуға және білім беру сапасын арттыру мақсатында Республика деңгейінде «Ustaz tilegi» Республикалық ғылыми – әдістемелік журналының желілік басылымына өз авторлық жұмысын жариялағаны үшін марапатталасыз!

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд
1) sin x < a, sin x > a, sin x ≥ a, sin x ≤ a 2) cos x < a, cos x > a, cos x ≥ a, cos x ≤ a 3) tg x < a, tg x > a, tg x ≥ a, tg x ≤ a 4) ctg x < a, ctg x > a, ctg x ≥ a, ctg x ≤ a

2 слайд

1) sin x < a, sin x > a, sin x ≥ a, sin x ≤ a 2) cos x < a, cos x > a, cos x ≥ a, cos x ≤ a 3) tg x < a, tg x > a, tg x ≥ a, tg x ≤ a 4) ctg x < a, ctg x > a, ctg x ≥ a, ctg x ≤ a

3 слайд
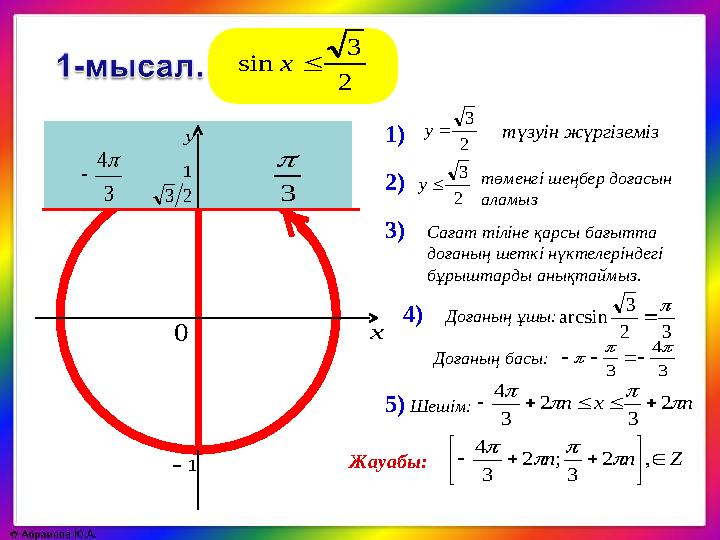
32 3 arcsin   түзуін жүргіземіз nxn     2 3 2 3 4  Znn         ,2 3 ;2 3 4     1) 2) 5) Сағат тіліне қарсы бағытта доғаның шеткі нүктелеріндегі бұрыштарды анықтаймыз. Доғаның басы: Доғаның ұшы: 3 4 3    4) Шешім: 3  23 0 х у 1 3 4  1 2 3 у Жауабы: төменгі шеңбер доғасын аламыз2 3 у 3) 2 3 sinx

3 слайд

32 3 arcsin   түзуін жүргіземіз nxn     2 3 2 3 4  Znn         ,2 3 ;2 3 4     1) 2) 5) Сағат тіліне қарсы бағытта доғаның шеткі нүктелеріндегі бұрыштарды анықтаймыз. Доғаның басы: Доғаның ұшы: 3 4 3    4) Шешім: 3  23 0 х у 1 3 4  1 2 3 у Жауабы: төменгі шеңбер доғасын аламыз2 3 у 3) 2 3 sinx

4 слайд
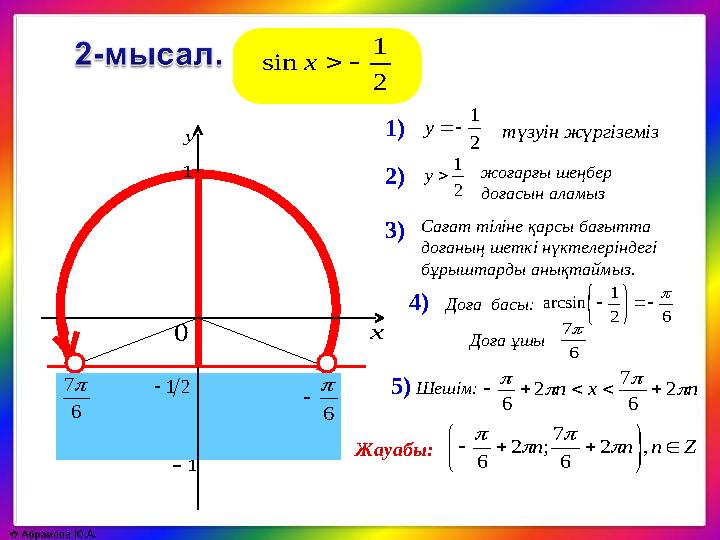
2 1 sinx 62 1 arcsin         түзуін жүргіземіз nxn     2 6 7 2 6  1) 2) 5) Сағат тіліне қарсы бағытта доғаның шеткі нүктелеріндегі бұрыштарды анықтаймыз. Доға ұшы Доға басы: 6 7 4) Шешім: 6   21 0 х у 1 6 7 1 2 1 у Жауабы: жоғарғы шеңбер доғасын аламыз2 1 у 3) Znnn        ,2 6 7 ;2 6    

4 слайд

2 1 sinx 62 1 arcsin         түзуін жүргіземіз nxn     2 6 7 2 6  1) 2) 5) Сағат тіліне қарсы бағытта доғаның шеткі нүктелеріндегі бұрыштарды анықтаймыз. Доға ұшы Доға басы: 6 7 4) Шешім: 6   21 0 х у 1 6 7 1 2 1 у Жауабы: жоғарғы шеңбер доғасын аламыз2 1 у 3) Znnn        ,2 6 7 ;2 6    

5 слайд
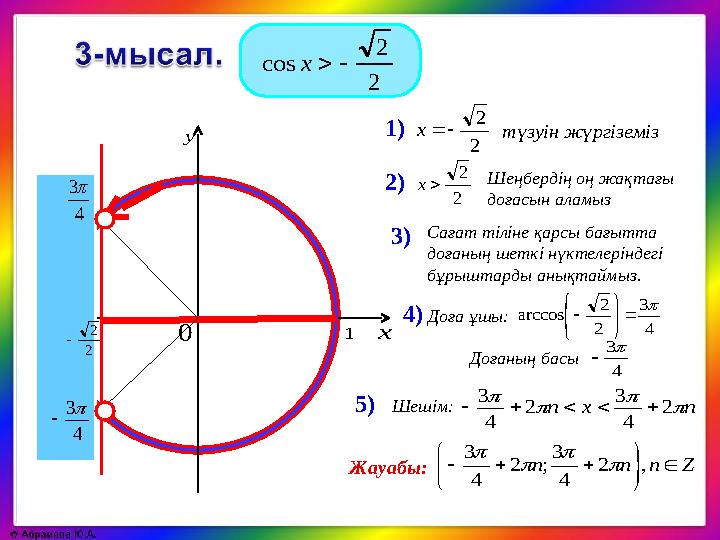
1 2 2 cosx 4 3 2 2 arccos            түзуін жүргіземіз nxn     2 4 3 2 4 3  1) 2) 5) Сағат тіліне қарсы бағытта доғаның шеткі нүктелеріндегі бұрыштарды анықтаймыз. Доғаның басы Доға ұшы: 4 3  4) Шешім: 0 х у 1 2 2 x Жауабы: Шеңбердің оң жақтағы доғасын аламыз2 2 x 3) Znnn        ,2 4 3 ;2 4 3     4 3  2 2  4 3

5 слайд

1 2 2 cosx 4 3 2 2 arccos            түзуін жүргіземіз nxn     2 4 3 2 4 3  1) 2) 5) Сағат тіліне қарсы бағытта доғаның шеткі нүктелеріндегі бұрыштарды анықтаймыз. Доғаның басы Доға ұшы: 4 3  4) Шешім: 0 х у 1 2 2 x Жауабы: Шеңбердің оң жақтағы доғасын аламыз2 2 x 3) Znnn        ,2 4 3 ;2 4 3     4 3  2 2  4 3

6 слайд
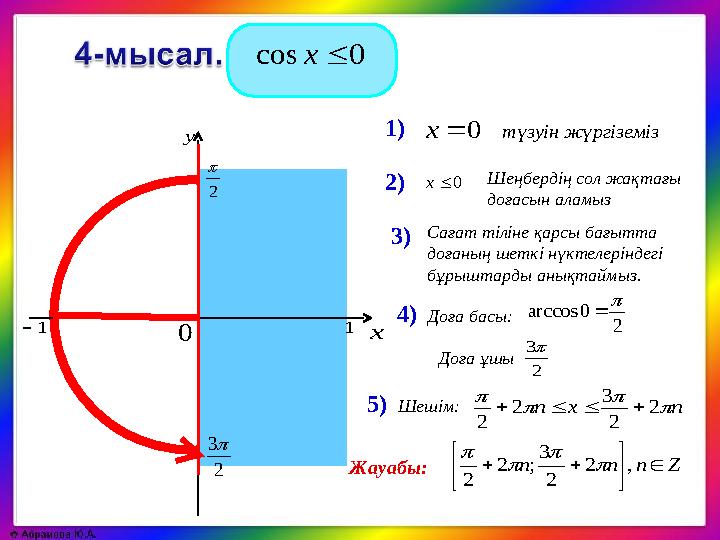
0cosx 2 0arccos   түзуін жүргіземіз nxn     2 2 3 2 2  1) 2) 5) Сағат тіліне қарсы бағытта доғаның шеткі нүктелеріндегі бұрыштарды анықтаймыз. Доға ұшы Доға басы: 2 3 4) Шешім: 2 3 0 х у 1 2  1 0x Шеңбердің сол жақтағы доғасын аламыз 0x 3) Znnn         ,2 2 3 ;2 2     Жауабы:

6 слайд

0cosx 2 0arccos   түзуін жүргіземіз nxn     2 2 3 2 2  1) 2) 5) Сағат тіліне қарсы бағытта доғаның шеткі нүктелеріндегі бұрыштарды анықтаймыз. Доға ұшы Доға басы: 2 3 4) Шешім: 2 3 0 х у 1 2  1 0x Шеңбердің сол жақтағы доғасын аламыз 0x 3) Znnn         ,2 2 3 ;2 2     Жауабы:

7 слайд
р/с Теңсіздік Жауабы 1 2 3 4 5 6 2 2 sinx 2 1 sinx 0sinx 2 1 cosx 2 3 cosx 0cosx Znnn         ,2 6 ;2 6 5     Znnn         ,2 4 3 ;2 4     Znnn         ,2 6 5 ;2 6 5      Znnn  ,2;2  Znnn        ,2 3 5 ;2 3     Znnn        ,2 2 ;2 2    

7 слайд

р/с Теңсіздік Жауабы 1 2 3 4 5 6 2 2 sinx 2 1 sinx 0sinx 2 1 cosx 2 3 cosx 0cosx Znnn         ,2 6 ;2 6 5     Znnn         ,2 4 3 ;2 4     Znnn         ,2 6 5 ;2 6 5      Znnn  ,2;2  Znnn        ,2 3 5 ;2 3     Znnn        ,2 2 ;2 2    

8 слайд
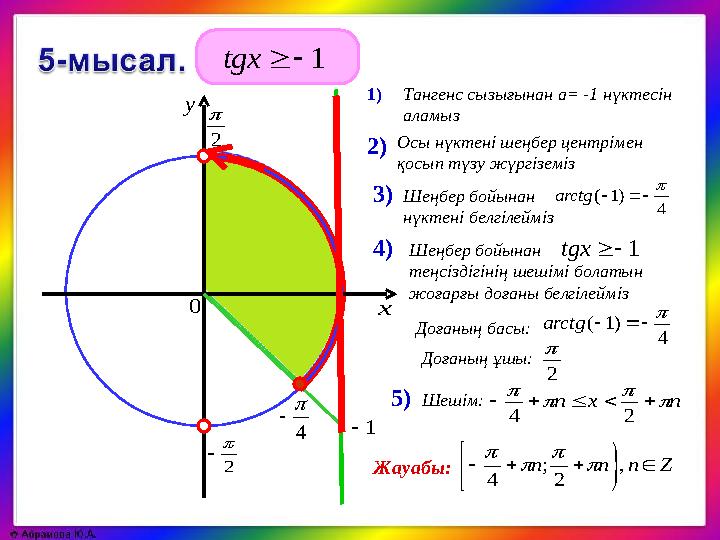
4   у 1tgx 4 )1(  arctg Тангенс сызығынан a= -1 нүктесін аламыз nxn      24 1) 2) 5) Доғаның ұшы: Доғаның басы: 2  4) Шешім: 4 )1(  arctg Осы нүктені шеңбер центрімен қосып түзу жүргіземіз 3) Znnn        , 2 ; 4     1 Шеңбер бойынан нүктені белгілейміз Шеңбер бойынан теңсіздігінің шешімі болатын жоғарғы доғаны белгілейміз 1tgx х Жауабы:2   0 2 

8 слайд

4   у 1tgx 4 )1(  arctg Тангенс сызығынан a= -1 нүктесін аламыз nxn      24 1) 2) 5) Доғаның ұшы: Доғаның басы: 2  4) Шешім: 4 )1(  arctg Осы нүктені шеңбер центрімен қосып түзу жүргіземіз 3) Znnn        , 2 ; 4     1 Шеңбер бойынан нүктені белгілейміз Шеңбер бойынан теңсіздігінің шешімі болатын жоғарғы доғаны белгілейміз 1tgx х Жауабы:2   0 2 

9 слайд
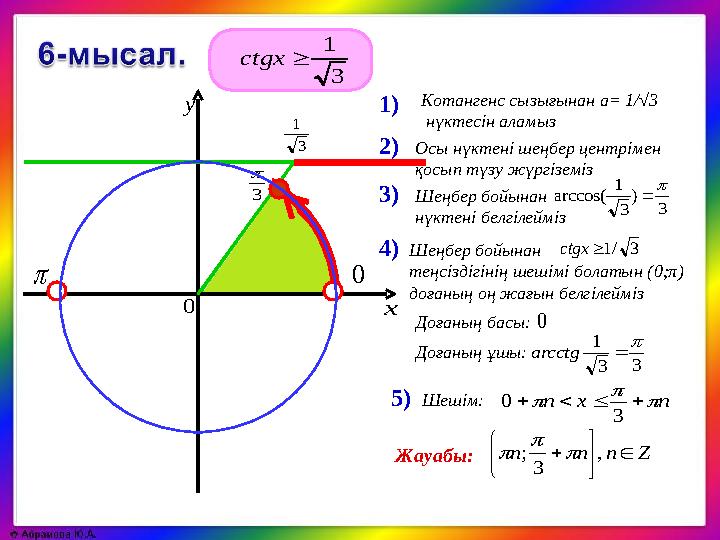
0 3  у 3 1 ctgx 3 ) 3 1 arccos(   Котангенс сызығынан a= 1/√3 нүктесін аламыз nxn     3 0 1) 2) 5) Доғаның ұшы: Доғаның басы: 33 1 arcctg 4) Шешім: 0 Осы нүктені шеңбер центрімен қосып түзу жүргіземіз 3) Znnn        , 3 ;   3 1 Шеңбер бойынан нүктені белгілейміз Шеңбер бойынан теңсіздігінің шешімі болатын (0;π) доғаның оң жағын белгілейміз 3/1ctgx х Жауабы:  0

9 слайд

0 3  у 3 1 ctgx 3 ) 3 1 arccos(   Котангенс сызығынан a= 1/√3 нүктесін аламыз nxn     3 0 1) 2) 5) Доғаның ұшы: Доғаның басы: 33 1 arcctg 4) Шешім: 0 Осы нүктені шеңбер центрімен қосып түзу жүргіземіз 3) Znnn        , 3 ;   3 1 Шеңбер бойынан нүктені белгілейміз Шеңбер бойынан теңсіздігінің шешімі болатын (0;π) доғаның оң жағын белгілейміз 3/1ctgx х Жауабы:  0

10 слайд
р/с Теңсіздік Жауабы 1 2 3 4 0tgx 3tgx 1ctgx 0ctgx Znn            2 , 3 Znnn        ,; 2   Znnn        ,; 4   Znn          2 ,

10 слайд

р/с Теңсіздік Жауабы 1 2 3 4 0tgx 3tgx 1ctgx 0ctgx Znn            2 , 3 Znnn        ,; 2   Znnn        ,; 4   Znn          2 ,

Презентация "Тригонометриялық теңсіздіктерді шешу" 10 сынып

Химия пәні

Тарих пәні

Биология пәні

Ағылшын тілі пәні

География пәні

Информатика пәні

Мектепке дейінгі білім беру

«Қазақ тілі» жəне «Қазақ əдебиеті»

Дене шынықтыру

Білім алушылардың білім сапасын арттыру

Инклюзивті білім беру