2024-2025 оқу жылына арналған
қысқа мерзімді сабақ жоспарларын
Жүктеп алғыңыз келеді ме?
ҚР Білім және Ғылым министірлігінің стандартымен жасалған
Презентация "Виет теоремасы"8-сынып
Материал туралы қысқаша түсінік
презентация
Авторы:
22 Желтоқсан 2017
2077
5 рет жүктелген
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 12
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
1
2
3
4
Көлдеңенінен:
1.Барлық қабырғалары тең төртбұрыш.
2.Теңдеудің түбірлерінің бар, жоғын анықтайтын белгі
қалай аталады?
3.Құрамында айнымалысы бар теңдік?
4.Бірінші коэффициенті 1- ге те теңдеу?
Ерекше тор көзден француз математигінің фамилиясын
оқисыз. Ол кім?
1 слайд
1 2 3 4 Көлдеңенінен: 1.Барлық қабырғалары тең төртбұрыш. 2.Теңдеудің түбірлерінің бар, жоғын анықтайтын белгі қалай аталады? 3.Құрамында айнымалысы бар теңдік? 4.Бірінші коэффициенті 1- ге те теңдеу? Ерекше тор көзден француз математигінің фамилиясын оқисыз. Ол кім?
2 слайд
к
вадрат
кирсид минант
уедтең
те і
к
л рілген
Көлдеңенінен:
1.Барлық қабырғалары тең төртбұрыш.
2.Теңдеудің түбірлерінің бар, жоғын анықтайтын белгі
қалай аталады?
3.Құрамында айнымалысы бар теңдік?
4.Бірінші коэффициенті 1- ге те теңдеу?
Ерекше тор көзден француз математигінің фамилиясын
оқисыз. Ол кім?
2 слайд
к вадрат кирсид минант уедтең те і к л рілген Көлдеңенінен: 1.Барлық қабырғалары тең төртбұрыш. 2.Теңдеудің түбірлерінің бар, жоғын анықтайтын белгі қалай аталады? 3.Құрамында айнымалысы бар теңдік? 4.Бірінші коэффициенті 1- ге те теңдеу? Ерекше тор көзден француз математигінің фамилиясын оқисыз. Ол кім?
3 слайд
7 желтоқсан
3 слайд
7 желтоқсан
4 слайд
Келтірілген квадрат
теңдеудің түбірлерінің
қосындысы
...........................................
.............., ал
түбірлерінің
көбейтіндісі
............................ тең.
Ф.Виет.
4 слайд
Келтірілген квадрат теңдеудің түбірлерінің қосындысы ........................................... .............., ал түбірлерінің көбейтіндісі ............................ тең. Ф.Виет.
5 слайд
Теңдеу авсх
1 х
2х
1 + х
2 х
1 х
2
х
2
–6х +8 = 01 -6 8 2 4 2+4=6 2·4=8
х
2
+ 2х -3= 0 12 -3 1 -3 1+(-3)=-2 1·(-3)=-3
х
2
– 5х + 6 = 0 1-5 6 2 3 2+3=5 2·3=6
5 слайд
Теңдеу авсх 1 х 2х 1 + х 2 х 1 х 2 х 2 –6х +8 = 01 -6 8 2 4 2+4=6 2·4=8 х 2 + 2х -3= 0 12 -3 1 -3 1+(-3)=-2 1·(-3)=-3 х 2 – 5х + 6 = 0 1-5 6 2 3 2+3=5 2·3=6
6 слайд
Виет теоремасы:
Келтірілген квадрат
теңдеудің түбірлерінің
қосындысы қарама-
қарсы таңбамен
алынған екінші
коэффициентке, ал
көбейтінділері бос
мүшеге тең.
6 слайд
Виет теоремасы: Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама- қарсы таңбамен алынған екінші коэффициентке, ал көбейтінділері бос мүшеге тең.
7 слайд
Келтірілген квадрат
теңдеудің түбірлерінің
қосындысы қарама қарсы
таңбамен алынған екінші
коэффициентке, ал
түбірлерінің көбейтіндісі
бос мүшеге тең.
Ф.Виет.
7 слайд
Келтірілген квадрат теңдеудің түбірлерінің қосындысы қарама қарсы таңбамен алынған екінші коэффициентке, ал түбірлерінің көбейтіндісі бос мүшеге тең. Ф.Виет.
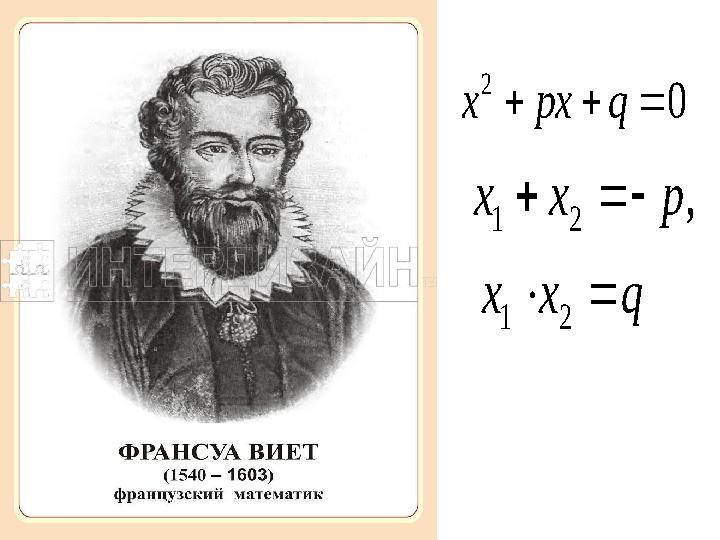
8 слайд
qxx
pхх
21
21
,
0
2
qpxх
8 слайд
qxx pхх 21 21 , 0 2 qpxх
9 слайд
x
2
-6х+5=0 x
1=3x
2=5
x
2
-х-30=0 x
1=0,4 x
2=0,2
x
2
-8х+15=0 x
1+x
2=6
x
1∙x
2=5
x
2
-0,6х+0,08=0 x
1=1,x
2=1
x
2
-2х+1=0 x
1+x
2=1
x
1∙x
2=-30
x
2
-10х+25=0 x
1=5,x
2=5
Сәйкестендіру
9 слайд
x 2 -6х+5=0 x 1=3x 2=5 x 2 -х-30=0 x 1=0,4 x 2=0,2 x 2 -8х+15=0 x 1+x 2=6 x 1∙x 2=5 x 2 -0,6х+0,08=0 x 1=1,x 2=1 x 2 -2х+1=0 x 1+x 2=1 x 1∙x 2=-30 x 2 -10х+25=0 x 1=5,x 2=5 Сәйкестендіру
10 слайд
10 слайд
11 слайд
Бүгінгі
сабақта
не ұнады?
11 слайд
Бүгінгі сабақта не ұнады?
