Материалдар / Қисық сызықты трапеция және оның ауданы 11 сынып

Қисық сызықты трапеция және оның ауданы 11 сынып

Материал туралы қысқаша түсінік

Қисық сызықты трапеция және оның ауданы 11 сынып презентация

Тулешова Назерке Ерболаткызы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

07 Қазан 2024

187

0 рет жүктелген

Алгебра Презентация 11 сынып

250 ₸

Бүгін алсаңыз
+13 бонус беріледі
Бұл не?

Бүгін алсаңыз +13 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 8

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Қисық сызықты трапеция және оның ауданы

1 слайд

Қисық сызықты трапеция және оның ауданы

2 слайд
Қисық сызықты трапеция жоғарыдан қисық , жандарынан абсциссалары және болатын нүктелердің ординаталары мен, ал төменнен өсінің кесіндісімен шектелген болса, ондай фигураның ауданы формуласы келесідей:   b a dxxfS )( )(xfy ax bx Ox

2 слайд

Қисық сызықты трапеция жоғарыдан қисық , жандарынан абсциссалары және болатын нүктелердің ординаталары мен, ал төменнен өсінің кесіндісімен шектелген болса, ондай фигураның ауданы формуласы келесідей:   b a dxxfS )( )(xfy ax bx Ox

3 слайд
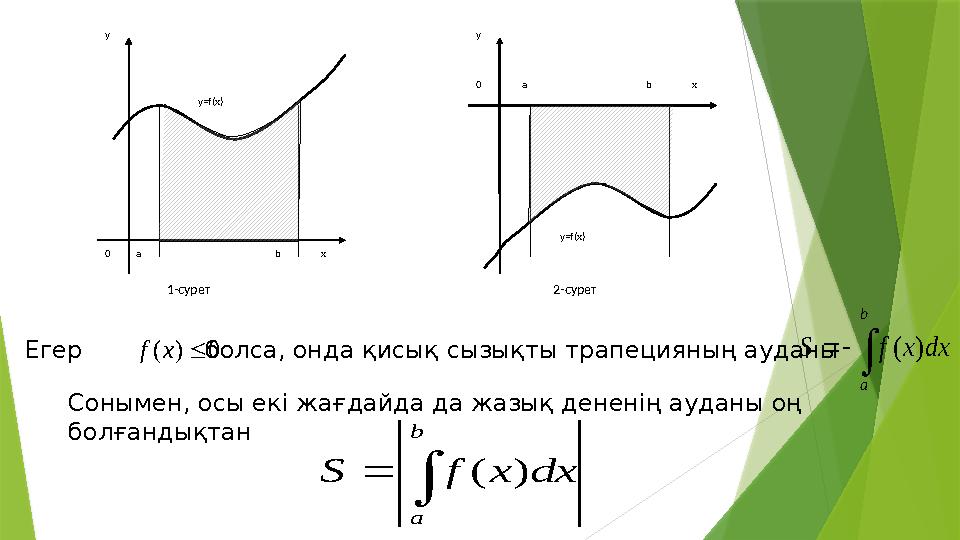
0 х у ba y=f(х) 1-сурет 0 х у ba y=f(х) 2-сурет 0)(xf Егер болса, онда қисық сызықты трапецияның ауданы   b a dxxfS )( Сонымен, осы екі жағдайда да жазық дененің ауданы оң болғандықтан   b a dxxfS )(

3 слайд

0 х у ba y=f(х) 1-сурет 0 х у ba y=f(х) 2-сурет 0)(xf Егер болса, онда қисық сызықты трапецияның ауданы   b a dxxfS )( Сонымен, осы екі жағдайда да жазық дененің ауданы оң болғандықтан   b a dxxfS )(

4 слайд
Егер функциясы аралығында таңбасын бірнеше рет өзгертетін болса, онда аралығын бөліктерге бөліп, функциясы таңбасы тұрақты әрбір аралықта жеке-жеке интегралдау керек : )(xf ba, ba, )(xf   b e e a d c с a b a dxxfdxxfdxxfdxxfdxxf )()()()()(

4 слайд

Егер функциясы аралығында таңбасын бірнеше рет өзгертетін болса, онда аралығын бөліктерге бөліп, функциясы таңбасы тұрақты әрбір аралықта жеке-жеке интегралдау керек : )(xf ba, ba, )(xf   b e e a d c с a b a dxxfdxxfdxxfdxxfdxxf )()()()()(

5 слайд
Егер жазық дене жоғарыдан және төменнен сәйкес және функцияларының графиктерімен шектелсе, онда оның ауданы болады )( 2 xf )( 1 xf     b a dxxfxfS )()( 12

5 слайд

Егер жазық дене жоғарыдан және төменнен сәйкес және функцияларының графиктерімен шектелсе, онда оның ауданы болады )( 2 xf )( 1 xf     b a dxxfxfS )()( 12

6 слайд
Жаңа сабақты бекіту Мысал-1. Гипербола түзулер және осімен шектелген фигураның ауданын есептеп шығару керек. Шешу: Берілген фигураның ауданын формулаға қойып есептейміз, яғни 4xy 4,1xx Ox 2ln8)1ln4(ln4ln4 4 4 1 4 1 4 1   xdx x ydxS

6 слайд

Жаңа сабақты бекіту Мысал-1. Гипербола түзулер және осімен шектелген фигураның ауданын есептеп шығару керек. Шешу: Берілген фигураның ауданын формулаға қойып есептейміз, яғни 4xy 4,1xx Ox 2ln8)1ln4(ln4ln4 4 4 1 4 1 4 1   xdx x ydxS

7 слайд