Қисық сызықты трапецияның ауданын табу.

1 слайд
Қисық сызықты трапеция және оның ауданы. № 11 Колледж Турсынбаев Бауыржан

1 слайд

2 слайд
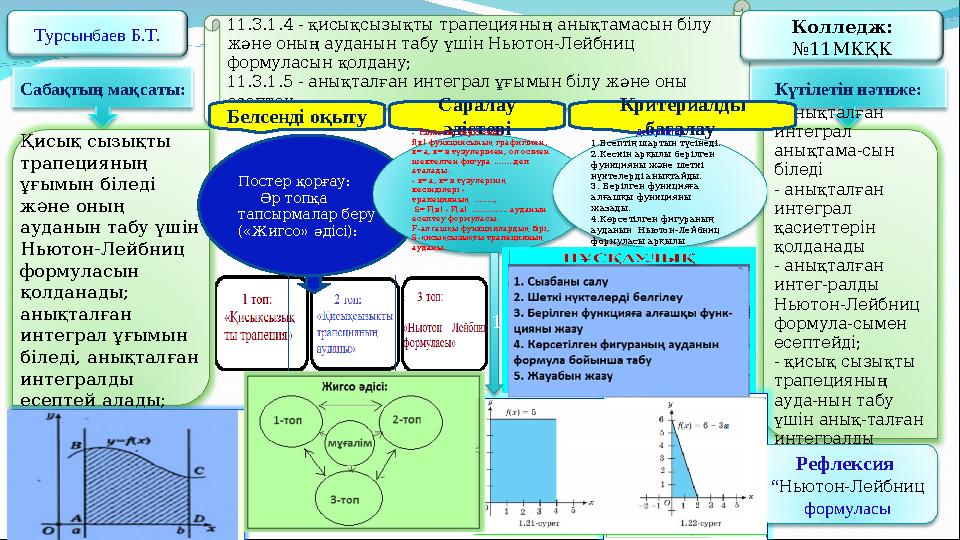
Турсынбаев Б.Т. 11.3.1.4 - қисықсызықты трапецияның анықтамасын білу және оның ауданын табу үшін Ньютон-Лейбниц формуласын қолдану; 11.3.1.5 - анықталған интеграл ұғымын білу және оны есептеу; Колледж: №11МКҚК Сабақтың мақсаты: Күтілетін нәтиже: Қисық сызықты трапецияның ұғымын біледі және оның ауданын табу үшін Ньютон-Лейбниц формуласын қолданады; анықталған интеграл ұғымын біледі, анықталған интегралды есептей алады; - анықталған интеграл анықтама-сын біледі - анықталған интеграл қасиеттерін қолданады - анықталған интег-ралды Ньютон-Лейбниц формула-сымен есептейді; - қисық сызықты трапецияның ауда-нын табу үшін анық-талған интегралды қолданады.Белсенді оқыту Саралау әдістері Критериалды бағалау Постер қорғау: Әр топқа тапсырмалар беру («Жигсо» әдісі): - Үзіліссіз, теріс емес f(х) функциясының графигімен, х=а, х=в түзулерімен, ол осімен шектелген фигура  ........ деп аталады. - х=a, х=в түзулерінің кесінділері - трапецияның ........, S=Ғ(в) - F(а) .............. ауданын есептеу формуласы. F-алғашқы функциялардың бірі, S-қисықсызықты трапецияның ауданы. Дескриптор 1.Есептің шартын түсінеді. 2.Кескін арқылы берілген функцияны және шеткі нүктелерді анықтайды. 3. Берілген функцияға алғашқы функцияны жазады. 4.Көрсетілген фигураның ауданын Ньютон-Лейбниц формуласы арқылы есептейді Рефлексия “ Ньютон-Лейбниц формуласы1

2 слайд

3 слайд
Сабақ барысы: 1.Ұйымдастыру: а) Оқушылармен амандасу; ә) Сыныпты топқа бөлу: 1 топ: «Қисықсызықты трапеция»; 2 топ: «Қисықсызықты трапецияның ауданы», 3 топ: «Ньютон—Лейбниц формуласы» б) Жағымды психологиялық ахуал тудыру: «Жылулық шеңбері» арқылы сабақты бастаймыз. Оқушылар бір –бірімен қол ұстасып, өз тілектерін айтып, жылулықты бір – біріне алақандары арқылы береді де, аудиторияға қарай «суф» дейді.. 2. Өткен тақырыпты қайталау . 1. Алғашқы функция дегеніміз не? 2. Туынды мен алғашқы функция арасында байланыс бар ма? 3. Алғашқы функцияның негізгі қасиеті қандай? 4. Алғашқы функциялардын қасиетін айт. 5. Алғашқы функцияларды табу ерекшелігін қолдану. 3. І. Сабақтың табыс критериін анықтау: - анықталған интеграл анықтамасын білемін -анықталған интеграл қасиеттерін қолдана аламын - қисық сызықты трапецияның ауданын таба аламын - есеп шығаруда қолдана аламын ІІ . Постер қорғау: Әр топқа тапсырмалар беру(«Жигсо» әдісі): 1 топ: «Қисықсызықты трапеция»; 2 топ: «Қисықсызықты трапецияның ауданы», 3 топ: «Ньютон—Лейбниц формуласы» ІІІ. Талдау: жұпта, топта

3 слайд

4 слайд
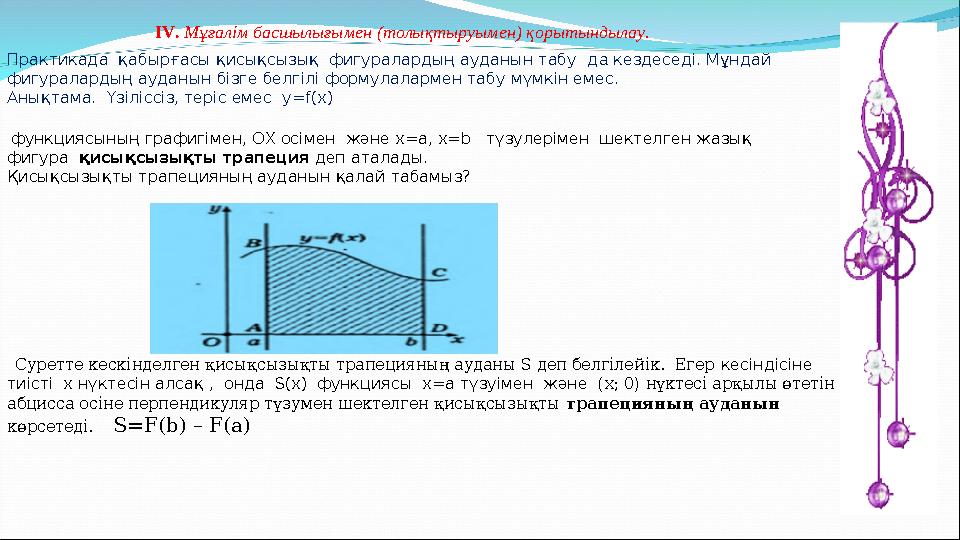
ІV. Мұғалім басшылығымен (толықтыруымен) қорытындылау. Практикада қабырғасы қисықсызық фигуралардың ауданын табу д a кездеседі. Мұндай фигуралардың ауданын бізге белгілі формулалармен табу мүмкін емес. Анықтама. Үзіліссіз, теріс емес y=f(x) функциясының графигімен, ОХ осімен және х=а, х=b түзулерімен шектелген жазық фигура қисықсызықты трапеция деп аталады. Қисықсызықты трапецияның ауданын қалай табамыз? Суретте кескінделген қисықсызықты трапецияның ауданы S деп белгілейік. Егер кесіндісіне тиісті х нүктесін алсақ , онда S(х) функциясы х=а түзуімен және (x ; 0) нүктесі арқылы өтетін абцисса осіне перпендикуляр түзумен шектелген қисықсызықты трапецияның ауданын көрсетеді. S=F(b) – F(a)

4 слайд

5 слайд
Қисықсызықты трапецияның ауданын табу үшін келесі алгоритм қолданылады. • Графигі қисықсызықты трапеция жоғарыдан шектейтін функцияның алғашқы функцияларының бірін табамыз. • Қисықсызықты трапецияның төменгі табаны болатын кесіндінің шеткі нүктелерінің координаталарын анықтаймыз. • Формула бойынша қисықсызықты трапецияның ауданын табамыз. • Бір координаталық жазықтыққа берілген қисықтардың графиктерін саламыз. Мысал 1 x=2 , x=3, у=0 және f(x)=x – 2x – 1 сызықтарымен шектелген қисықсызықты трапецияның ауданын табыңыз. Алдымен параболаның графигін саламыз. Содан кейін x=2 , x=3 түзулерін саламыз. 2

5 слайд

6 слайд
V. а) Есептер шығару: 1 топ: №1,69 1.21, 1.22-суреттерде көрсетілген фигуралардың ауданын геометриялық жолмен және анықталған интеграл арқылы есептеңдер: Дескриптор: 1.Есептің шартын түсінеді. 2.Кескін арқылы берілген функцияны және шеткі нүктелерді анықтайды. 3. Берілген функцияға алғашқы функцияны жазады. 4.Көрсетілген фигураның ауданын Ньютон-Лейбниц формуласы арқылы есептейді 5. Жауабын жазады. 2 топ: №1,70 1.23, 1.24-суреттерде көрсетілген қисықсызықты трапецияның ауданын анықталған интеграл арқылы өрнектеп, есептеңдер: Дескриптор: 1.Есептің шартын түсінеді. 2.Кескін арқылы берілген функцияны және шеткі нүктелерді анықтайды. 3. Берілген функцияға алғашқы функцияны жазады. 4.Көрсетілген фигураның ауданын Ньютон-Лейбниц формуласы арқылы есептейді 5. Жауабын жазады 3 топ: №1,71 1.25—1.27-суреттерде кескінделген қисықсызықты трапецияның ауданын анықталған интеграл арқылы жазып есептеңдер: Дескриптор: 5. Жауабын жазады 1.Есептің шартын түсінеді. 2.Кескін арқылы берілген функцияны және шеткі нүктелерді анықтайды. 3. Берілген функцияға алғашқы функцияны жазады. 4.Көрсетілген фигураның ауданын Ньютон-Лейбниц формуласы арқылы есептейді

6 слайд

7 слайд
В) Мұғалім басшылығымен: № 1,79 және №1,80 Дескриптор: 1.Есептің шартын түсінеді 2. Есептің берілгені бойынша сызбасын салады 3.Шыққан фигураның ауданын интеграл арқылы есептейді 4. Интегралдың шектерін дұрыс қояды 5. Ньютон-Лейбниц формуласын пайдаланып есептейді 4. Кері байланыс. Бір ауыз сөз. Сабақтың мақсатына жеттік пе? Неліктен олай ойлайсыздар? Сабақта ең маңызды не болды? Тақтада көрсетілген сәйкес бағанға стикер жабыстырады (аттарын жазып, өздерінің сабақты қалай түсінгенін немесе көңіл-күй деңгейін білдіреді). Алға қарай жылжуға әзірмін Кейбірін түсіндім, бірақ бәрін емес Түсінбедім, қайта қарап шығуым керек Келесі сабаққа тапсырма: № 1,81 Ньютон—Лейбниц формуласын қолданып, мына анықталған интегралды есептеңдер:

7 слайд

8 слайд

8 слайд