сабақ жоспары Квадрат үшмүшені көбейткіштерге жіктеу 8 сынып

1 слайд
Квадрат үшмүшені көбейткіштерге жіктеу 8 сынып

1 слайд

2 слайд
Оқу мақсаттары 8.2.1.3 квадрат үшмүшені көбейткіштерге жіктеу; Сабақ мақсаттары Оқушылар: Квадрат үшмүшенің түбірлерін таба алады ; Квадрат үшмүшеден екімүшенің квадратын бөліп алады . Квадрат үшмүшені көбейткіштерге жіктей алады

2 слайд

3 слайд
Сенің білетінің: • квадрат үшмүшеден екімүшенің толық квадратын бөліп алу жолы. Сенің меңгеретінің: • квадрат үшмүшеден екімүшенің толық квадратын бөліп алу. • квадрат үшмүшені көбейткіштерге жіктеу;

3 слайд

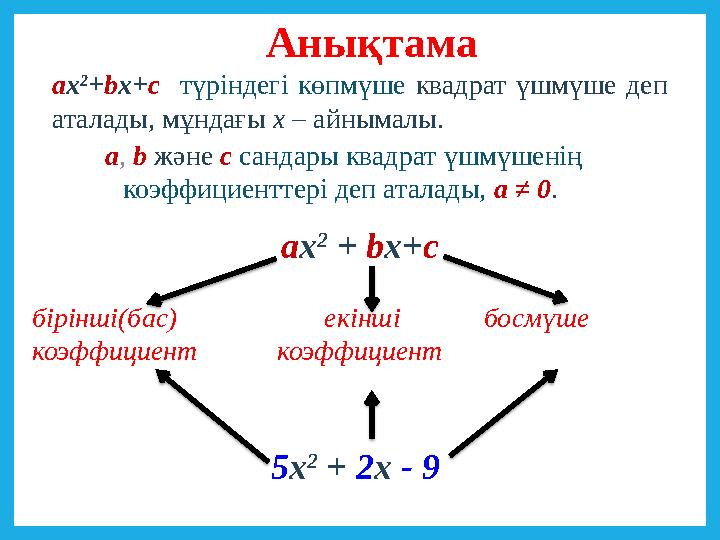
4 слайд
а х 2 + b x+ c бірінші(бас) екінші босмүше коэффициент коэффициент 5 х 2 + 2 x - 9 а х 2 + b x+ c түріндегі көпмүше квадрат үшмүше деп аталады, мұндағы х – айнымалы.Анықтама а , b және с сандары квадрат үшмүшенің коэффициенттері деп аталады, а ≠ 0 .

4 слайд

5 слайд
Тапсырма. Квадрат үшмүшенің түбірлерін табыңыз: 3х 2   – 2х – 5 Теңдеуді шешейік Сонда Ендеше, 3х 2   – 2х – 5 квадрат үшмүшесінің екі түбірі бар және .

5 слайд

6 слайд
Дәлелдеуі:2 2 . b c ax bx c a x x a a            1 2 1 2 , . b c x x x x a a    2 2 1 2 1 2 ( ( ) ) b c a x x a x x x x x x a a              2 1 2 1 2 ( ) a x x x x x x x     1 2 1 ( ( ) ( )) a x x x x x x      1 2 ( )( ). a x x x x   Квадрат үшмүшенің жіктелуі Теореманың дәлелдеуі неге негізделген?Теорема: Егер және ах 2 + bx+c түріндегі көпмүше квадрат үшмүшесінің түбірлері болса ,онда ах 2 + bx+c= a(x- ) ( ) . ах 2 + bx+c= a(x- ) ( ) .

6 слайд

7 слайд
Кері тұжырым да дұрыс: егер квадрат үшмүшені көбейткіштерге жіктеу мүмкін болса, онда оның түбірлері бар болады. Квадрат үшмүшенің жіктелуі болып келесі жазба аталады : ах 2  + b х + с = а(х – х 1 )(х – х 2 ), мұндағы х 1 , х 2 – квадрат үшмүшенің түбірлері. Егер квадрат үшмүшенің түбірлері бар болса, онда оны көбейткіштерге жіктеуге болады.

7 слайд

8 слайд
Теоремаға ескерту. Егер квадрат үшмүшесінің дискриминанты нөлге тең болса, яғни ( еселі түбір), онда дәлелденген формула мына түрде жазылады:2 2 1 ( ) . ax bx c a x x     Мысал. 4х 2  + 4х + 1 = 4 ( х + ) 2 х =

8 слайд

9 слайд
Теорема . Е гер квадрат үшмүшенің түбірлері болмаса, онда оны сызықтық көбейткіштерге жіктеуге болмайды. Дәлелдеуі: түбірлері жоқ болсын. болсын деп ұйғарайық, мұндағы k, m, p, q – қандай да бір сандар. , егер және . және - түбірлері және - түбірлері Қарама-қайшылық: шарт бойынша түбірлері жоқ.

9 слайд

10 слайд
Тапсырма. х 2  + 10х + 25. • D=-4ac = 10 2   -4=100 -100=0 • x= =5, х 2   +10 х + 25 =(x+5 Бөлшегін қысқартыңыз: = D=-4ac = 6 2   -4= 36 - 36 =0 D=-4ac = 5 2   -4=25 +24=49 x= = -3 , = = -3 , = =0,5 == Сыныпта №275 Үйге тапсырма І нұсқа № 27 5 (а,б), №27 6 (б) ІІ нұсқа № 27 5 (ә,в), №27 6 (в)

10 слайд

11 слайд
• Бүгін мен білдім … • Маған қызықты болды … • Маған қиын болды … • Мен ... тапсырмаларын орындадым . Сабақ қорытындысы

11 слайд