Шаманың ең үлкен және ең кіші мәнін іздеуге берілген стереометриялық есептер.
Шаманың ең үлкен және ең кіші мәнін іздеуге берілген стереометриялық есептер.


#1 слайд
Бидайық негізгі мектебі
Сабақтың тақырыбы : Шаманың ең
үлкен және ең кіші мәнін іздеуге
берілген стереометриялық
есептер.
Орындаған: Бахытова М.
1 слайд
Бидайық негізгі мектебі Сабақтың тақырыбы : Шаманың ең үлкен және ең кіші мәнін іздеуге берілген стереометриялық есептер. Орындаған: Бахытова М.
#2 слайд
Сабақтың мақсаты:
Білімділік: Дамытушылық :
Тәрбиелік:
Стереометрияны
оқыту барысында
танымдық
дербестікті
қалыптастыру мен
оқушыларды
таныстыру және
есептерде қолдана
білуге үйрету Оқушыларды
ұйымшылдыққа
жауапкершілікке,
ұқыптылыққа,
тез шешім
қабылдауға
үйрету Теориялық
білімін
практикада
қолдана білу
дағдысын
қалыптастыру,
ой-өрісін
дамыту
2 слайд
Сабақтың мақсаты: Білімділік: Дамытушылық : Тәрбиелік: Стереометрияны оқыту барысында танымдық дербестікті қалыптастыру мен оқушыларды таныстыру және есептерде қолдана білуге үйрету Оқушыларды ұйымшылдыққа жауапкершілікке, ұқыптылыққа, тез шешім қабылдауға үйрету Теориялық білімін практикада қолдана білу дағдысын қалыптастыру, ой-өрісін дамыту
#3 слайд
1
• Шаман
ың ең
үлкен
және
ең кіші
мәнін
іздеуге
берілге
н
стерео
метрия
лық
есе птер
.ЖОСПАРЫ
3 слайд
1 • Шаман ың ең үлкен және ең кіші мәнін іздеуге берілге н стерео метрия лық есе птер .ЖОСПАРЫ

#4 слайд
Ұ й ы м д а с т ы р у к е з е ң і :
Ө т к е н с а б а қ т ы қ а й т а л а у
Е с е п т е р ш ы ғ а р у
4 слайд
Ұ й ы м д а с т ы р у к е з е ң і : Ө т к е н с а б а қ т ы қ а й т а л а у Е с е п т е р ш ы ғ а р у
#5 слайд
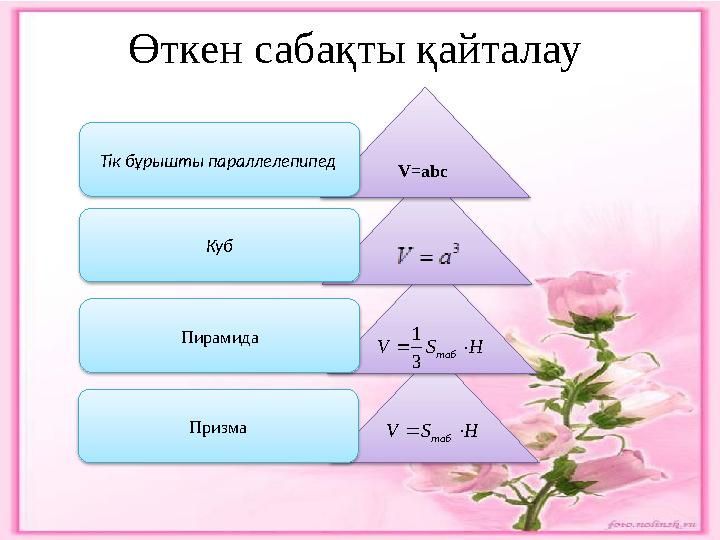
Өткен сабақты қайталау
V=abc Тік бұрышты параллелепипед
Куб
ПирамидаH S V таб
3
1
Призма
H S V таб
5 слайд
Өткен сабақты қайталау V=abc Тік бұрышты параллелепипед Куб ПирамидаH S V таб 3 1 Призма H S V таб
#6 слайд
Конус
Цилиндр
Шар
Шар сегментіH R V 2
3
1
H R V
2
3
3
4
R V
Шар секторы
h R h V
3
1 2
h R V
2
3
2
6 слайд
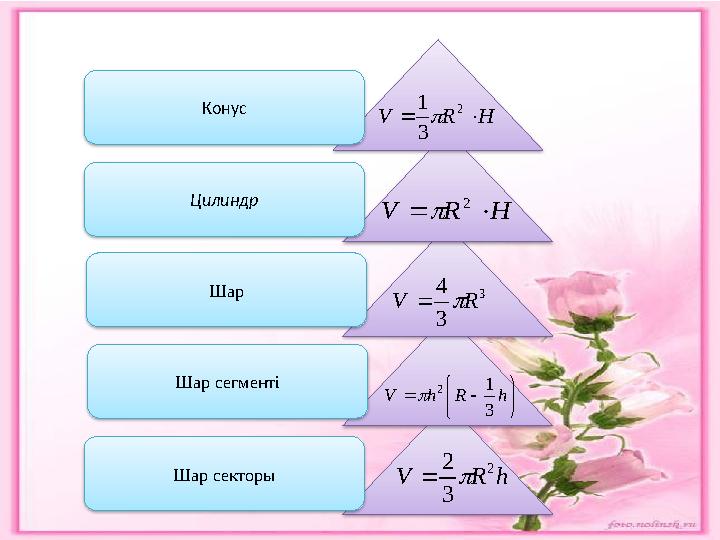
Конус Цилиндр Шар Шар сегментіH R V 2 3 1 H R V 2 3 3 4 R V Шар секторы h R h V 3 1 2 h R V 2 3 2

#7 слайд
10
Пирамида 20 30 40
Призма
Конус
Цилиндр 4030
20
10
2010
30 40
40302010
7 слайд
10 Пирамида 20 30 40 Призма Конус Цилиндр 4030 20 10 2010 30 40 40302010

#8 слайд
l P S б б
2
1
.Пирамиданың толық бетінің, бүйір бетінің
ауданы және көлемінің формуласы
Жауабы :
б б таб б т S S S . .
H S V таб
3
1
8 слайд
l P S б б 2 1 .Пирамиданың толық бетінің, бүйір бетінің ауданы және көлемінің формуласы Жауабы : б б таб б т S S S . . H S V таб 3 1

#9 слайд
l P S б б .Призманың толық бетінің, бүйір бетінің
ауданы және көлемінің формуласы
Жауабы :
б б таб б т S S S . .
H S V таб
9 слайд
l P S б б .Призманың толық бетінің, бүйір бетінің ауданы және көлемінің формуласы Жауабы : б б таб б т S S S . . H S V таб

#10 слайд
Конустың толық бетінің, бүйір бетінің
ауданы және көлемінің формуласы
Жауабы :б б таб б т S S S . .
H R V 2
3
1
RL S б б .
10 слайд
Конустың толық бетінің, бүйір бетінің ауданы және көлемінің формуласы Жауабы :б б таб б т S S S . . H R V 2 3 1 RL S б б .

#11 слайд
Цилиндрдің толық бетінің, бүйір бетінің
ауданы және көлемінің формуласы
Жауабы :RH S б б 2 .
) ( 2 2 2
2
. R H R R RH S б т
H R V
2
11 слайд
Цилиндрдің толық бетінің, бүйір бетінің ауданы және көлемінің формуласы Жауабы :RH S б б 2 . ) ( 2 2 2 2 . R H R R RH S б т H R V 2

#12 слайд
Пирамиданың табаны -параллелограмм, оның қабырғасы 3 см
және 7 см, ал диогональдарының бірі 6 см. Пирамиданың
биіктігі диогональдарының қиылысу нүктесінен өтеді, ол 4
см -ге тең. Бүйір қырын табыңыз.
AB=3, BC=7, AC=6, SH=4
SA -? Жауабы:
5 см
12 слайд
Пирамиданың табаны -параллелограмм, оның қабырғасы 3 см және 7 см, ал диогональдарының бірі 6 см. Пирамиданың биіктігі диогональдарының қиылысу нүктесінен өтеді, ол 4 см -ге тең. Бүйір қырын табыңыз. AB=3, BC=7, AC=6, SH=4 SA -? Жауабы: 5 см

#13 слайд
Табаны үшбұрыш болатын призманың
көлемі 42 , табан қабырғалары 3, 4,
5см-ке тең болса, биіктігін табыңдар
Жауабы: 7 см 3
см
13 слайд
Табаны үшбұрыш болатын призманың көлемі 42 , табан қабырғалары 3, 4, 5см-ке тең болса, биіктігін табыңдар Жауабы: 7 см 3 см

#14 слайд
2Конустың табанының радиусы 3 см, ал жасаушысы
табан жазықтығына 45 0
бұрыш жасай көлбеген.
Конустың көлемін және бүйір бетінің ауданын табыңыз .
2 18 S V
14 слайд
2Конустың табанының радиусы 3 см, ал жасаушысы табан жазықтығына 45 0 бұрыш жасай көлбеген. Конустың көлемін және бүйір бетінің ауданын табыңыз . 2 18 S V

#15 слайд
Жауабы :Цилиндрдің көлемі 112 см 3
, биіктігі 28 см. Осьтік
қимасының диогоналінің ұзындығын табыңыз.
15 слайд
Жауабы :Цилиндрдің көлемі 112 см 3 , биіктігі 28 см. Осьтік қимасының диогоналінің ұзындығын табыңыз.
#16 слайд
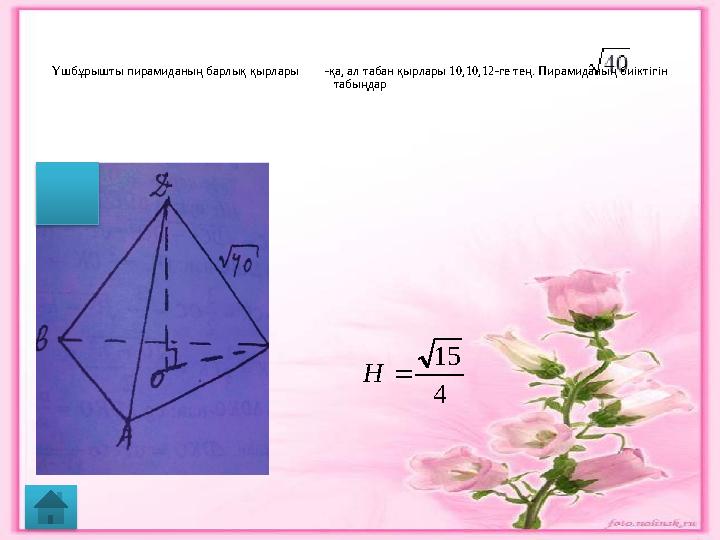
Үшбұрышты пирамиданың барлық қырлары -қа, ал табан қырлары 10,10,12-ге тең. Пирамиданың биіктігін
табыңдар4
15
H
16 слайд
Үшбұрышты пирамиданың барлық қырлары -қа, ал табан қырлары 10,10,12-ге тең. Пирамиданың биіктігін табыңдар4 15 H

#17 слайд
Құттықтаймыз!!!
17 слайд
Құттықтаймыз!!!
#18 слайд
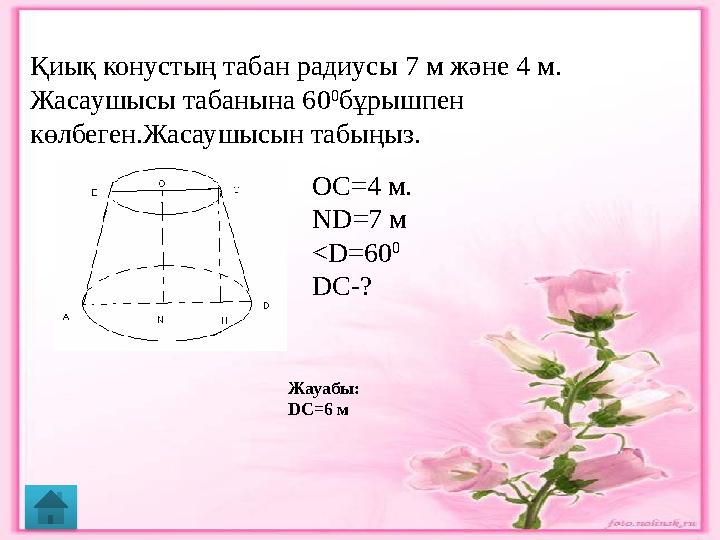
Қиық конустың табан радиусы 7 м және 4 м.
Жасаушысы табанына 60 0
бұрышпен
көлбеген.Жасаушысын табыңыз.
OC=4 м.
ND=7 м
<D=60 0
DC-?
Жауабы:
D C= 6 м
18 слайд
Қиық конустың табан радиусы 7 м және 4 м. Жасаушысы табанына 60 0 бұрышпен көлбеген.Жасаушысын табыңыз. OC=4 м. ND=7 м <D=60 0 DC-? Жауабы: D C= 6 м

#19 слайд
Цилиндрдің осьтік қимасының ауданы 70см 2
, ал биіктігі 7 см-ге тең. Цилиндрдің толық бетінің
ауданын табыңыз. 120
.
б т
S
19 слайд
Цилиндрдің осьтік қимасының ауданы 70см 2 , ал биіктігі 7 см-ге тең. Цилиндрдің толық бетінің ауданын табыңыз. 120 . б т S

#20 слайд
Үш бұрышты дұрыс пирамиданың биіктігі 40 см, табанының қабырғасы 10
см-ге тең. Табанының бір қырынан өтетін оған қарсы жатқан бүйір қырына
перпендикуляр қима жазықтық ауданын табыңдар 2
7
6
42 см
20 слайд
Үш бұрышты дұрыс пирамиданың биіктігі 40 см, табанының қабырғасы 10 см-ге тең. Табанының бір қырынан өтетін оған қарсы жатқан бүйір қырына перпендикуляр қима жазықтық ауданын табыңдар 2 7 6 42 см

#21 слайд
Дұрыс алты бұрышты ABCDEFA
1 B
1 C
1 D
1 E
1 F
1
призманың барлық қырлары 1-ге тең. Призманың F,
C, D
1 және Е
1 нүктелері арқылы өтетін қиманың
ауданын табыңыз4
7 3
21 слайд
Дұрыс алты бұрышты ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 призманың барлық қырлары 1-ге тең. Призманың F, C, D 1 және Е 1 нүктелері арқылы өтетін қиманың ауданын табыңыз4 7 3

#22 слайд
Қиық конустың осьтік қимасының диагоналы 17-ге, биіктігі 15-ке, ал
жасаушысының табан жазықтығына түскен проекциясы 2-ге тең. Қиық
конустың көлемңн табыңдар 245
22 слайд
Қиық конустың осьтік қимасының диагоналы 17-ге, биіктігі 15-ке, ал жасаушысының табан жазықтығына түскен проекциясы 2-ге тең. Қиық конустың көлемңн табыңдар 245

#23 слайд
Радиусы R, биіктігі Н-қа тең цилиндрге табаны
цилиндр табанының біріне іштей сызылған, ал
төбесі оның келесі табанына тиісті болатын дұрыс
төртбұрышты пирамида іштей сызылған.
Пирамиданың толық бетінің ауданын табыңыз.) 2 ( 2 2 2
. R R H R S б т
23 слайд
Радиусы R, биіктігі Н-қа тең цилиндрге табаны цилиндр табанының біріне іштей сызылған, ал төбесі оның келесі табанына тиісті болатын дұрыс төртбұрышты пирамида іштей сызылған. Пирамиданың толық бетінің ауданын табыңыз.) 2 ( 2 2 2 . R R H R S б т

#24 слайд
24 слайд

шағым қалдыра аласыз
















