санау жүйесі 7 сынып

1 слайд

1 слайд

2 слайд
Сандардың шығу тарихы Сандар шамамен 1500 жыл бұрынҮндістанда пайда болған Әуелі сандар сызықшамен белгіленген Н о ль санының пайда болуы сандарғареволюция жасаған «Қарыз», «жеткіліксіздік» деген ұғымдартеріс сандардың шығуына алып келеді

2 слайд

3 слайд
Сан түсінігі – математикадағы сияты информатикада да басты негіз. Бірақ егер математикада сандарды өңдеу әдістеріне көп көңіл бөлінетін болса, онда информатика үшін сандарды ұсыну әдістерін айналып өтуге болмайды, өйткені тек солар ғана жадтың қажетті қорын, жылдамдықты және есептеуде жіберетін қатені анықтайды.

3 слайд

4 слайд

4 слайд

5 слайд
Позициялық емес санау жүйесінде әрбір цифрдің мәні оның алатын орнына байланысты емес Позияциялық санау жүйесінде цифрдың мәні оның орнына байланысты болады.

5 слайд

6 слайд
• Позициялық емес санау жүйесінде әрбір цифрдің мәні оның алатын орнына байланысты емес деген болатынбыз. Мұндай санау жүйесінің мысалы ретінде римдік жүйені алуға болады. • Римдік санау жүйесінде сандардың орнына латын әріптері қолданылады: I V X L C MD 1 5 10 50 100 500 1000 • Римдік санау жүйесінде 32 саны былай жазылады: XXXII = (X+X+X)+(I+I)= 30+2 • 444 саны римдік жүйеде былай жазылады: CDXLIV=(D-C)+(L-X)+(V-I)= 400+40+4 . • 1974 римдік жүйеде жазылуы: MCMLXXIV= M+(M-C)+L+(X+X)+(V-I)=1000+900+50+20+4 .

6 слайд

7 слайд
Позияциялық санау жүйесінде цифрдың мәні оның орнына байланысты болады. Позициялық санау жүйесінің негізі деп қолданылатын цифрлар санын айтады. Мысалы, 737,7 санындағы бірінші тұрған 7 жүздікті, екіншісі – 7 бірлікті, ал үшіншісі – бірліктің 7 ондық үлесін білдіреді. Кез келген позициялық санау жүйесі өзінің негізімен сипатталады.

7 слайд

8 слайд
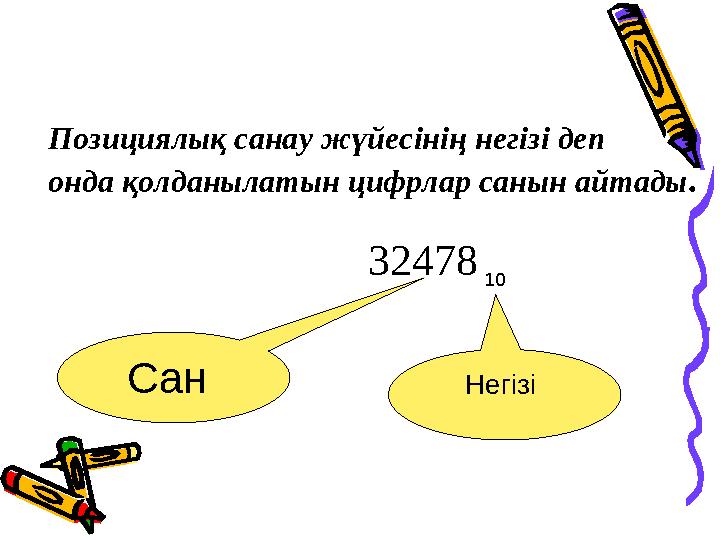
Сан Негізі 32478 10Позициялық санау жүйесінің негізі деп онда қолданылатын цифрлар санын айтады .

8 слайд

9 слайд
 . ... ... 2 2 1 1 0 0 2 2 1 1 m m n n n n q q a q a q a q a q a q a A                    10 . 10 8 10 7 10 4 10 2 10 3 8 10 7 100 4 1000 2 10000 3 0 1 2 3 4                   32478 = бірлік ондық жүздік мыңдық Мұндағы А – сан, q – санау жүйесінің негізі, а – санау жүйесінің цифрлары, n мен m – сәйкес бүтін және бөлшек разрядтардың саны. Мысалы:

9 слайд

10 слайд
Санау жүйесі Негізі Алфавиттегі өлшемі саны Екілік 2 2 0, 1 Сегіздік 8 8 0,1,2,3,4,5,6,7 Ондық 10 10 0,1,2,3,4,5,6,7,8,9 Он алтылық 16 16 0,1,2,3,4,5,6,7,8,9, А,В,С, D , T , F

10 слайд

11 слайд
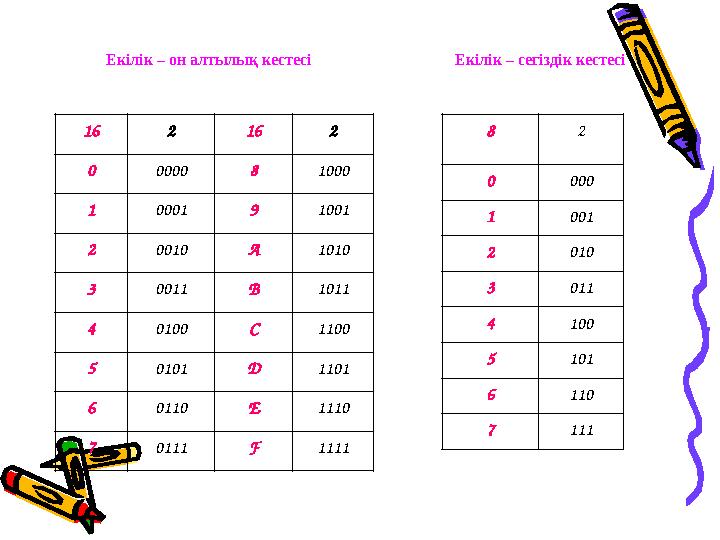
16 2 16 2 0 0000 8 1000 1 0001 9 1001 2 0010 А 1010 3 0011 В 1011 4 0100 С 1100 5 0101 D 1101 6 0110 Е 1110 7 0111 F 1111 8 2 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111Екілік – он алтылық кестесі Екілік – сегіздік кестесі

11 слайд

12 слайд
Ауыстыру ережесі Бүтін оң ондық санды екілік санау жүйесіне ауыстыру үшін осы санды 2-ге бөлу керек. Алынған бөліндіні қайтадан екіге бөліп және т.с.с.., алынған бөлінді 2-ден кіші болғанша бөле беру керек. Нәтижесінде соңғы бөлінді мен соңғысынан бастап барлық қалдықтарды бір жолға жазу керек. Ондық оң бөлшекті екілік санау жүйесіне ауыстыру үшін бөлшекті 2-ге көбейту керек.Көбейтіндінің бүтін бөлігін екілік бөлшектің үтірден кейінгі бірінші цифры ретінде алып, бөлшек бөлігін қайтадан 2-ге көбейту керек. Енді бұл көбейтіндінің бүтін бөлігін екілік бөлшектің келесі цифры ретінде алып, бөлшек бөлігін тағы 2-ге көбейту керек және т.с.с.

12 слайд

13 слайд
315 24 75 72 3 8 32 7 8 4 315 16 916 155 144 11 (В) 16 3 16 115 2 2 214 1 7 6 1 3 2 1 1Екілік Сегіздік Он алтылық2 10 1111 15  8 10 473 315  39 1 1610 13В315 

13 слайд

14 слайд
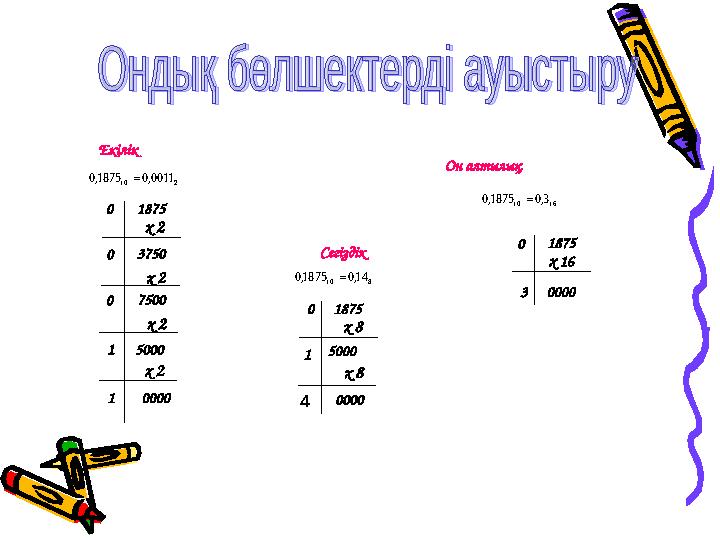
3750 5000 00000 1 х 20 1875 7500 10 х 2х 2 х 2 0 1875 0000 х 16 3 0 1875 00001 х 8х 8 4 5000Екілік Сегіздік Он алтылық 2 10 0011,0 1875,0  8 10 14,0 1875,0  16 10 3,0 1875,0 

14 слайд

15 слайд
Қосу кестесі 0+0=0 1+0=1 0+1=1 1+1=10 Алу кестесі 0-0=0 1-0=1 1-1=0 10-1=1 Көбейту кестесі 0*0=0 1*0=0 1*1=1 1 1 0 1 1 1 0 1 1 0 1 1 0 0 1 0 0 0 + 1 0 0 1 0 0 0 1 0 1 1 0 1 1 1 0 1 1_ 1 1 0 0 1 1 0 0 0 1* 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 + 1 1 0 1 0 1 0 0 1

15 слайд