Материалдар / Шеңбер бойымен қисық сызықты қозғалыс

Шеңбер бойымен қисық сызықты қозғалыс

Материал туралы қысқаша түсінік

Физика пәнінен тақырыпты түсіндіргенде көмекші құрал

Тоқсанбаева Айнұр Амангелдіқызы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

02 Наурыз 2019

1034

0 рет жүктелген

Физика Презентация 9 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 11

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд
• Дененің қисық траектория бойымен қозғалысын қисық сызықты қозғалысы деп атайды. • Қозғалыс траекториясы:

2 слайд

• Дененің қисық траектория бойымен қозғалысын қисық сызықты қозғалысы деп атайды. • Қозғалыс траекториясы:

3 слайд
Шеңбер бойымен

3 слайд

Шеңбер бойымен

4 слайд
 Сызықтық жылдамдық, v (м / с).  Бұрыштық жылдамдық,  (рад / с).  Центрге тартқыш үдеу, а n (м / с ² ).  Тангенциал үдеу , а t (м / с ² ).  Айналу периоды, Т (с).  Айналу жиілігі,  (рад / с).

4 слайд

 Сызықтық жылдамдық, v (м / с).  Бұрыштық жылдамдық,  (рад / с).  Центрге тартқыш үдеу, а n (м / с ² ).  Тангенциал үдеу , а t (м / с ² ).  Айналу периоды, Т (с).  Айналу жиілігі,  (рад / с).

5 слайд
Егер дене шеңбер бойымен бірқалыпты жылдамдықпен айналатын болса, онда бұл қозғалыс бірқалыпты шеңбер бойымен қозғалыс деп аталады.

5 слайд

Егер дене шеңбер бойымен бірқалыпты жылдамдықпен айналатын болса, онда бұл қозғалыс бірқалыпты шеңбер бойымен қозғалыс деп аталады.

6 слайд
, d υ d υ lim a 0 t t t         Шеңберді айналу барысында дененің жылдамдық векторының бағыты тұрақты өзгеріп отырады, яғни үдеуді тудырады. Сол үдеуді қарастырайық: • Ондағы -  t уақыт ішіндегі жылдамдықтың өзгерісі . Бұл жағдайда бізді уақыттың өте аз мәніндегі, лездік жылдамдықты қарастырамыз. • Анықталған үдеү центрге тартқыш үдеу ( нормаль үдеу )деп аталады. υ  

6 слайд

, d υ d υ lim a 0 t t t         Шеңберді айналу барысында дененің жылдамдық векторының бағыты тұрақты өзгеріп отырады, яғни үдеуді тудырады. Сол үдеуді қарастырайық: • Ондағы -  t уақыт ішіндегі жылдамдықтың өзгерісі . Бұл жағдайда бізді уақыттың өте аз мәніндегі, лездік жылдамдықты қарастырамыз. • Анықталған үдеү центрге тартқыш үдеу ( нормаль үдеу )деп аталады. υ  

7 слайд
Біз күнделікті өмірде бірқалыпты шеңбер бойымен қозғалысты жиі кездестіреміз.

7 слайд

Біз күнделікті өмірде бірқалыпты шеңбер бойымен қозғалысты жиі кездестіреміз.

8 слайд
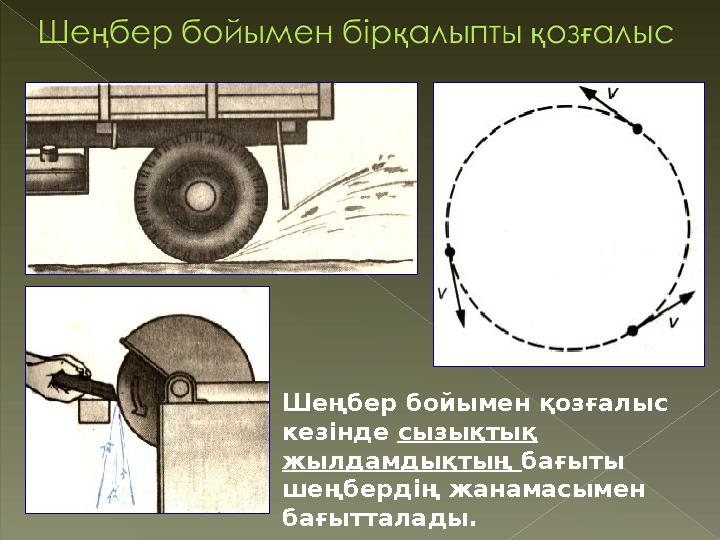
Шеңбер бойымен қозғалыс кезінде сызықтық жылдамдықтың бағыты шеңбердің жанамасымен бағытталады.

8 слайд

Шеңбер бойымен қозғалыс кезінде сызықтық жылдамдықтың бағыты шеңбердің жанамасымен бағытталады.

9 слайд
Егер дене шеңбер бойымен қозғалыс барысында жылдадығының мәні өзгеріп отыратын болса, бұл қозғалыс шеңбер бойымен теңайнымалы қозғалыс деп аталады. a 

9 слайд

Егер дене шеңбер бойымен қозғалыс барысында жылдадығының мәні өзгеріп отыратын болса, бұл қозғалыс шеңбер бойымен теңайнымалы қозғалыс деп аталады. a 

10 слайд
= + . a  a  n a  Шеңбер бойымен теңайнымалы қозғалыс барысында центрге тартқыш, , үдеуден басқа тангенциалды, , үдеу орын алады. Толық үдеу нормаль (центрге тартқыш) және тангенциал үдеулердің векторлық қосындысына тең.  Толық үдеудің модульдік мәні тең n a   a  2 2  a a a n  

10 слайд

= + . a  a  n a  Шеңбер бойымен теңайнымалы қозғалыс барысында центрге тартқыш, , үдеуден басқа тангенциалды, , үдеу орын алады. Толық үдеу нормаль (центрге тартқыш) және тангенциал үдеулердің векторлық қосындысына тең.  Толық үдеудің модульдік мәні тең n a   a  2 2  a a a n  