#1 слайд
Right triangle trigonometry KS4 Mathematics

1 слайд

#2 слайд
2 Ширату жаттығуы: «Допты лақтыру» әдісі арқылы өткен тақырыптағы білімдерін сұрақ қойып, еске түсіру арқылы ақпараттардың қажеттіліктерін анықтау. Мақсаты: Өткен сабақты қайталап, кері байланыс алу, қандай да болмасын ақпарат (мәлімет, сұрақ) туралы бар білгендерін ортаға салу. 1. What is the sine of a rectangular triangle? 2. What is the tangent of a rectangular triangle? 3. Can you say the Pythagoras theorem formulas 4. What triangle is a rectangular triangle? 5. Name the elements of a rectangular triangle.

2 слайд

#3 слайд
3 The four trigonometric functions of a right triangle, with an acute angle α, are defined by ratios of two sides of the triangle. The sides of the right triangle are:  the side opposite the acute angle α,  the side adjacent to the acute angle α,  and the hypotenuse of the right triangle. The trigonometric functions are sine, cosine, tangent, cotangent. opp adj hyp α sin α = cos α = tan α = cot α = hyp adj adj opp opp adj hyp opp

3 слайд

#4 слайд
Video

4 слайд

#5 слайд
New lesson Жаңа сабақ

5 слайд

#6 слайд
Оқу мақсаты: • 8.1.3.6 тікбұрышты үшбұрышты 30°, 45°, 60°-қа тең бұрыштардың синус, косинус, тангенс және котангенсінің мәндерін табу үшін қолдану. •Сабақ мақсаты: • Оқушылардың барлығы: 30 0 , 45 0 , 60 0 бұрыштарының синусы, косинусы, тангенсі, котангенсі мәндерін табуды қолданады • Оқушылардың басым бөлігі: 30 0 , 45 0 , 60 0 бұрыштарының синусы, косинусы, тангенсі, котангенсі мәндерін тұжырымдайды • Оқушылардың кейбіреуі:Тікбұрышты үшбұрыштың қабырғаларының қатынасын есеп шығару барысында меңгереді

6 слайд

#7 слайд
A A A A A A S3.4 Sin, cos and tan of any angle S4 Further trigonometry Contents S3.7 Exercises for trigonometric functions S3.7 Conclusion S3.6 Approximately value of trigonometric functions S3.7 Home work

7 слайд

#8 слайд
8 Suppose we have an equilateral triangle of side length 2. We can use this triangle to write exact values for sin, cos and tan 30°: sin 30° = 1 2 cos 30° = 3 2 tan 30° = 2 2 2 60° 60° 60° 2 60° 30° 1 If we cut the triangle in half then we have a right-angled triangle with acute angles of 30° and 60°. Using Pythagoras’ theorem, = 3 3 The height of the triangle =  2² – 1² 3 3 Sin, cos and tan of 30°

8 слайд

#9 слайд
Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 9 45° 45° 1 1 Using Pythagoras’ theorem, = 2 2 We can use this triangle to write exact values for sin, cos and tan 45°: sin 45° = 2 2 cos 45° = tan 45° =1 The hypotenuse =  1² + 1² 2 2

9 слайд

#10 слайд
Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 10 Example 2 60° 30° 1 If we cut the triangle in half then we have a right-angled triangle with acute angles of 30° and 60°. = 3 3 The height of the triangle =  2² – 1² We can also use this triangle to write exact values for sin, cos and tan 60°: sin 60° = cos 60° = 3 2 tan 60° = 1 2 3

10 слайд

#11 слайд
Trigonometry (SOHCAHTOA) MATHSWATCH CLIP 168, 173, 218 GRADE 5, 8/9 Exact values of trig functions 21.10.23 The exact values of the sine, cosine and tangent of 30°, 45° and 60° can be summarized as follows: 30° sin cos tan 45° 60° 1 2 2 2 1 2 3 2 1 3 2 1 2 3 3 3

11 слайд

#12 слайд
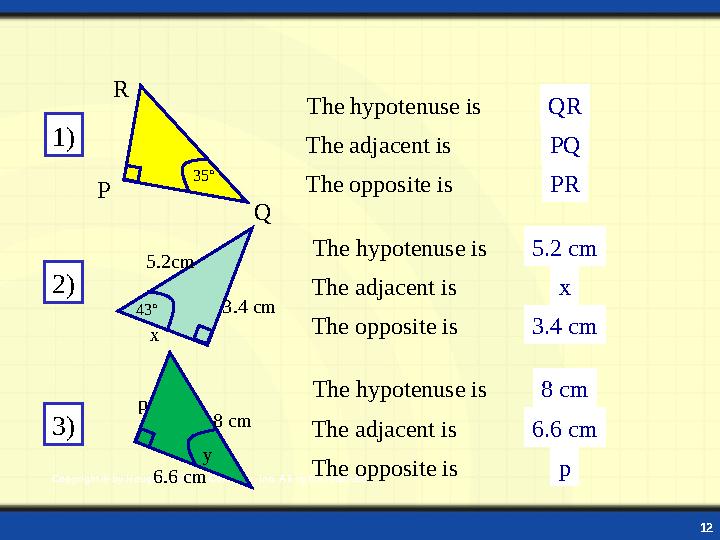
Copyright © by Houghton Mifflin Company, Inc. All rights reserved. 12 The hypotenuse is The adjacent is The opposite is The hypotenuse is The adjacent is The opposite is The hypotenuse is The adjacent is The opposite is 1) 2) 3) P Q R 35° QR PQ PR 43° 5.2cm x 3.4 cm 5.2 cm x 3.4 cm y 8 cm p 6.6 cm 8 cm 6.6 cm p

12 слайд

#13 слайд
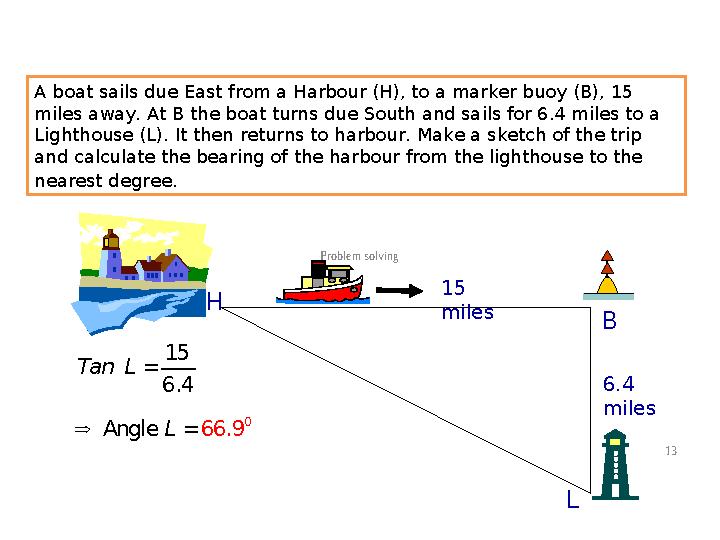
13 Problem solving A boat sails due East from a Harbour (H), to a marker buoy (B), 15 miles away. At B the boat turns due South and sails for 6.4 miles to a Lighthouse (L). It then returns to harbour. Make a sketch of the trip and calculate the bearing of the harbour from the lighthouse to the nearest degree.  15 6.4 Tan L H B L 15 miles 6.4 miles   0 Angle 66.9L

13 слайд

#14 слайд

14 слайд

#15 слайд
Exercise:  A ship travels 10 km on a course heading 50º east of north. How far north has the ship travelled at this point? Exercise:  A ship travels 10 km on a course heading 50º east of north. How far north has the ship travelled at this point?

15 слайд

#16 слайд

16 слайд