Материалдар / Стереометрия аксиомалары және олардың салдарлары

Стереометрия аксиомалары және олардың салдарлары

Материал туралы қысқаша түсінік

Маралбекова Шырайлы Арыновна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

07 Сәуір 2023

1001

6 рет жүктелген

Директорға Сабақ жоспары 11 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 38

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
«Прогресс» политехникалық колледж математика пәнінің оқытушысы Маралбекова Ш.А. Өтеген батыр ауылы

1 слайд

«Прогресс» политехникалық колледж математика пәнінің оқытушысы Маралбекова Ш.А. Өтеген батыр ауылы

2 слайд
Сабақтың мақсаты: - Стереометрия аксиомалары мен олардың салдарларын білу; - Стереометрияның аксиомаларын сызбада бейнелеп, математикалық символдармен жазу; - Аксиомалардан шығатын кейбір қарапайым салдарды дәлелдеп, оларды есептер шығаруда қолдану

2 слайд

Сабақтың мақсаты: - Стереометрия аксиомалары мен олардың салдарларын білу; - Стереометрияның аксиомаларын сызбада бейнелеп, математикалық символдармен жазу; - Аксиомалардан шығатын кейбір қарапайым салдарды дәлелдеп, оларды есептер шығаруда қолдану

3 слайд
К үтілетін нәтижелер Бағалау критерийлері: Оқушы төмендегі критерийлерді орындаса, оқу мақсатына жетеді - стереометрияның аксиомаларын сызбада кескіндейді және математикалық символдарды қолданып дұрыс жазады; - аксиомалардан шығатын кейбір қарапайым салдарларды дәлелдеп, оларды есептер шығаруда қолданады; - стереометрия аксиомалары мен олардың салдарларын тұжырымдайды; - аксиомаларға сүйеніп теоремаларды дәледейді, жауаптарын негіздейді.

3 слайд

К үтілетін нәтижелер Бағалау критерийлері: Оқушы төмендегі критерийлерді орындаса, оқу мақсатына жетеді - стереометрияның аксиомаларын сызбада кескіндейді және математикалық символдарды қолданып дұрыс жазады; - аксиомалардан шығатын кейбір қарапайым салдарларды дәлелдеп, оларды есептер шығаруда қолданады; - стереометрия аксиомалары мен олардың салдарларын тұжырымдайды; - аксиомаларға сүйеніп теоремаларды дәледейді, жауаптарын негіздейді.

4 слайд
Қайталау үшін сұрақтар: 1. Төртбұрыштың түрлерін ата 2. Үшбұрыштың, трапецияның орта сызығының қандай қасиеттерін білесің? 3. Дөңгелектің ауданы, шеңбердің ұзындығы қандай формуламен анықталады?

4 слайд

Қайталау үшін сұрақтар: 1. Төртбұрыштың түрлерін ата 2. Үшбұрыштың, трапецияның орта сызығының қандай қасиеттерін білесің? 3. Дөңгелектің ауданы, шеңбердің ұзындығы қандай формуламен анықталады?

5 слайд
Мектептегі геометрия курсы екі бөлімнен тұрады: • ПЛАНИМЕТРИЯ Планиметрия- жазықтықтағы геометриялық фигураларды қарастыратын геометрияның тармағы. • СТЕРЕОМЕТРИЯ Кеңістіктегі фигураларды қарастыратын геометрия тармағы. «Стереометрия» сөзі грек тілінен аударғанда «стерео» - кеңістік және «метрия» - өлшеу дегенді білдіреді.

5 слайд

Мектептегі геометрия курсы екі бөлімнен тұрады: • ПЛАНИМЕТРИЯ Планиметрия- жазықтықтағы геометриялық фигураларды қарастыратын геометрияның тармағы. • СТЕРЕОМЕТРИЯ Кеңістіктегі фигураларды қарастыратын геометрия тармағы. «Стереометрия» сөзі грек тілінен аударғанда «стерео» - кеңістік және «метрия» - өлшеу дегенді білдіреді.

6 слайд
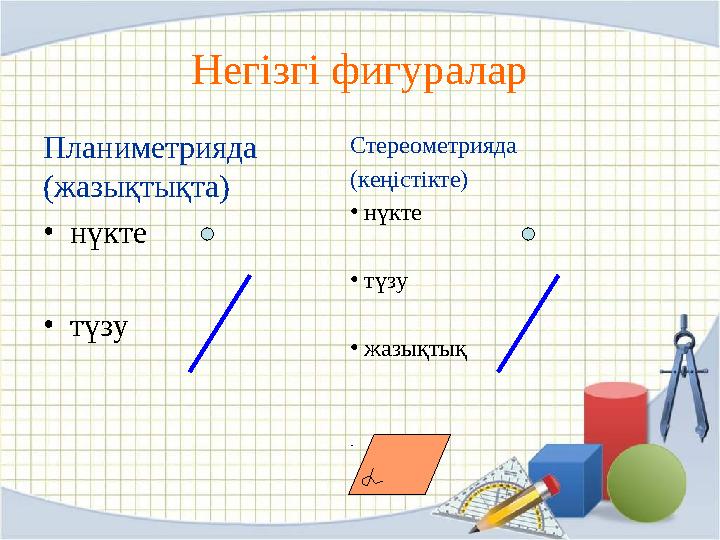
Негізгі фигуралар Планиметрияда (жазықтықта) • нүкте • түзу Стереометрияда (кеңістікте) • нүкте • түзу • жазықтық .

6 слайд

Негізгі фигуралар Планиметрияда (жазықтықта) • нүкте • түзу Стереометрияда (кеңістікте) • нүкте • түзу • жазықтық .

7 слайд
7Стереометрияда нүкте, түзу, жазықтықпен қатар геометриялық денелер , оның қасиеттері қарастырылады, аудандары мен көлемдері есептелінеді. шар куб цилиндр

7 слайд

7Стереометрияда нүкте, түзу, жазықтықпен қатар геометриялық денелер , оның қасиеттері қарастырылады, аудандары мен көлемдері есептелінеді. шар куб цилиндр

8 слайд
8А В С Е a b d α βγНүктелер латынның бас әріптерімен белгіленеді А, В, С, D , Е, К,… Түзулер латыннның кіші әріптерімен белгіленеді a, b, c, d, e, k,… Жазықтақтар грек әріптерімен белгіленеді α , β , γ , λ , π , ω ,…

8 слайд

8А В С Е a b d α βγНүктелер латынның бас әріптерімен белгіленеді А, В, С, D , Е, К,… Түзулер латыннның кіші әріптерімен белгіленеді a, b, c, d, e, k,… Жазықтақтар грек әріптерімен белгіленеді α , β , γ , λ , π , ω ,…

9 слайд
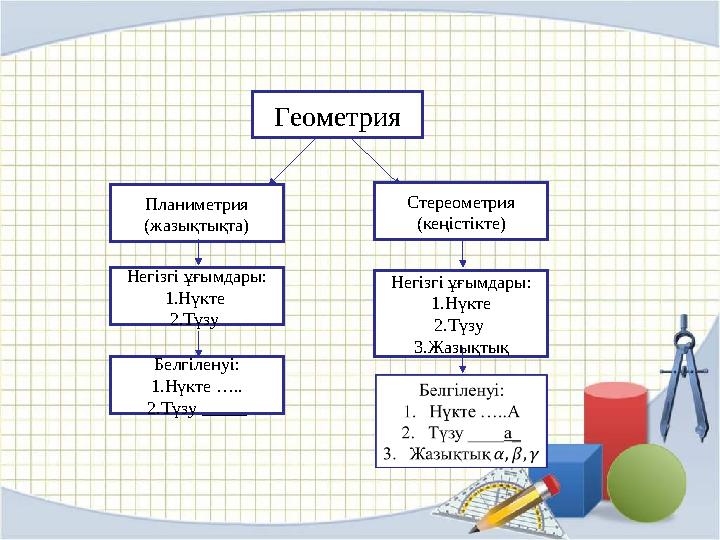
Геометрия Планиметрия (жазықтықта) Стереометрия (кеңістікте) Негізгі ұғымдары: 1. Нүкте 2. Түзу Негізгі ұғымдары: 1. Нүкте 2. Түзу 3. Жазықтық Белгіленуі: 1. Нүкте ….. 2. Түзу _____

9 слайд

Геометрия Планиметрия (жазықтықта) Стереометрия (кеңістікте) Негізгі ұғымдары: 1. Нүкте 2. Түзу Негізгі ұғымдары: 1. Нүкте 2. Түзу 3. Жазықтық Белгіленуі: 1. Нүкте ….. 2. Түзу _____

10 слайд
10Стереометрия құрылыста кеңінен қолданыладыГеометриялық фигуралардың – қиялдағы заттардың қасиеттерін зерттей отырып, біз нақты заттардың геометриялық қасиеттері (олардың пішіні, салыстырмалы орналасуы және т.б.) туралы түсінік аламыз және бұл қасиеттерді тәжірибеде пайдалана аламыз. Бұл геометрияның қолданбалы мәні.

10 слайд

10Стереометрия құрылыста кеңінен қолданыладыГеометриялық фигуралардың – қиялдағы заттардың қасиеттерін зерттей отырып, біз нақты заттардың геометриялық қасиеттері (олардың пішіні, салыстырмалы орналасуы және т.б.) туралы түсінік аламыз және бұл қасиеттерді тәжірибеде пайдалана аламыз. Бұл геометрияның қолданбалы мәні.

11 слайд
11Архитектурада

11 слайд

11Архитектурада

12 слайд
12Машина жасауда

12 слайд

12Машина жасауда

13 слайд
13Геодезияда Ғылым мен техниканың басқа да салаларында. Геодезия – Жердің көлемін ж ә не құрамын зерттейтін ғылым.

13 слайд

13Геодезияда Ғылым мен техниканың басқа да салаларында. Геодезия – Жердің көлемін ж ә не құрамын зерттейтін ғылым.

14 слайд
Планеметриядағы сияқты кеңістікте де нүктелердің, түзулердің және жазықтықтардың кейбір қасиеттері дәлелдеусіз қабылданады және аксиомалар деп аталады. Аксиома грек сөзі, ол – қарастырылатын теорияда дәлелдеусіз алынған шындық дегенді білдіреді.

14 слайд

Планеметриядағы сияқты кеңістікте де нүктелердің, түзулердің және жазықтықтардың кейбір қасиеттері дәлелдеусіз қабылданады және аксиомалар деп аталады. Аксиома грек сөзі, ол – қарастырылатын теорияда дәлелдеусіз алынған шындық дегенді білдіреді.

15 слайд
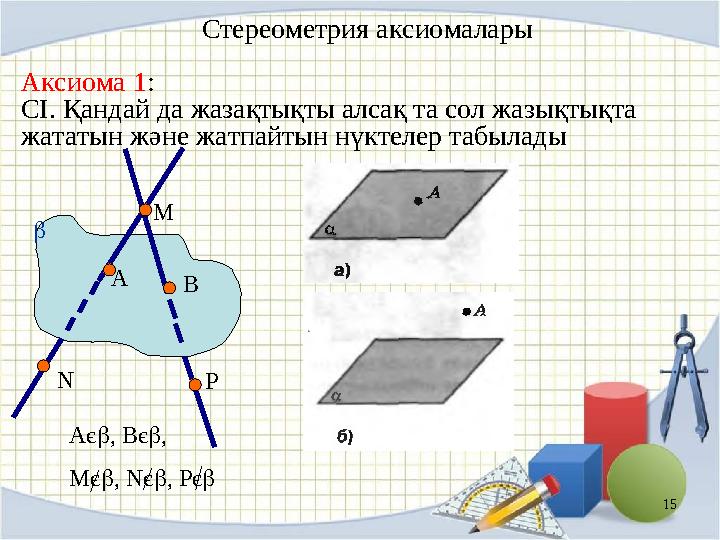
15 Стереометрия аксиомалары Аксиома 1 : СІ. Қандай да жазақтықты алсақ та сол жазықтықта жататын және жатпайтын нүктелер табылады P A є  , B є  , M є  , N є  , P є М А N B

15 слайд

15 Стереометрия аксиомалары Аксиома 1 : СІ. Қандай да жазақтықты алсақ та сол жазықтықта жататын және жатпайтын нүктелер табылады P A є  , B є  , M є  , N є  , P є М А N B

16 слайд
 a a     Күнделікті өмірдегі A 2 аксиомасының ең қарапайым мысалы- бөлменің іргелес екі қабырғасын кесіп өту. Аксиома 2 СІІ. Егер әр түрлі екі жазықтықтың ортақ нүктесі бар болса, онда жазықтықтар осы нүкте арқылы өтетін түзу бойымен қиылысады

16 слайд

 a a     Күнделікті өмірдегі A 2 аксиомасының ең қарапайым мысалы- бөлменің іргелес екі қабырғасын кесіп өту. Аксиома 2 СІІ. Егер әр түрлі екі жазықтықтың ортақ нүктесі бар болса, онда жазықтықтар осы нүкте арқылы өтетін түзу бойымен қиылысады

17 слайд
Аксиома 3 : СІІІ. Егер әр түрлі екі түзудің ортақ нүктесі бар болса, онда бұл екі түзу арқылы жазықтық жүргізуге болады және ол жалғыз ғана болады.

17 слайд

Аксиома 3 : СІІІ. Егер әр түрлі екі түзудің ортақ нүктесі бар болса, онда бұл екі түзу арқылы жазықтық жүргізуге болады және ол жалғыз ғана болады.

18 слайд
18Аксиомалардың салдары Түзу және осы түзуге жатпайтын бір нүкте арқылы бір ғана жазықтық жүргізуге болады. P а Q M α Берілгені : а түзуі, М є α , Дәлелдеу керек : Мє α , ає α , Дәлелдеуі : 1 ) Рє а және Q є а деген екі нүкте алайық 2) Екінші аксиома бойынша бір түзуде жатпыйтын 3 нүкте арқылы бір ғана жазықтық жүргізуге болады 3)Р є α және Q є α нүктелері бір түзуде жатқаннан кейін , аксиома 3 бойынша а є α , олай болса Мє α , ає α . 4) Аксиома 2 ден бір ғана жазықтық бар болғаны шығады. Теорема дәлелденді. Теорема 1

18 слайд

18Аксиомалардың салдары Түзу және осы түзуге жатпайтын бір нүкте арқылы бір ғана жазықтық жүргізуге болады. P а Q M α Берілгені : а түзуі, М є α , Дәлелдеу керек : Мє α , ає α , Дәлелдеуі : 1 ) Рє а және Q є а деген екі нүкте алайық 2) Екінші аксиома бойынша бір түзуде жатпыйтын 3 нүкте арқылы бір ғана жазықтық жүргізуге болады 3)Р є α және Q є α нүктелері бір түзуде жатқаннан кейін , аксиома 3 бойынша а є α , олай болса Мє α , ає α . 4) Аксиома 2 ден бір ғана жазықтық бар болғаны шығады. Теорема дәлелденді. Теорема 1

19 слайд
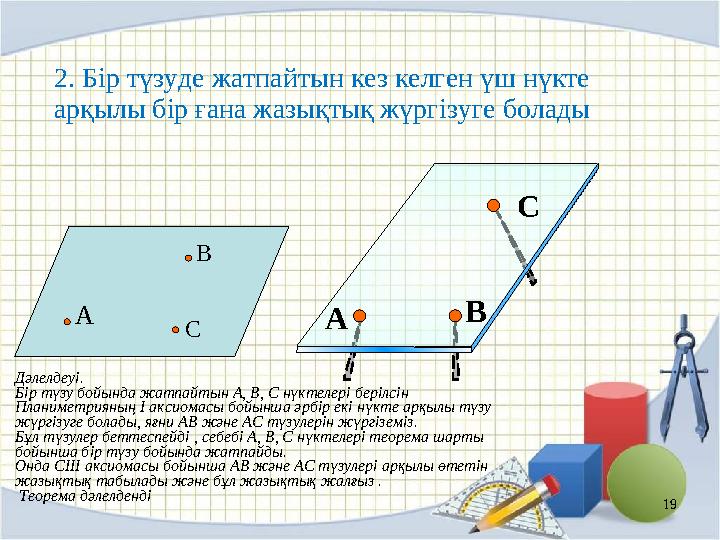
19B A C2. Бір түзуде жатпайтын кез келген үш нүкте арқылы бір ғана жазықтық жүргізуге болады А В С Дәлелдеуі. Бір түзу бойында жатпайтын А, В, С нүктелері берілсін Планиметрияның І аксиомасы бойынша әрбір екі нүкте арқылы түзу жүргізуге болады, яғни АВ және АС түзулерін жүргіземіз. Бұл түзулер беттеспейді , себебі А, В, С нүктелері теорема шарты бойынша бір түзу бойында жатпайды. Онда СІІІ аксиомасы бойынша АВ және АС түзулері арқылы өтетін жазықтық табылады және бұл жазықтық жалғыз . Теорема дәлелденді

19 слайд

19B A C2. Бір түзуде жатпайтын кез келген үш нүкте арқылы бір ғана жазықтық жүргізуге болады А В С Дәлелдеуі. Бір түзу бойында жатпайтын А, В, С нүктелері берілсін Планиметрияның І аксиомасы бойынша әрбір екі нүкте арқылы түзу жүргізуге болады, яғни АВ және АС түзулерін жүргіземіз. Бұл түзулер беттеспейді , себебі А, В, С нүктелері теорема шарты бойынша бір түзу бойында жатпайды. Онда СІІІ аксиомасы бойынша АВ және АС түзулері арқылы өтетін жазықтық табылады және бұл жазықтық жалғыз . Теорема дәлелденді

20 слайд
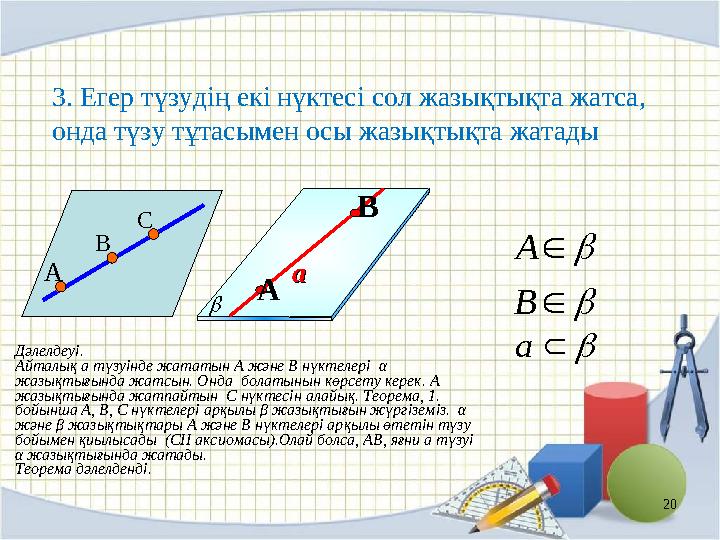
20aa A B     В А  аА В С3. Егер түзудің екі нүктесі сол жазықтықта жатса, онда түзу тұтасымен осы жазықтықта жатады Дәлелдеуі. Айталық а түзуінде жататын А және В нүктелері α жазықтығында жатсын. Онда болатынын көрсету керек. Α жазықтығында жатпайтын С нүктесін алайық. Теорема, 1. бойынша А, В, С нүктелері арқылы β жазықтығын жүргіземіз. α және β жазықтықтары А және В нүктелері арқылы өтетін түзу бойымен қиылысады (СІІ аксиомасы).Олай болса, АВ, яғни а түзуі α жазықтығында жатады. Теорема дәлелденді.

20 слайд

20aa A B     В А  аА В С3. Егер түзудің екі нүктесі сол жазықтықта жатса, онда түзу тұтасымен осы жазықтықта жатады Дәлелдеуі. Айталық а түзуінде жататын А және В нүктелері α жазықтығында жатсын. Онда болатынын көрсету керек. Α жазықтығында жатпайтын С нүктесін алайық. Теорема, 1. бойынша А, В, С нүктелері арқылы β жазықтығын жүргіземіз. α және β жазықтықтары А және В нүктелері арқылы өтетін түзу бойымен қиылысады (СІІ аксиомасы).Олай болса, АВ, яғни а түзуі α жазықтығында жатады. Теорема дәлелденді.

21 слайд
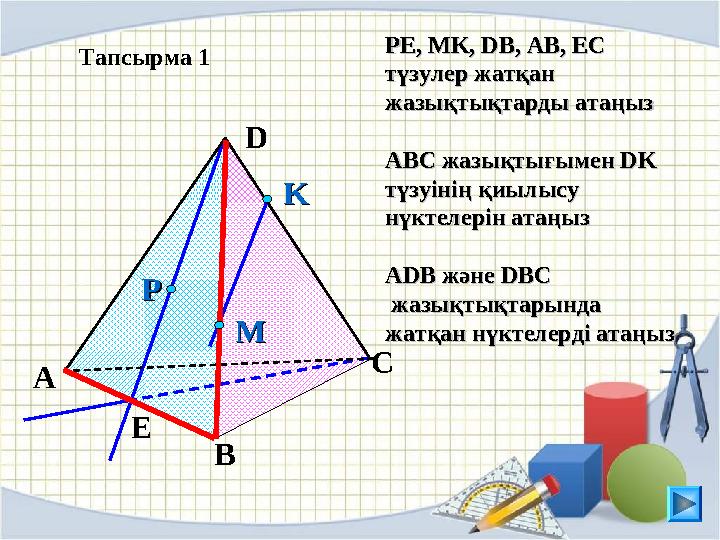
Тапсырма 1 РР E, MK, DB, AB, ECE, MK, DB, AB, EC түзулер жатқан түзулер жатқан жазықтықтарды атаңызжазықтықтарды атаңыз АВС жазықтығымен АВС жазықтығымен DK DK түзуінің қиылысу түзуінің қиылысу нүктелерін атаңызнүктелерін атаңыз АА DB DB және және DBCDBC жазықтықтарында жазықтықтарында жатқан нүктелерді атаңызжатқан нүктелерді атаңызPP EA B CD MM KK

21 слайд

Тапсырма 1 РР E, MK, DB, AB, ECE, MK, DB, AB, EC түзулер жатқан түзулер жатқан жазықтықтарды атаңызжазықтықтарды атаңыз АВС жазықтығымен АВС жазықтығымен DK DK түзуінің қиылысу түзуінің қиылысу нүктелерін атаңызнүктелерін атаңыз АА DB DB және және DBCDBC жазықтықтарында жазықтықтарында жатқан нүктелерді атаңызжатқан нүктелерді атаңызPP EA B CD MM KK

22 слайд
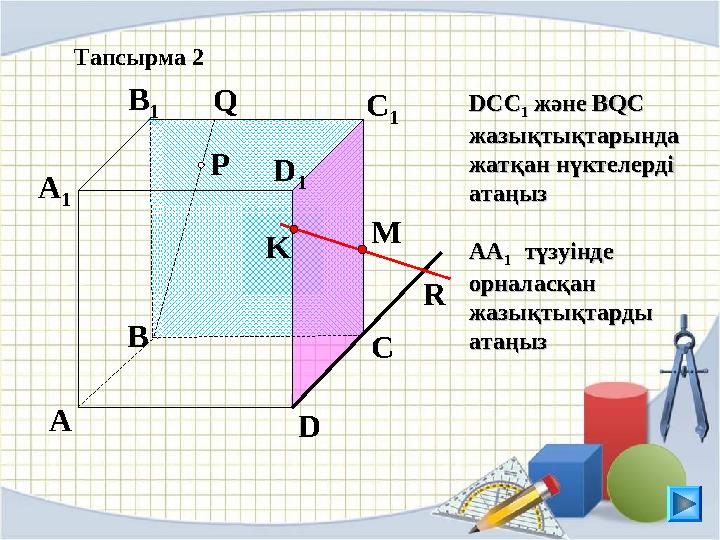
P A B C DA 1 B 1 C 1 D 1 RM KQ Тапсырма 2 DCCDCC 11 және және BQCBQC жазықтықтарында жазықтықтарында жатқан нүктелерді жатқан нүктелерді атаңызатаңыз АААА 1 1 түзуінде түзуінде орналасқан орналасқан жазықтықтарды жазықтықтарды атаңызатаңыз

22 слайд

P A B C DA 1 B 1 C 1 D 1 RM KQ Тапсырма 2 DCCDCC 11 және және BQCBQC жазықтықтарында жазықтықтарында жатқан нүктелерді жатқан нүктелерді атаңызатаңыз АААА 1 1 түзуінде түзуінде орналасқан орналасқан жазықтықтарды жазықтықтарды атаңызатаңыз

23 слайд
Бағалау критерийлері Дескриптор -математикалық символдарды қолданып, дұрыс жазады; А - қажетті математикалық символдарды таңдайды; - сөйлемді символдармен қысқаша дұрыс жазады. - Тапсырманың басым бөлігін дұрыс орындайды. - тапсырманы сызбада кескіндейді ; - аксиомалар мен олардан шығатын салдарларды қолданып есептер шығарады. В - есептің шартына сәйкес сызба салады - жазықтықтың санын анықтайды. - мүмкін жағдайдың бәрін қарастырады - жауаптарын негіздейді - стереометрия аксиомалары мен олардың салдарларын дәлелдеуге қолданады. С - теореманы тұжырымдайды - дұрыс/бұрыстығын анықтайды - аксиомаларға сүйеніп дәлелдейді Жеке жұмыс :

23 слайд

Бағалау критерийлері Дескриптор -математикалық символдарды қолданып, дұрыс жазады; А - қажетті математикалық символдарды таңдайды; - сөйлемді символдармен қысқаша дұрыс жазады. - Тапсырманың басым бөлігін дұрыс орындайды. - тапсырманы сызбада кескіндейді ; - аксиомалар мен олардан шығатын салдарларды қолданып есептер шығарады. В - есептің шартына сәйкес сызба салады - жазықтықтың санын анықтайды. - мүмкін жағдайдың бәрін қарастырады - жауаптарын негіздейді - стереометрия аксиомалары мен олардың салдарларын дәлелдеуге қолданады. С - теореманы тұжырымдайды - дұрыс/бұрыстығын анықтайды - аксиомаларға сүйеніп дәлелдейді Жеке жұмыс :

24 слайд
1.Іздену: Теорема, 1. Бір түзу бойында жатпайтын үш нүкте арқылы бір ғана жазықтық өтеді. Дәлелдеуі. Теорема, 2. Түзу мен оның бойында жатпайтын нүкте арқылы бір ғана жазықтық өтеді. Дәлелдеуі. Теорема, 3. Егер түзудің екі нүктесі берілген жазықтықта жатса, түзу толығымен осы жазықтықта жатады. Дәлелдеуі.

24 слайд

1.Іздену: Теорема, 1. Бір түзу бойында жатпайтын үш нүкте арқылы бір ғана жазықтық өтеді. Дәлелдеуі. Теорема, 2. Түзу мен оның бойында жатпайтын нүкте арқылы бір ғана жазықтық өтеді. Дәлелдеуі. Теорема, 3. Егер түзудің екі нүктесі берілген жазықтықта жатса, түзу толығымен осы жазықтықта жатады. Дәлелдеуі.

25 слайд
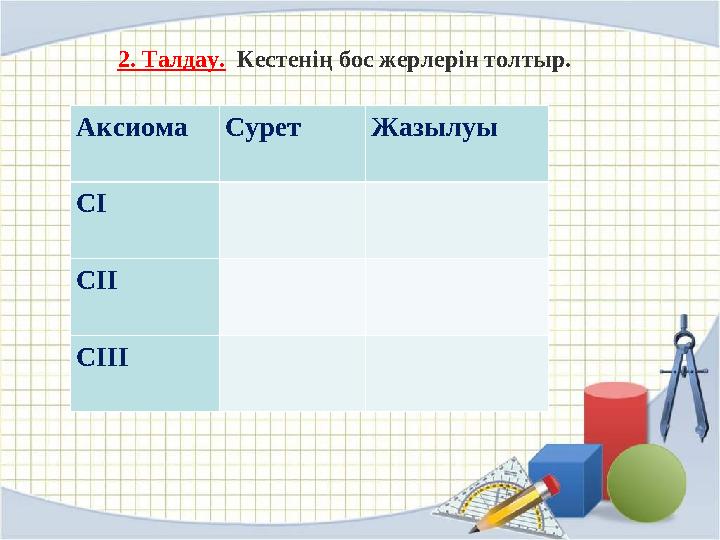
2. Талдау. Кестенің бос жерлерін толтыр. Аксиома Сурет Жазылуы СІ СІІ СІІІ

25 слайд

2. Талдау. Кестенің бос жерлерін толтыр. Аксиома Сурет Жазылуы СІ СІІ СІІІ

26 слайд
3. Салу. № Сөйлемдер Символдарды пайдаланып, математика тілімен жазу Сызба сын салу 1 А нүктесі а түзуінде жатады 2 а түзуі А және В нүктелері арқылы өтеді 3 a және b түзулері О нүктесінде қиылысады 4 α және β жазықтықтары а түзуі бойымен қиылысады 5 α жазықтығы а түзуімен А нүктесі арқылы қиылысады 6 С нүктесі γ жазықтығында жатпайды 7 γ жазықтығы бір түзудің бойында жатпайтын А, В, және нүктелері арқылы өтеді.

26 слайд

3. Салу. № Сөйлемдер Символдарды пайдаланып, математика тілімен жазу Сызба сын салу 1 А нүктесі а түзуінде жатады 2 а түзуі А және В нүктелері арқылы өтеді 3 a және b түзулері О нүктесінде қиылысады 4 α және β жазықтықтары а түзуі бойымен қиылысады 5 α жазықтығы а түзуімен А нүктесі арқылы қиылысады 6 С нүктесі γ жазықтығында жатпайды 7 γ жазықтығы бір түзудің бойында жатпайтын А, В, және нүктелері арқылы өтеді.

27 слайд
4.Тұжырымдау: Математикалық тілмен берілген есептерді дәлелдеп, сөзбен тұжырымдаңдар

27 слайд

4.Тұжырымдау: Математикалық тілмен берілген есептерді дәлелдеп, сөзбен тұжырымдаңдар

28 слайд
«Өзін-өзі бағалау» «Бағдаршам» әдісі арқылы

28 слайд

«Өзін-өзі бағалау» «Бағдаршам» әдісі арқылы

29 слайд
Кеңістіктегі екі нүкте арқылы неше түзу жүргізуге болады? Жауабы: жалғыз.Сабақты бекіту

29 слайд

Кеңістіктегі екі нүкте арқылы неше түзу жүргізуге болады? Жауабы: жалғыз.Сабақты бекіту

30 слайд
Кеңістіктегі үш нүкте арқылы неше жазықтық жүргізуге болады? жауабы: бір, егер үш нүкте бір түзудің бойында жатпаса

30 слайд

Кеңістіктегі үш нүкте арқылы неше жазықтық жүргізуге болады? жауабы: бір, егер үш нүкте бір түзудің бойында жатпаса

31 слайд
Екі жазықтықтың қанша ортақ нүктесі болуы мүмкін? жауабы: ортақ нүктесі жоқ немесе шексіз көп

31 слайд

Екі жазықтықтың қанша ортақ нүктесі болуы мүмкін? жауабы: ортақ нүктесі жоқ немесе шексіз көп

32 слайд
Келесі тұжырымдар дұрыс па? а) кез келген үш нүкте бір жазықтықта жатады б) кез келген төрт нүкте бір жазықтықта жатады жауабы : а) иа; б) жоқ.

32 слайд

Келесі тұжырымдар дұрыс па? а) кез келген үш нүкте бір жазықтықта жатады б) кез келген төрт нүкте бір жазықтықта жатады жауабы : а) иа; б) жоқ.

33 слайд
Тұжырымдама дұрыс па? Егер шеңбер мен жазықтықтың ортақ екі нүктесі болса, онда шеңбер жазықтықта жатады. жауабы : жоқ

33 слайд

Тұжырымдама дұрыс па? Егер шеңбер мен жазықтықтың ортақ екі нүктесі болса, онда шеңбер жазықтықта жатады. жауабы : жоқ

34 слайд
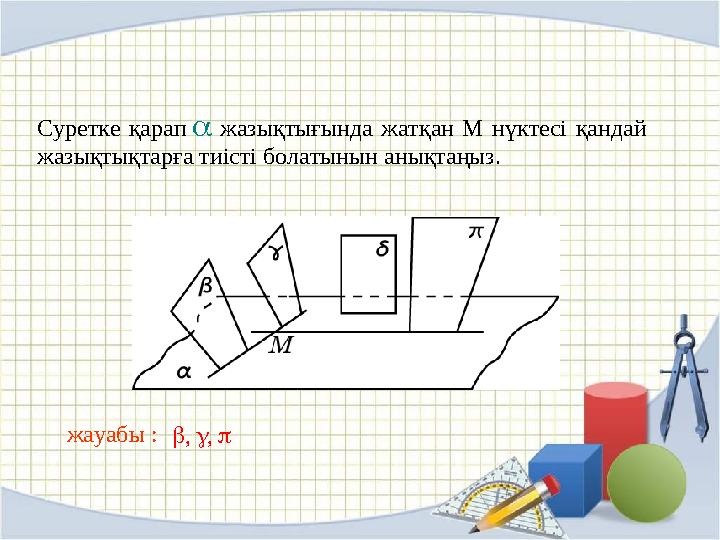
жауабы :, ,   Суретке қарап жазықтығында жатқан М нүктесі қандай жазықтықтарға тиісті болатынын анықтаңыз. 

34 слайд

жауабы :, ,   Суретке қарап жазықтығында жатқан М нүктесі қандай жазықтықтарға тиісті болатынын анықтаңыз. 

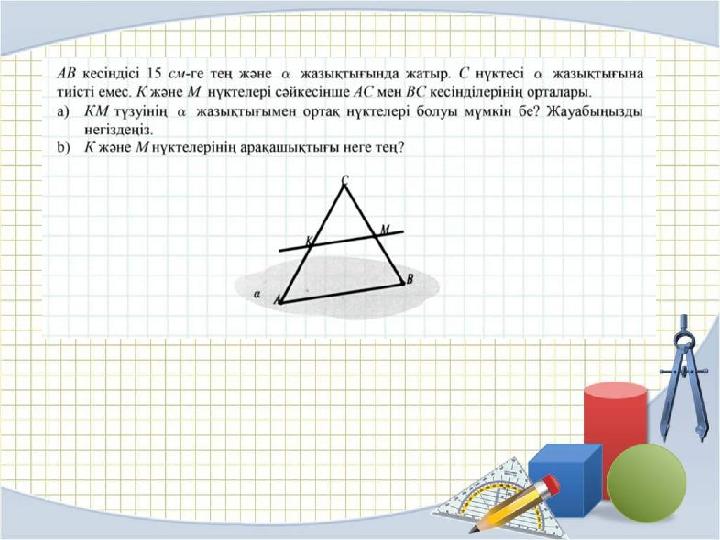
35 слайд

36 слайд

37 слайд