Материалдар / Теңдеулер презентация

Теңдеулер презентация

Материал туралы қысқаша түсінік

Презентация теңдеулер мен теңсіздіктер туралы. Толық баяндалған, түсінікті жасалған. Сабақта қолдана аласыз. Теңдеулерге анықтама берілген және түрлері баяндалған. Теңсіздіктерге анықтама берілген және түрлері баяндалған

Мейірханқызы Гүлжайна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

30 Қырқүйек 2021

779

0 рет жүктелген

Математика Презентация 7 сынып

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 15

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд

3 слайд

4 слайд

5 слайд
Мысалы, a және b параметрлерінің мүмкін мәндерінде функциясы жұп немесе тақ екендігін зерттеу керек. Шешуі: Функцияның анықталу облысы бас нүктеге қарағанда симметриялы болатынын ескереміз. болуы үшін болуы керек. Жауабы: Кез келген мәндерінде функция тақ,

5 слайд

Мысалы, a және b параметрлерінің мүмкін мәндерінде функциясы жұп немесе тақ екендігін зерттеу керек. Шешуі: Функцияның анықталу облысы бас нүктеге қарағанда симметриялы болатынын ескереміз. болуы үшін болуы керек. Жауабы: Кез келген мәндерінде функция тақ,

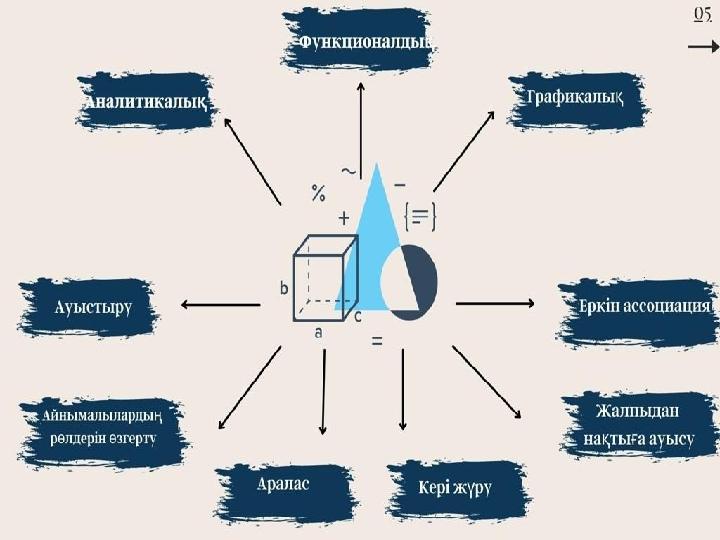
6 слайд

7 слайд
Теңдеуді екі әдіспен шешіңдер: | x + 2| =a. 1 -әдіс . Аналитикалық Анықталу облысы : а  R, x  R. 1. Егер а = 0; | х + 2| = 0, х = - 2. 2. Егер a < 0, | x + 2| = a, ø . 3. Егер a > 0, x + 2 = a және х + 2 = - а, х = а – 2 х = - а - 2. Жауабы: егер a < 0, шешімі жоқ; егер а = 0, онда х = - 2; егер a > 0, онда х 1 = а - 2. х 2 = - а - 2. 2 -әдіс . Графиктік әдіс Координат системасында функция графигін саламыз у = | х + 2| және у = а. у = | х + 2| , Егер , онда немесе , у = а, у = а, - х - 2 = а, х + 2 = а, х = - а – 2 , х = а - 2. Жауабы: егер a < 0 болса шешімі жоқ; егер а = 0, онда х = - 2; егер a > 0, онда х 1 = а - 2. х 2 = - а - 2.

7 слайд

Теңдеуді екі әдіспен шешіңдер: | x + 2| =a. 1 -әдіс . Аналитикалық Анықталу облысы : а  R, x  R. 1. Егер а = 0; | х + 2| = 0, х = - 2. 2. Егер a < 0, | x + 2| = a, ø . 3. Егер a > 0, x + 2 = a және х + 2 = - а, х = а – 2 х = - а - 2. Жауабы: егер a < 0, шешімі жоқ; егер а = 0, онда х = - 2; егер a > 0, онда х 1 = а - 2. х 2 = - а - 2. 2 -әдіс . Графиктік әдіс Координат системасында функция графигін саламыз у = | х + 2| және у = а. у = | х + 2| , Егер , онда немесе , у = а, у = а, - х - 2 = а, х + 2 = а, х = - а – 2 , х = а - 2. Жауабы: егер a < 0 болса шешімі жоқ; егер а = 0, онда х = - 2; егер a > 0, онда х 1 = а - 2. х 2 = - а - 2.

8 слайд
Параметрдің рұқсат етілген мәндерінің ауданы анықталады. Параметрлі теңсіздік бірдей жолмен шешілетін аралықтарға бөлінеді. Теңсіздіктің шешімі олардың әрқайсысы үшін бастапқы теңсіздік тің шешімін көрсете отырып, параметрдің өзгеру аралықтарын санау түрінде жазылады. Әр аралықта параметрге байланысты теңсіздіктің шешімі болады.Параметрі бар теңсіздіктің шешілуі:

8 слайд

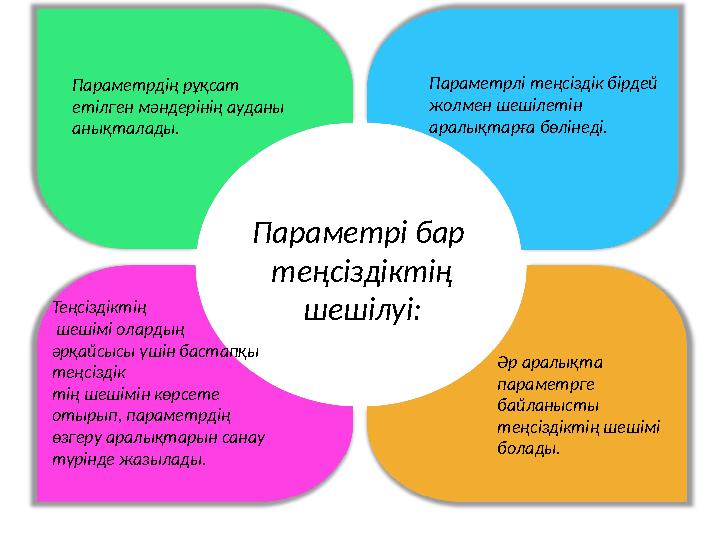
Параметрдің рұқсат етілген мәндерінің ауданы анықталады. Параметрлі теңсіздік бірдей жолмен шешілетін аралықтарға бөлінеді. Теңсіздіктің шешімі олардың әрқайсысы үшін бастапқы теңсіздік тің шешімін көрсете отырып, параметрдің өзгеру аралықтарын санау түрінде жазылады. Әр аралықта параметрге байланысты теңсіздіктің шешімі болады.Параметрі бар теңсіздіктің шешілуі:

9 слайд
Мысал, х-тің барлық мәндерінде теңсіздігін қанағаттандыратын а параметрінің мәндерін табыңыз. а) болғанда, ал екенін ескерсек, болады. б) болғанда ал екенін ескерсек, болады. Жауабы:

9 слайд

Мысал, х-тің барлық мәндерінде теңсіздігін қанағаттандыратын а параметрінің мәндерін табыңыз. а) болғанда, ал екенін ескерсек, болады. б) болғанда ал екенін ескерсек, болады. Жауабы:

10 слайд

11 слайд
Мына теңдеуді Дәстүрлі әдіспен және Maple жүйесіндешешіңіз: а және b параметрлерінің барлық мәндері үшін, , теңдеуді шешіңіз. Шешуі: а) (дәстүрлі әдіспен) Жауабы: б) Maple жүйесінде: > (((x-a)/(b-a))+((x-b)/(a-b))+x=2); > solve(((x-a)/(b-a))+((x-b)/(a-b))+x=2);{ } , ,  a a b b x 1

11 слайд

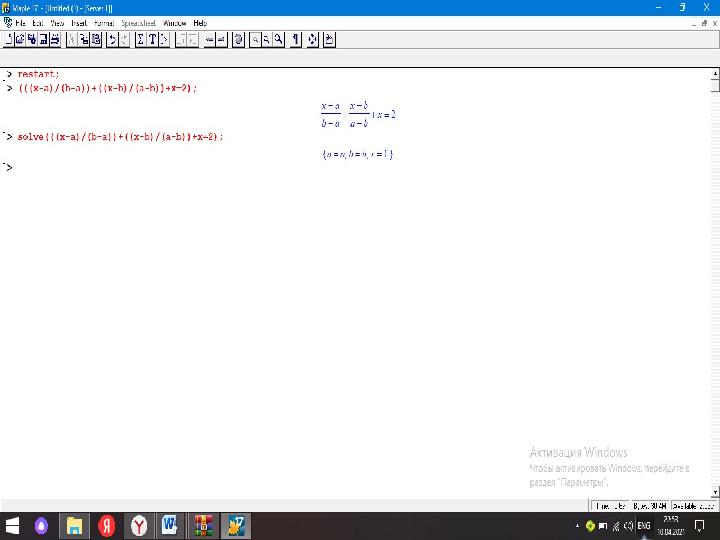
Мына теңдеуді Дәстүрлі әдіспен және Maple жүйесіндешешіңіз: а және b параметрлерінің барлық мәндері үшін, , теңдеуді шешіңіз. Шешуі: а) (дәстүрлі әдіспен) Жауабы: б) Maple жүйесінде: > (((x-a)/(b-a))+((x-b)/(a-b))+x=2); > solve(((x-a)/(b-a))+((x-b)/(a-b))+x=2);{ } , ,  a a b b x 1

12 слайд

13 слайд

14 слайд