Тригонометрические функции и их свойства
Тригонометрические функции и их свойства


#1 слайд
Тема урока:
Тригонометрическ
ие функции и их
свойства.
Цель обучения в соответствии с учебной
программой.
9.2.4.5 находить с помощью единичной окружности
область определения и множество значений
тригонометрических функций
Урок №53
На 20 января Учитель:
Чебакова О.В.
1 слайд
Тема урока: Тригонометрическ ие функции и их свойства. Цель обучения в соответствии с учебной программой. 9.2.4.5 находить с помощью единичной окружности область определения и множество значений тригонометрических функций Урок №53 На 20 января Учитель: Чебакова О.В.

#2 слайд
Актуализация
знаний.
Индивидуальная
работа.
Какая точка получится при повороте точки Р(1; 0) на угол ; ; ; .
При повороте точки Р на угол получается (0; 1).
При повороте точки Р на угол получается (0; - 1).
При повороте точки Р на угол получается (0; - 1).
При повороте точки Р на угол получается ( -1 ; 0 ).
Дескрипторы:
1б записывает координаты точки при повороте на
90 0
1б записывает координаты точки при повороте на
минус 90 0
1б записывает координаты точки при повороте на
270 0
1б записывает координаты точки при повороте на
минус 180 0
2 слайд
Актуализация знаний. Индивидуальная работа. Какая точка получится при повороте точки Р(1; 0) на угол ; ; ; . При повороте точки Р на угол получается (0; 1). При повороте точки Р на угол получается (0; - 1). При повороте точки Р на угол получается (0; - 1). При повороте точки Р на угол получается ( -1 ; 0 ). Дескрипторы: 1б записывает координаты точки при повороте на 90 0 1б записывает координаты точки при повороте на минус 90 0 1б записывает координаты точки при повороте на 270 0 1б записывает координаты точки при повороте на минус 180 0

#3 слайд
Новая тема. Исследование. Работа
в парах.
1. Чему равен косинус углов ?; ;
6 4 3
2. Чему равен синус углов ?
; ;
6 4 3
3. Сделайте вывод.
3 2 1 ; ;
6 3 2 4 4 2 3 6 2
Cos Sin Cos Sin Cos Sin
Дескрипторы:
1б записывает значения косинуса 30 0
и синуса 60 0
1б записывает значения синуса и косинуса 45 0
1б записывает значения косинуса 600 и синуса 30 0
1б записывает равенство значений косинуса 30 0
и
синуса 60 0
1б записывает равенство значений синуса и
косинуса 45 0
1б записывает равенство значений косинуса 60 0
и
синуса 30 0
Cos Sin
6
3
2
1
24
2
2
2
23
1
2
3
2
3 слайд
Новая тема. Исследование. Работа в парах. 1. Чему равен косинус углов ?; ; 6 4 3 2. Чему равен синус углов ? ; ; 6 4 3 3. Сделайте вывод. 3 2 1 ; ; 6 3 2 4 4 2 3 6 2 Cos Sin Cos Sin Cos Sin Дескрипторы: 1б записывает значения косинуса 30 0 и синуса 60 0 1б записывает значения синуса и косинуса 45 0 1б записывает значения косинуса 600 и синуса 30 0 1б записывает равенство значений косинуса 30 0 и синуса 60 0 1б записывает равенство значений синуса и косинуса 45 0 1б записывает равенство значений косинуса 60 0 и синуса 30 0 Cos Sin 6 3 2 1 24 2 2 2 23 1 2 3 2
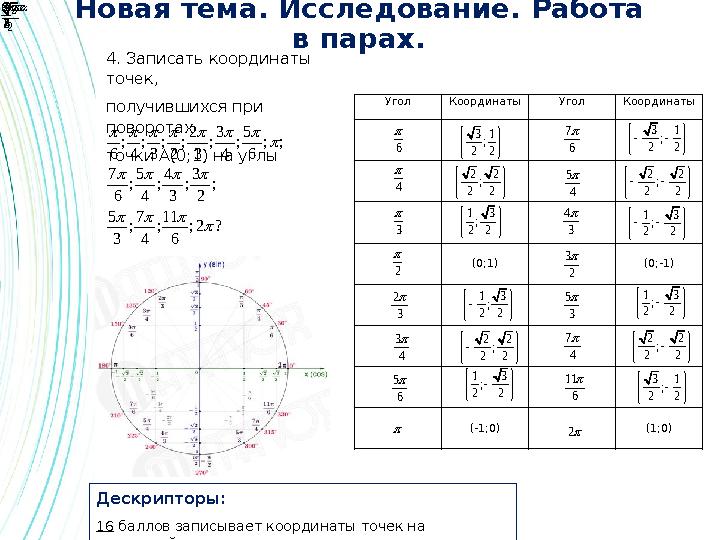
#4 слайд
Новая тема. Исследование. Работа
в парах.
Дескрипторы:
16 баллов записывает координаты точек на
единичной окружности 4. Записать координаты
точек,
получившихся при
поворотах
точки А(0;1) на углы 2 3 5 ; ; ; ; ; ; ; ;
6 4 3 2 3 4 6
7 5 4 3 ; ; ; ;
6 4 3 2
5 7 11 ; ; ; 2 ?
3 4 6
Угол Координаты Угол Координаты
(0;1) (0;-1)
(-1;0) (1;0)
6
3 1; 2 2
4
2 2; 2 2
3
1 3;2 2
2
2
3
1 3;2 2
3
4
2 2; 2 2
5
6
1 3;2 2
7
6
3 1; 2 2
5
4
2 2; 2 2
4
3
1 3;2 2
3
2
5
3
1 3;2 2
7
4
2 2; 2 2
11
6
3 1; 2 2
2
Cos Sin
6
3
2
1
24
2
2
2
23
1
2
3
2
4 слайд
Новая тема. Исследование. Работа в парах. Дескрипторы: 16 баллов записывает координаты точек на единичной окружности 4. Записать координаты точек, получившихся при поворотах точки А(0;1) на углы 2 3 5 ; ; ; ; ; ; ; ; 6 4 3 2 3 4 6 7 5 4 3 ; ; ; ; 6 4 3 2 5 7 11 ; ; ; 2 ? 3 4 6 Угол Координаты Угол Координаты (0;1) (0;-1) (-1;0) (1;0) 6 3 1; 2 2 4 2 2; 2 2 3 1 3;2 2 2 2 3 1 3;2 2 3 4 2 2; 2 2 5 6 1 3;2 2 7 6 3 1; 2 2 5 4 2 2; 2 2 4 3 1 3;2 2 3 2 5 3 1 3;2 2 7 4 2 2; 2 2 11 6 3 1; 2 2 2 Cos Sin 6 3 2 1 24 2 2 2 23 1 2 3 2

#5 слайд
Новая тема. Исследование. Работа
в парах.
Дескрипторы:
1б записывает, что угол любой величины можно изобразить на
единичной окружности
1б записывают, что область определения синуса и косинуса
есть любое число
1б записывают отрезок, в котором лежат все значения абсцисс
и ординат точек
1б записывают, что множество значений синуса и косинуса
есть отрезок от минус одного до одного. 5. Какие углы можно отметить на единичной окружности?
6. Какой вывод вы можете сделать?
7. Какие значения принимают абсциссы(косинус) и ординаты(синус) точек на
единичной окружности?
8. Какой вывод вы можете сделать?
Решение:
5. Сколь угодно большие и сколь угодно малые.
6. Область определения синуса и косинуса есть любое
число.
7. От 0 до 1.
8. Множество значений синуса и косинуса от минус 1 до 1
включительно.Cos Sin
6
3
2
1
24
2
2
2
23
1
2
3
2
5 слайд
Новая тема. Исследование. Работа в парах. Дескрипторы: 1б записывает, что угол любой величины можно изобразить на единичной окружности 1б записывают, что область определения синуса и косинуса есть любое число 1б записывают отрезок, в котором лежат все значения абсцисс и ординат точек 1б записывают, что множество значений синуса и косинуса есть отрезок от минус одного до одного. 5. Какие углы можно отметить на единичной окружности? 6. Какой вывод вы можете сделать? 7. Какие значения принимают абсциссы(косинус) и ординаты(синус) точек на единичной окружности? 8. Какой вывод вы можете сделать? Решение: 5. Сколь угодно большие и сколь угодно малые. 6. Область определения синуса и косинуса есть любое число. 7. От 0 до 1. 8. Множество значений синуса и косинуса от минус 1 до 1 включительно.Cos Sin 6 3 2 1 24 2 2 2 23 1 2 3 2

#6 слайд
Групповая
работа.Каковы область определения и множество значений
тангенса и котангенса?
Так как , то не может быть равным нулю.
Значит из всех значений надо убрать углы, при которых косинус равен нулю. То есть 90 0
, 270 0
,
такие же отрицательные и учесть повторение значений при совершении оборотов. Sin tg Cos
Cos
Так как , не может равняться нулю. И из всех значений надо убрать углы, при которых синус равен нулю.
Это 0 0
, 180 0
и противоположные им углы. Надо учесть, что при совершении оборотов получаются те же значения.
Множество значений этих функций будет любое число, так как в числителе и знаменателе дробей и
будут числа от минус единицы до плюс единицы.
Cos ctg Sin
Sin
Sin tg Cos
Sin tg Cos
Дескрипторы:
1б применяют формулу
1б делают вывод: косинус не равен нулю
1б выбирают углы 90 0
, 270 0
по единичной окружности
1б добавляют противоположные им углы
1б учитывают полные обороты
1б применяют формулу
1б делают вывод: синус не равен нулю
1б выбирают углы 0 0
, 180 0
на единичной окружности
1б добавляют противоположные им углы
1б учитывают полные обороты
1б применяют знания о множествах значений синуса и косинуса
1б записывают множества значений тангенса и котангенса
1б участие в работе группы ; 1б активное участие в работе группы ; 1б
лидер группы
Sin tg Cos
Cos ctg Sin
Cos Sin
6
3
2
1
24
2
2
2
23
1
2
3
2
6 слайд
Групповая работа.Каковы область определения и множество значений тангенса и котангенса? Так как , то не может быть равным нулю. Значит из всех значений надо убрать углы, при которых косинус равен нулю. То есть 90 0 , 270 0 , такие же отрицательные и учесть повторение значений при совершении оборотов. Sin tg Cos Cos Так как , не может равняться нулю. И из всех значений надо убрать углы, при которых синус равен нулю. Это 0 0 , 180 0 и противоположные им углы. Надо учесть, что при совершении оборотов получаются те же значения. Множество значений этих функций будет любое число, так как в числителе и знаменателе дробей и будут числа от минус единицы до плюс единицы. Cos ctg Sin Sin Sin tg Cos Sin tg Cos Дескрипторы: 1б применяют формулу 1б делают вывод: косинус не равен нулю 1б выбирают углы 90 0 , 270 0 по единичной окружности 1б добавляют противоположные им углы 1б учитывают полные обороты 1б применяют формулу 1б делают вывод: синус не равен нулю 1б выбирают углы 0 0 , 180 0 на единичной окружности 1б добавляют противоположные им углы 1б учитывают полные обороты 1б применяют знания о множествах значений синуса и косинуса 1б записывают множества значений тангенса и котангенса 1б участие в работе группы ; 1б активное участие в работе группы ; 1б лидер группы Sin tg Cos Cos ctg Sin Cos Sin 6 3 2 1 24 2 2 2 23 1 2 3 2

#7 слайд
Групповая
работа.
Оформите
таблицу:
Дескрипторы:
1б предлагает запись областей определения синуса и
косинуса и множеств значений тангенса и котангенса от
минус бесконечности до плюс бесконечности или множество
всех действительных чисел
1б предлагает запись множеств значений синуса и косинуса
в виде двойного нестрогого неравенства или в виде отрезка
1б предлагает запись области определения тангенса в виде
или где n – целое число
1б предлагает запись области определения котангенса в
виде
или , где 0 0 90 180 x n
2 x n
0 00 180 x n
x n n Z
Cos Sin
6
3
2
1
24
2
2
2
23
1
2
3
2
7 слайд
Групповая работа. Оформите таблицу: Дескрипторы: 1б предлагает запись областей определения синуса и косинуса и множеств значений тангенса и котангенса от минус бесконечности до плюс бесконечности или множество всех действительных чисел 1б предлагает запись множеств значений синуса и косинуса в виде двойного нестрогого неравенства или в виде отрезка 1б предлагает запись области определения тангенса в виде или где n – целое число 1б предлагает запись области определения котангенса в виде или , где 0 0 90 180 x n 2 x n 0 00 180 x n x n n Z Cos Sin 6 3 2 1 24 2 2 2 23 1 2 3 2

#8 слайд
Работа в
группах .
Найдите область определения и множество
значений функций:
1. y=Sin 3x
2. y=Cos 2x+5
3.
4.1
2
x
y tg
2 3 y ctgx
1.D (Sin 3x)=R, E(Sin 3x)= [-1;1]
2.D (Cos 2x +5)=R, E(Cos
2x+5)=[-4;6]
3. , E ( y )= R
4. , E ( y )= R
2
x n
x n Дескрипторы:
1б записывает D ( Sin 3 x )= R
1б записывает E ( Sin 3 x )= [-
1;1]
1б записывает D ( Cos 2 x
+5)= R
1б применяет E ( Cos x )=[-1;1]
1б записывает E ( Cos
2 x +5)=[-4;6]
1б записывает
1б записывает E(y)=R
1б записывает
1б записывает E(y)=R
2
x n
x n
Cos Sin
6
3
2
1
24
2
2
2
23
1
2
3
2
8 слайд
Работа в группах . Найдите область определения и множество значений функций: 1. y=Sin 3x 2. y=Cos 2x+5 3. 4.1 2 x y tg 2 3 y ctgx 1.D (Sin 3x)=R, E(Sin 3x)= [-1;1] 2.D (Cos 2x +5)=R, E(Cos 2x+5)=[-4;6] 3. , E ( y )= R 4. , E ( y )= R 2 x n x n Дескрипторы: 1б записывает D ( Sin 3 x )= R 1б записывает E ( Sin 3 x )= [- 1;1] 1б записывает D ( Cos 2 x +5)= R 1б применяет E ( Cos x )=[-1;1] 1б записывает E ( Cos 2 x +5)=[-4;6] 1б записывает 1б записывает E(y)=R 1б записывает 1б записывает E(y)=R 2 x n x n Cos Sin 6 3 2 1 24 2 2 2 23 1 2 3 2
#9 слайд
Домашнее
задание.
Найдите область определения и множество значений
функций:
1. y = Sin 3 x -1
2. y= 3 Cos 4 x +1
3. y=5+ tg 2x
4. y= 2-3ctg (x/2)Cos Sin
6
3
2
1
24
2
2
2
23
1
2
3
2
9 слайд
Домашнее задание. Найдите область определения и множество значений функций: 1. y = Sin 3 x -1 2. y= 3 Cos 4 x +1 3. y=5+ tg 2x 4. y= 2-3ctg (x/2)Cos Sin 6 3 2 1 24 2 2 2 23 1 2 3 2

шағым қалдыра аласыз
















