2024-2025 оқу жылына арналған
қысқа мерзімді сабақ жоспарларын
Жүктеп алғыңыз келеді ме?
ҚР Білім және Ғылым министірлігінің стандартымен жасалған
Тригонометриялық формулалар
Материал туралы қысқаша түсінік
мұғалімге көмекші құрал ретінде пайдалануына болады және адістемелік үлгі ретінде де пайлалануына болады.
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 16
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
Абай атындағы жалпы орта
білім беретін мектеп-лицей «Қосынды және айырым түрінде берілген
тригонометриялық функцияларды
көбейтінді түріне келтіру»
1 слайд
Абай атындағы жалпы орта білім беретін мектеп-лицей «Қосынды және айырым түрінде берілген тригонометриялық функцияларды көбейтінді түріне келтіру»
2 слайд
Білімділік: 1. Оқушыларға тригонометриялық функциялардың
қосындысы мен айырымын көбейтіндіге
түрлендіру формулаларын меңгерту;
2. Осы формулаларды есеп шығару кезінде қолдану
білу дағдыларын қалыптастыру.
Тәрбиелік: Оқушыларды өзара жарыстыра отырып, ойларын
жинақтау, есте сақтау қабілеттерін жетілдіру .
Дамытушылық: Оқушыларды көпшіл болуға үйрету, өзара көмегін
қалыптастыра отырып, өз біліміне ғана емес, өзге
оқушыныңда біліміне жауапкершілікпен қарауға
дағдыландыру, өзін- өзі басқаруға үйрету.
2 слайд
Білімділік: 1. Оқушыларға тригонометриялық функциялардың қосындысы мен айырымын көбейтіндіге түрлендіру формулаларын меңгерту; 2. Осы формулаларды есеп шығару кезінде қолдану білу дағдыларын қалыптастыру. Тәрбиелік: Оқушыларды өзара жарыстыра отырып, ойларын жинақтау, есте сақтау қабілеттерін жетілдіру . Дамытушылық: Оқушыларды көпшіл болуға үйрету, өзара көмегін қалыптастыра отырып, өз біліміне ғана емес, өзге оқушыныңда біліміне жауапкершілікпен қарауға дағдыландыру, өзін- өзі басқаруға үйрету.
3 слайд
I.Ұйымдастыру кезеңі.
II.Ой қозғау – үй тапсырмасын тексеру.
III. Ой толғау – жаңа сабақты өту.
IV. Ой түйін – есептер шығару.
V. Бағалау, қорытындылау.
VI. Үйге тапсырма беру.
3 слайд
I.Ұйымдастыру кезеңі. II.Ой қозғау – үй тапсырмасын тексеру. III. Ой толғау – жаңа сабақты өту. IV. Ой түйін – есептер шығару. V. Бағалау, қорытындылау. VI. Үйге тапсырма беру.
4 слайд
ІІ. Ой қозғау – Үй тапсырмасын
тексеру
Функцияны зерттеу алгоритімі бойынша
мына функцияны зерттеп, графигін
салыңдар:
у=х 3
+1
4 слайд
ІІ. Ой қозғау – Үй тапсырмасын тексеру Функцияны зерттеу алгоритімі бойынша мына функцияны зерттеп, графигін салыңдар: у=х 3 +1
5 слайд
ІІІ. Ой толғау – Жаңа тақырып.
«Қосынды және айырым түрінде берілген
тригонометриялық функцйяларды
көбейтінді түрінде келтіру».
5 слайд
ІІІ. Ой толғау – Жаңа тақырып. «Қосынды және айырым түрінде берілген тригонометриялық функцйяларды көбейтінді түрінде келтіру».
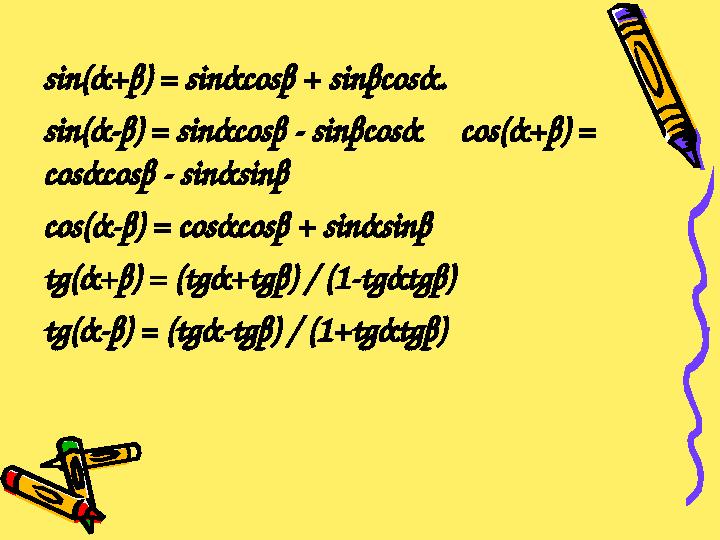
6 слайд
sin( ά + β ) = sin ά cos β + sin β cos ά .
sin( ά - β ) = sin ά cos β - sin β cos ά c os( ά + β ) =
cos ά cos β - sin ά sin β
cos( ά - β ) = cos ά cos β + sin ά sin β
tg( ά + β ) = (tg ά +tg β ) / (1-tg ά tg β )
tg( ά - β ) = (tg ά -tg β ) / (1+tg ά tg β )
6 слайд
sin( ά + β ) = sin ά cos β + sin β cos ά . sin( ά - β ) = sin ά cos β - sin β cos ά c os( ά + β ) = cos ά cos β - sin ά sin β cos( ά - β ) = cos ά cos β + sin ά sin β tg( ά + β ) = (tg ά +tg β ) / (1-tg ά tg β ) tg( ά - β ) = (tg ά -tg β ) / (1+tg ά tg β )
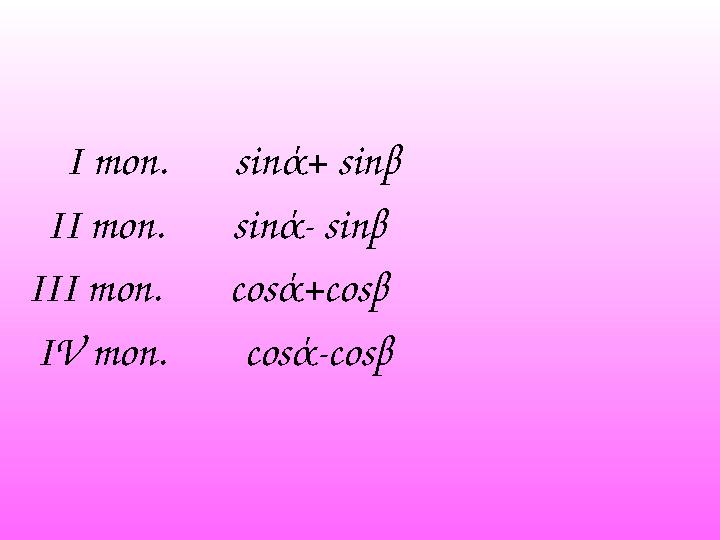
7 слайд
І топ. sin ά + sin β
ІІ топ. sin ά - sin β
ІІІ топ. cos ά +cos β
IV топ. cos ά - cos β
7 слайд
І топ. sin ά + sin β ІІ топ. sin ά - sin β ІІІ топ. cos ά +cos β IV топ. cos ά - cos β
8 слайд
I топ
sin ά +sin β = 2 sin (( ά + β )/2) со s (( ά - β )/2)
Ереже: Аргументтері әр түрлі синустың қосындысы
аргументтерінің қосындысының жартысының синусы
мен аргументтердің айырымының жартысының
косинусының екі еселенген көбейтіндісіне тең.
8 слайд
I топ sin ά +sin β = 2 sin (( ά + β )/2) со s (( ά - β )/2) Ереже: Аргументтері әр түрлі синустың қосындысы аргументтерінің қосындысының жартысының синусы мен аргументтердің айырымының жартысының косинусының екі еселенген көбейтіндісіне тең.
9 слайд
II топ
sin ά - sin β = 2 sin (( ά - β )/2) со s (( ά + β )/2)
Ереже: Аргументтері әр түрлі синустың
айырымы аргументтерінің жартысының синусы
мен аргументтердің қосындысының
жартысының косинусының екі еселенген
көбейтіндісіне тең.
9 слайд
II топ sin ά - sin β = 2 sin (( ά - β )/2) со s (( ά + β )/2) Ереже: Аргументтері әр түрлі синустың айырымы аргументтерінің жартысының синусы мен аргументтердің қосындысының жартысының косинусының екі еселенген көбейтіндісіне тең.
10 слайд
III топ
Со s ά +cos β = 2 cos (( ά + β )/2) со s (( ά - β )/2)
Ереже: Аргументтері әр түрлі екі косинустың
қосындысы аргументтерінің қосындысының
жартысының косинусы мен аргументтердің
айырымының жартысының косинусының екі
еселенген көбейтіндісіне тең.
10 слайд
III топ Со s ά +cos β = 2 cos (( ά + β )/2) со s (( ά - β )/2) Ереже: Аргументтері әр түрлі екі косинустың қосындысы аргументтерінің қосындысының жартысының косинусы мен аргументтердің айырымының жартысының косинусының екі еселенген көбейтіндісіне тең.
11 слайд
IV топ
c о s ά - cos β = - 2sin (( ά + β )/2) sin (( ά - β )/2)
Ереже: Аргументтері әр түрлі екі косинустың
айырымы аргументтердің қосындысының
жартысының синусы мен аргументтердің
айырымының жартысының синусының теріс
таңбамен алынған екі еселенген көбейтіндісіне
тең.
11 слайд
IV топ c о s ά - cos β = - 2sin (( ά + β )/2) sin (( ά - β )/2) Ереже: Аргументтері әр түрлі екі косинустың айырымы аргументтердің қосындысының жартысының синусы мен аргументтердің айырымының жартысының синусының теріс таңбамен алынған екі еселенген көбейтіндісіне тең.
12 слайд
ІІІ. Ой түйін – Есептер шығару.
I топ II топ III топ IV топ
№ 54 а ә б в
№ 55 б а в ә
12 слайд
ІІІ. Ой түйін – Есептер шығару. I топ II топ III топ IV топ № 54 а ә б в № 55 б а в ә
13 слайд
V.Бағалау,қорытындылау.
I топ II топ III топ IV топ
Үй тапсы.
Жаңа тақ.
Есеп шығ.
13 слайд
V.Бағалау,қорытындылау. I топ II топ III топ IV топ Үй тапсы. Жаңа тақ. Есеп шығ.
14 слайд
VI. Үйге тапсырма
tg( ά + β ) , tg( ά - β ) формулаларын
қорытып шығару.
№ 60
14 слайд
VI. Үйге тапсырма tg( ά + β ) , tg( ά - β ) формулаларын қорытып шығару. № 60
15 слайд
15 слайд
