Тригонометриялық функциялардың негізгі қасиеттері, 10-сынып
Материал туралы қысқаша түсінік
Слайдта тригонометриялық функциялардың негізгі қасиеттері қысқа да нұсқа жасалынған.
Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады
1 / 14
Сайтқа 5 материал жариялап, тегін АЛҒЫС ХАТ алыңыз!
Сайтқа 25 материал жариялап, тегін ҚҰРМЕТ ГРОМАТАСЫН алыңыз!
Материалдың қысқаша түсінігі
1 слайд
Тригонометриялық
функциялардың
негізгі қасиеттері
1 слайд
Тригонометриялық функциялардың негізгі қасиеттері
2 слайд
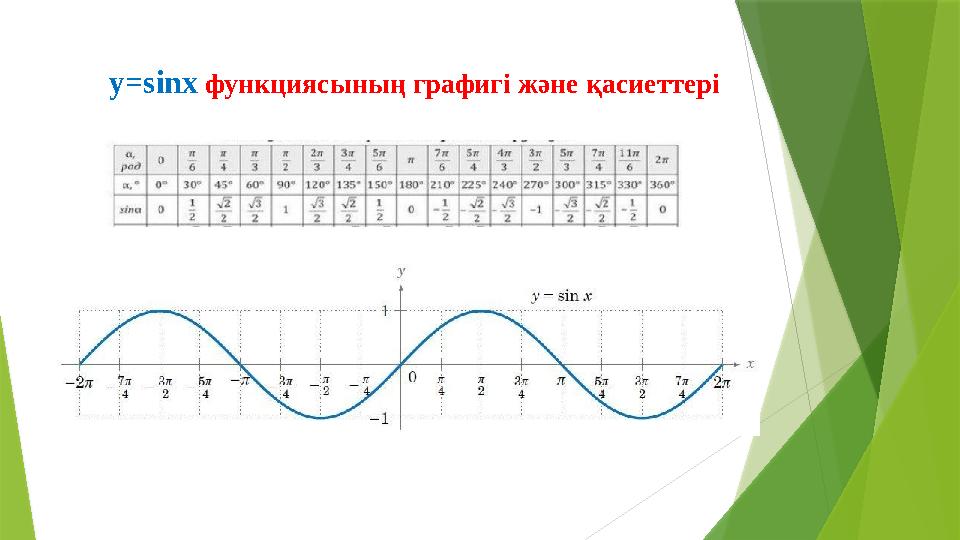
y=sinx функциясының графигі және қасиеттері
2 слайд
y=sinx функциясының графигі және қасиеттері
![1. Анықталу облысы D(x)= 2. Мәндер жиыны E(y)=[-1;1] 3. y=sinx–тақ функция. sin(-x)= -sinx. Графигі координатал](https://api.ust.kz/storage/files/materials/pptx/image/2024/november/d05/173082289075-3.jpeg "1. Анықталу облысы D(x)= 2. Мәндер жиыны E(y)=[-1;1] 3. y=sinx–тақ функция. sin(-x)= -sinx. Графигі координатал")
3 слайд
1. Анықталу облысы D(x)=
2. Мәндер жиыны E(y)=[-1;1]
3. y=sinx–тақ функция.
sin(-x)= -sinx. Графигі координаталар басына қарағанда симметриялы.
4. y=sinx–периодты функция. Ең кіші оң периоды 2-ге тең.
5. Ox және Oy өсімен қиылысу нүктелері:
Ox: sinx=0
x=0 , x=
x=k, k
Oy:
x=0 болса, sin0=0.
Онда Oy өсімен O(0;0) нүктесінде қиылысады.
3 слайд
1. Анықталу облысы D(x)= 2. Мәндер жиыны E(y)=[-1;1] 3. y=sinx–тақ функция. sin(-x)= -sinx. Графигі координаталар басына қарағанда симметриялы. 4. y=sinx–периодты функция. Ең кіші оң периоды 2-ге тең. 5. Ox және Oy өсімен қиылысу нүктелері: Ox: sinx=0 x=0 , x= x=k, k Oy: x=0 болса, sin0=0. Онда Oy өсімен O(0;0) нүктесінде қиылысады.
4 слайд
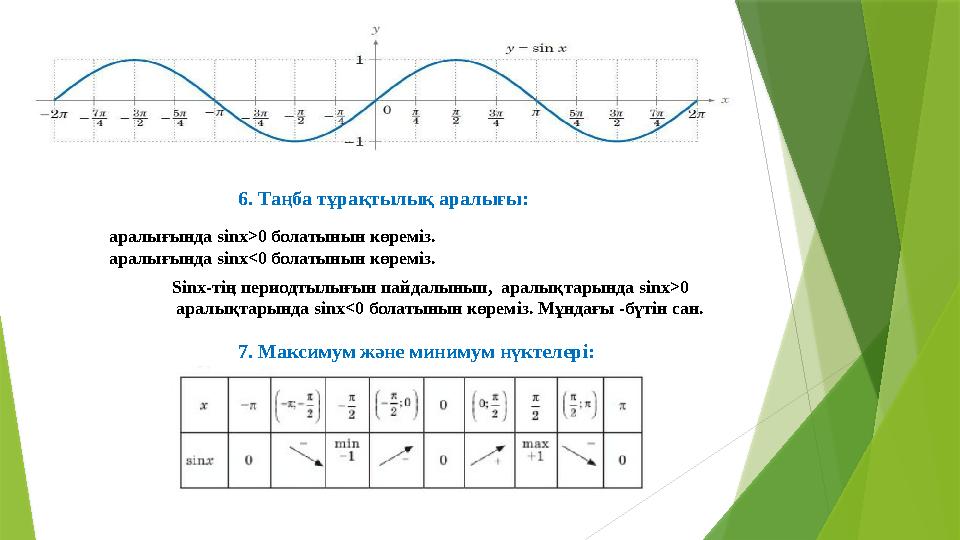
6. Таңба тұрақтылық аралығы:
аралығында sinx>0 болатынын көреміз.
аралығында sinx<0 болатынын көреміз.
Sinx-тің периодтылығын пайдалынып, аралықтарында sinx>0
аралықтарында sinx<0 болатынын көреміз. Мұндағы -бүтін сан.
7. Максимум және минимум нүктелері:
4 слайд
6. Таңба тұрақтылық аралығы: аралығында sinx>0 болатынын көреміз. аралығында sinx<0 болатынын көреміз. Sinx-тің периодтылығын пайдалынып, аралықтарында sinx>0 аралықтарында sinx<0 болатынын көреміз. Мұндағы -бүтін сан. 7. Максимум және минимум нүктелері:
5 слайд
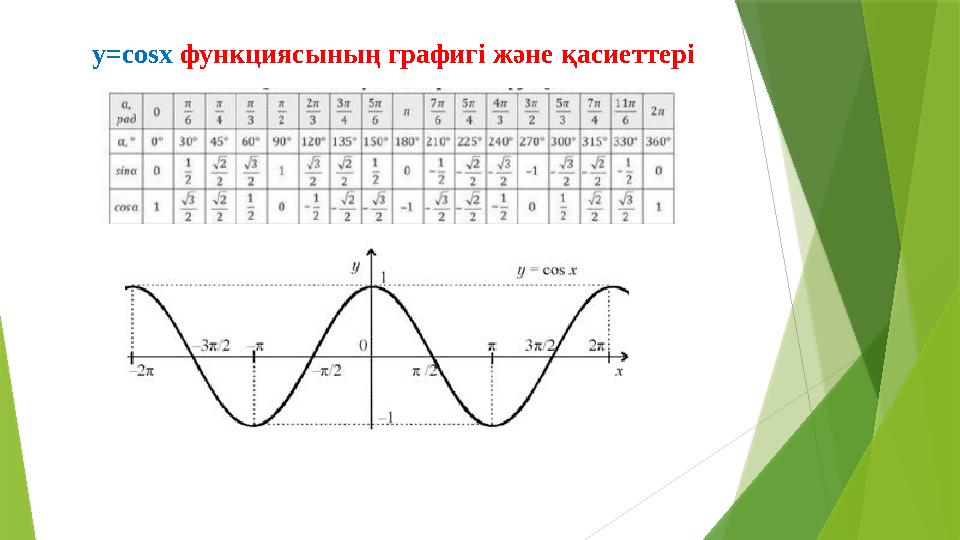
y=cosx функциясының графигі және қасиеттері
5 слайд
y=cosx функциясының графигі және қасиеттері
![1. Анықталу облысы D(x)= 2. Мәндер жиыны E(y)=[-1;1] 3. y=cosx–жұп функция. cos(-x)= cosx. Графигі Oy өсіне қар](https://api.ust.kz/storage/files/materials/pptx/image/2024/november/d05/173082289075-6.jpeg "1. Анықталу облысы D(x)= 2. Мәндер жиыны E(y)=[-1;1] 3. y=cosx–жұп функция. cos(-x)= cosx. Графигі Oy өсіне қар")
6 слайд
1. Анықталу облысы D(x)=
2. Мәндер жиыны E(y)=[-1;1]
3. y=cosx–жұп функция.
cos(-x)= cosx. Графигі Oy өсіне қарағанда симметриялы.
4. y=cosx–периодты функция. Ең кіші оң периоды 2-ге тең.
5. Ox және Oy өсімен қиылысу нүктелері:
Ox: cosx=0
x=
x= +, k
Oy:
x=0 болса, cos0=1.
Онда Oy өсімен O(0;1) нүктесінде қиылысады.
6 слайд
1. Анықталу облысы D(x)= 2. Мәндер жиыны E(y)=[-1;1] 3. y=cosx–жұп функция. cos(-x)= cosx. Графигі Oy өсіне қарағанда симметриялы. 4. y=cosx–периодты функция. Ең кіші оң периоды 2-ге тең. 5. Ox және Oy өсімен қиылысу нүктелері: Ox: cosx=0 x= x= +, k Oy: x=0 болса, cos0=1. Онда Oy өсімен O(0;1) нүктесінде қиылысады.
7 слайд
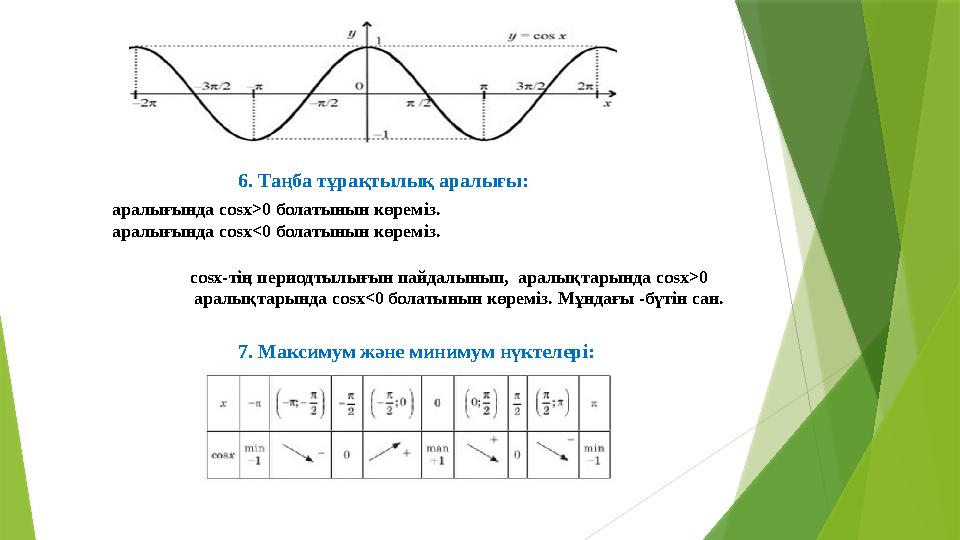
6. Таңба тұрақтылық аралығы:
аралығында cosx>0 болатынын көреміз.
аралығында cosx<0 болатынын көреміз.
cosx-тің периодтылығын пайдалынып, аралықтарында cosx>0
аралықтарында cosx<0 болатынын көреміз. Мұндағы -бүтін сан.
7. Максимум және минимум нүктелері:
7 слайд
6. Таңба тұрақтылық аралығы: аралығында cosx>0 болатынын көреміз. аралығында cosx<0 болатынын көреміз. cosx-тің периодтылығын пайдалынып, аралықтарында cosx>0 аралықтарында cosx<0 болатынын көреміз. Мұндағы -бүтін сан. 7. Максимум және минимум нүктелері:
8 слайд
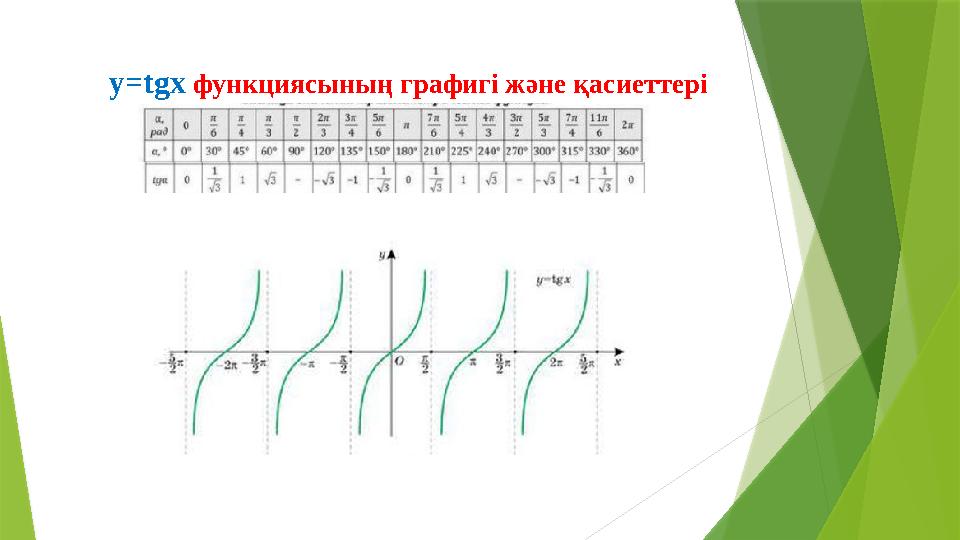
y=tgx функциясының графигі және қасиеттері
8 слайд
y=tgx функциясының графигі және қасиеттері
9 слайд
1. Анықталу облысы D(x)=
2. Мәндер жиыны E(y)=
3. y=tgx–тақ функция.
tg(-x)= -tgx. Графигі координаталар басына қарағанда симметриялы.
4. y=tgx–периодты функция. Ең кіші оң периоды -ге тең.
5. Ox және Oy өсімен қиылысу нүктелері:
Ox: tgx=0
x=k, k
Oy:
x=0 болса, tg0=0.
Онда Oy өсімен O(0;0) нүктесінде қиылысады.
9 слайд
1. Анықталу облысы D(x)= 2. Мәндер жиыны E(y)= 3. y=tgx–тақ функция. tg(-x)= -tgx. Графигі координаталар басына қарағанда симметриялы. 4. y=tgx–периодты функция. Ең кіші оң периоды -ге тең. 5. Ox және Oy өсімен қиылысу нүктелері: Ox: tgx=0 x=k, k Oy: x=0 болса, tg0=0. Онда Oy өсімен O(0;0) нүктесінде қиылысады.
10 слайд
6. Таңба тұрақтылық аралығы:
аралығында tgx<0 болатынын көреміз.
аралығында tgx>0 болатынын көреміз.
tgx-тің периодтылығын пайдалынып, аралықтарында tgx<0
аралықтарында tgx>0 болатынын көреміз. Мұндағы -бүтін сан.
10 слайд
6. Таңба тұрақтылық аралығы: аралығында tgx<0 болатынын көреміз. аралығында tgx>0 болатынын көреміз. tgx-тің периодтылығын пайдалынып, аралықтарында tgx<0 аралықтарында tgx>0 болатынын көреміз. Мұндағы -бүтін сан.
11 слайд
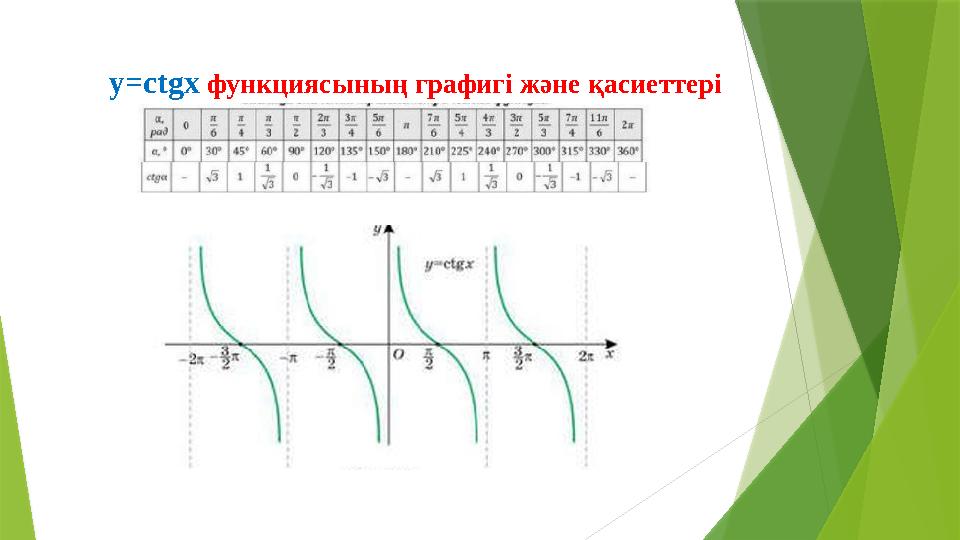
y=ctgx функциясының графигі және қасиеттері
11 слайд
y=ctgx функциясының графигі және қасиеттері
12 слайд
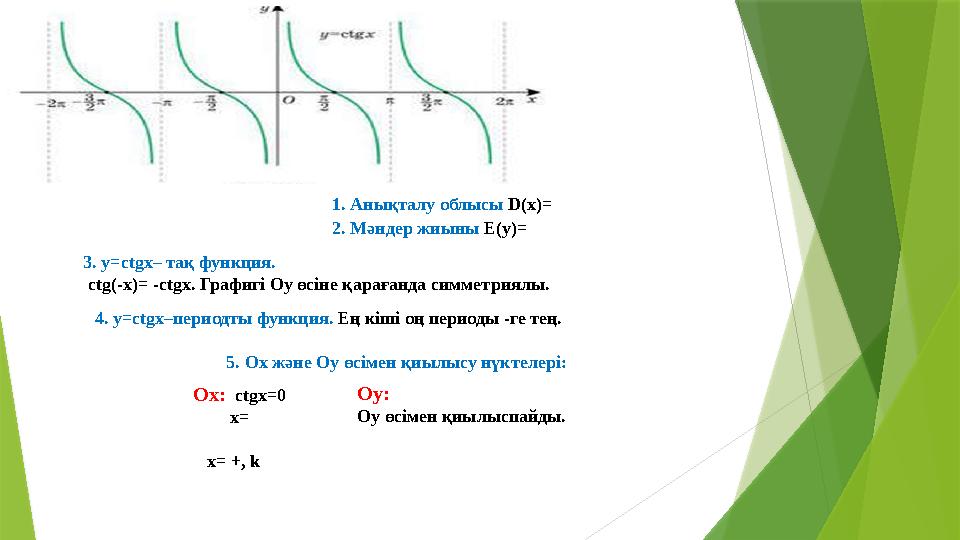
1. Анықталу облысы D(x)=
2. Мәндер жиыны E(y)=
3. y=ctgx– тақ функция.
ctg(-x)= -ctgx. Графигі Oy өсіне қарағанда симметриялы.
4. y=ctgx–периодты функция. Ең кіші оң периоды -ге тең.
5. Ox және Oy өсімен қиылысу нүктелері:
Ox: ctgx=0
x=
x= +, k
Oy:
Oy өсімен қиылыспайды.
12 слайд
1. Анықталу облысы D(x)= 2. Мәндер жиыны E(y)= 3. y=ctgx– тақ функция. ctg(-x)= -ctgx. Графигі Oy өсіне қарағанда симметриялы. 4. y=ctgx–периодты функция. Ең кіші оң периоды -ге тең. 5. Ox және Oy өсімен қиылысу нүктелері: Ox: ctgx=0 x= x= +, k Oy: Oy өсімен қиылыспайды.
13 слайд
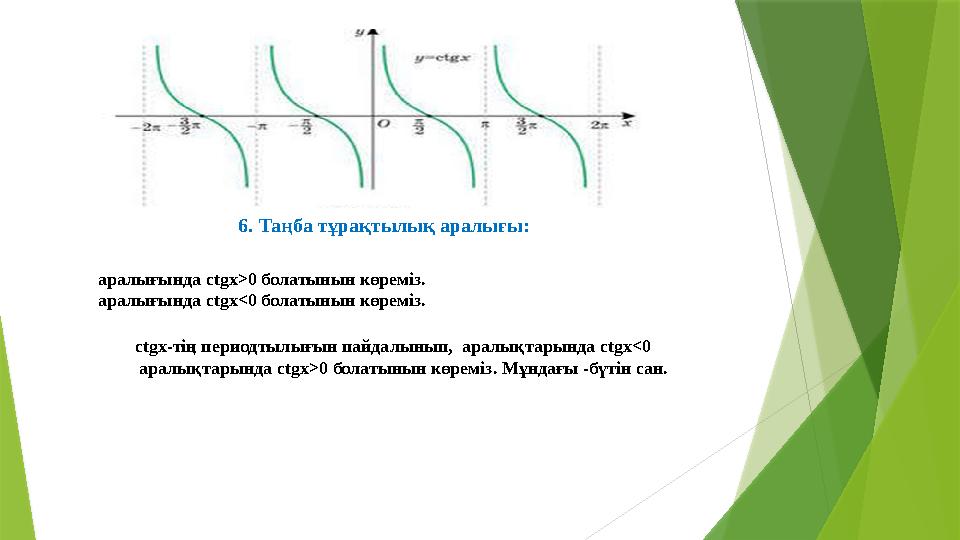
6. Таңба тұрақтылық аралығы:
аралығында ctgx>0 болатынын көреміз.
аралығында ctgx<0 болатынын көреміз.
ctgx-тің периодтылығын пайдалынып, аралықтарында ctgx<0
аралықтарында ctgx>0 болатынын көреміз. Мұндағы -бүтін сан.
13 слайд
6. Таңба тұрақтылық аралығы: аралығында ctgx>0 болатынын көреміз. аралығында ctgx<0 болатынын көреміз. ctgx-тің периодтылығын пайдалынып, аралықтарында ctgx<0 аралықтарында ctgx>0 болатынын көреміз. Мұндағы -бүтін сан.
