Тригонометриялық теңдеулер жүйесін шешу

1 слайд
Сабақ тақырыбы: Оқу мақсаты: Тригонометриялық теңдеулер жүйесін шешу 10.2.3.16 Тригонометриялық теңдеулер жүйесін шеше білу; Сабақ мақсаты: Тригонометриялық теңдеулер жүйесін шешуді үйрету.

1 слайд

2 слайд
Бағалау критерийлері - Теңдеулер жүйесін шешудің әдістерін біледі; - Берілген тригонометриялық теңдеулер жүйесінің түрін ажырата алады; - Тригонометриялық теңдеулер жүйесін шығара біледі;

2 слайд

3 слайд
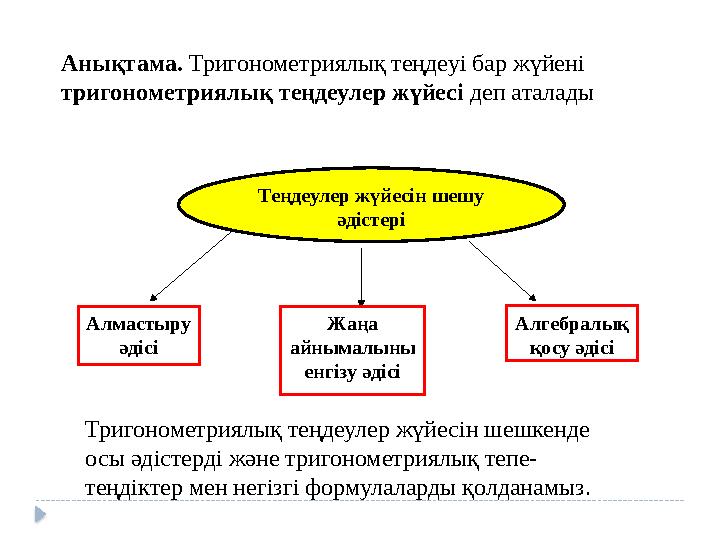
Анықтама. Тригонометриялық теңдеуі бар жүйені тригонометриялық теңдеулер жүйесі деп аталады Теңдеулер жүйесін шешу әдістері Алмастыру әдісі Жаңа айнымалыны енгізу әдісі Алгебралық қосу әдісі Тригонометриялық теңдеулер жүйесін шешкенде осы әдістерді және тригонометриялық тепе- теңдіктер мен негізгі формулаларды қолданамыз.

3 слайд

4 слайд
Әр түрлі тригонометриялық теңдеулер жүйесінін шешу әдістері І түрі   ІІ түрі.     Бұндай түрдегі берілген теңдеулер жүйесін шешу үшін бірінші теңдеудегі қосындыны немесе айырымды көбейтінді түріне келтіреміз. Бұндай түрдегі берілген теңдеулер жүйесін шешу үшін көбейтіндіні қосындыға түрлендіру формуласын қолданамыз.

4 слайд

5 слайд
ІІІ түрі. Бұндай теңдеулер жүйесін шешу үшін u = белгілеулерін енгізіп, ⇒жүйесін аламыз.  

5 слайд

6 слайд
ІV түрі. (1) түріндегі теңдеулерді шешу үшін теңдеулерді бір-біріне қосып және азайту арқылы және түріне келтіреміз.   2) Бұл теңдеулерді шешу үшін бірінші теңдеуді екінші теңдеуге бөліп, (1)жүйенің түріне келтіреміз.   3) түріндегі жүйелерді шешу үшін оның бірінші теңдеуін екіншісіне бөліп, теңдеуінен х-тің мәнін тауып, оны берілген жүйенің біреуіне қойып у-ті табуға болады.

6 слайд

7 слайд
Әр түрлі тригонометриялық теңдеулер жүйесінің шешу әдістері •І түрі.   Бұндай түрдегі берілген теңдеулер жүйесін шешу үшін бірінші теңдеудегі қосындыны немесе айырымды көбейтінді түріне келтіреміз. 1-мысал.теңдеулер жүйесін

7 слайд

8 слайд
Шешуі: Бірінші теңдеудегі косинустардың айырымын көбейтінгдіге түрлендіру формуласын қолданамыз: ⇒⇒⇒⇒ Алмастыру әдісі бойынша екінші теңдеудегі x-тіy арқылы өрнектеп, оны бірінші теңдеудегі x-тің орнына қоямыз: - 2y = y =    

8 слайд

9 слайд
x = Егер n = 2kболса, онда х = Егер n = 2k + 1 болса, онда х = y= - Жауабы:

9 слайд

10 слайд
Шешуі: sin 2 x = 1 – cos 2 формуласын қолданып, түріне келтіріп, u = белгілеулерін енгіземіз. ⇒ u 1 = 0, v 1 = u 2 = , v 2 = 0 . Табылған бұл мәндерді белгілеудегі u мен v-ның орнына қойып x пен у-тің мәндерін табамыз: ⇒ ⇒ Жауабы: 2-мысал

10 слайд

11 слайд
4-мысал. теңдеулер жүйесін шешейік. Шешуі: Жауабы: , . 3 - мысал

11 слайд

12 слайд
4- мысал

12 слайд

13 слайд
Жаңа тақырыпты бекітуге арналған тапсырмалар

13 слайд

14 слайд
Жұптық жұмыс І. ІІ. ІІІ. Өздігінен орындауға ұсынылатын теңдеулер жүйесі  Дескриптор: Тригонометриялық теңдеулер жүйесінің түрлерін анықтай алады; Тригонометриялық теңдеулер жүйесін шешуде тригонометриялық формулаларды пайдалана алады; Тригонометриялық теңдеулер жүйесінің шешімін табады.

14 слайд

15 слайд
Рефлексия: Бүгін мен ................ білдім Маған ........ қызықты болды Маған ..................... қиын болды Мен ......... тапсырманы орындадым Мен .................................... түсіндім Енді мен ..........................................

15 слайд