Материалдар / Тригонометриялық теңсіздіктер

Тригонометриялық теңсіздіктер

Материал туралы қысқаша түсінік

Нурмуханбетова Дария Уахитовна

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

04 Қараша 2024

1 рет жүктелген

Алгебра Презентация 10 сынып

450 ₸

Бүгін алсаңыз
+23 бонус беріледі
Бұл не?

Бүгін алсаңыз +23 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 32

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Тригонометриялық теңсіздіктер Сабақтың тақырыбы: Оқу мақсаты: 10.2.4.7 Қарапайым тригонометриялық теңсіздіктерді шешеді;

1 слайд

Тригонометриялық теңсіздіктер Сабақтың тақырыбы: Оқу мақсаты: 10.2.4.7 Қарапайым тригонометриялық теңсіздіктерді шешеді;

2 слайд
қарапайым тригонометриялық теңсіздіктерді бірлік шеңберді қолданып шығара алады; қарапайым тригонометриялық теңсіздіктерді графикалық тәсілмен шығара алады; қарапайым тригонометриялық теңсіздіктерді дайын формула қолданып шығара алады; Қарапайым тригонометриялық теңсіздіктерді шешуді әртүрлі тәсілмен шешуді үйрету. Сабақ мақсаты: Бағалау критерийі:

2 слайд

қарапайым тригонометриялық теңсіздіктерді бірлік шеңберді қолданып шығара алады; қарапайым тригонометриялық теңсіздіктерді графикалық тәсілмен шығара алады; қарапайым тригонометриялық теңсіздіктерді дайын формула қолданып шығара алады; Қарапайым тригонометриялық теңсіздіктерді шешуді әртүрлі тәсілмен шешуді үйрету. Сабақ мақсаты: Бағалау критерийі:

3 слайд
Барлық қарапайым тригонометриялық теңсіздіктерді : шешудің бірақ тәсілі бар 1. Теңсіздіктің шешімін қанағаттандыратын координатаны бірлік шеңберде белгілейміз және ; доғаны саламыз 2. Осы доға бойынан бастапқы нүктесін табамыз ( ) салу тек қана сағат тіліне қарсы жүргізіледі 3. Салынған доға бойымен сағат тіліне қарсы жүріп соңғы нүктесін табамыз 4. Доға бойынан бастапқы нүктесі мен соңғы нүктесін тапқаннан кейін теңсіздіктің шешу жолы мен жауабын жазамыз. Қарапайым тригонометриялық теңсіздіктерді бірлік шеңберді қолданып шығару;

3 слайд

Барлық қарапайым тригонометриялық теңсіздіктерді : шешудің бірақ тәсілі бар 1. Теңсіздіктің шешімін қанағаттандыратын координатаны бірлік шеңберде белгілейміз және ; доғаны саламыз 2. Осы доға бойынан бастапқы нүктесін табамыз ( ) салу тек қана сағат тіліне қарсы жүргізіледі 3. Салынған доға бойымен сағат тіліне қарсы жүріп соңғы нүктесін табамыз 4. Доға бойынан бастапқы нүктесі мен соңғы нүктесін тапқаннан кейін теңсіздіктің шешу жолы мен жауабын жазамыз. Қарапайым тригонометриялық теңсіздіктерді бірлік шеңберді қолданып шығару;

4 слайд
Шешу алгоритмі 1. Егер аргумент күрделі болса (х тен басқа ), онда оны t – мен ауыстырамыз; 2. tOy координаттық жүйеде y=sint (т.б.) және y=a функциялардың графиктерін саламыз; 3. екі көршілес қиылысу нүктелерін анықтаймыз (Оу осіне жақырынақ орналасқан); 4. Синус (т.б.) функцияның периодын ала отырып, t аргументті анықтайтың қос теңсіздік жазамыз; 5. Қайта өзіміздің х айнымалымызға оралып, қос теңсіздіктін шешімін сандық аралық түрінде жазамыз. Қарапайым тригонометриялық теңсіздіктерді графикалық тәсілмен шығара алады;

4 слайд

Шешу алгоритмі 1. Егер аргумент күрделі болса (х тен басқа ), онда оны t – мен ауыстырамыз; 2. tOy координаттық жүйеде y=sint (т.б.) және y=a функциялардың графиктерін саламыз; 3. екі көршілес қиылысу нүктелерін анықтаймыз (Оу осіне жақырынақ орналасқан); 4. Синус (т.б.) функцияның периодын ала отырып, t аргументті анықтайтың қос теңсіздік жазамыз; 5. Қайта өзіміздің х айнымалымызға оралып, қос теңсіздіктін шешімін сандық аралық түрінде жазамыз. Қарапайым тригонометриялық теңсіздіктерді графикалық тәсілмен шығара алады;

5 слайд
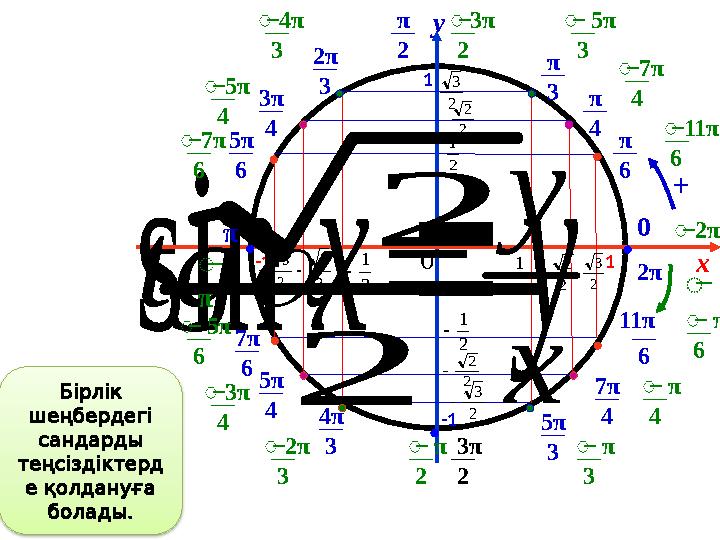
x y 0 2 1 2 1 2 1  2 1  2 2  2 2  2 2 2 2 2 3 2 3 2 3  2 3  1-1 1 -1 yxsin x y tg x y tg 2 2 — π 6 — π 4 — π 3 — π 2 — 2π 3 — 3π 4 — 5π 6 π 0 — 5π 4 — 7π 6 — 4π 3 — 3π 2 — 7π 4 — 5π 3 — 11π 6 — ̶ 3π 2 — ̶ 5π 3 — ̶ 7π 4 — ̶ 11π 6 ̶ 2π — ̶ π 6 — ̶ π 4 — ̶ π 3 — ̶ π 2 — ̶ 2π 3 — ̶ 3π 4 — ̶ 5π 6 ̶ π — ̶ 7π 6 — ̶ 5π 4 — ̶ 4π 3 2π ̶ + Бірлік шеңбердегі сандарды теңсіздіктерд е қолдануға . болады

5 слайд

x y 0 2 1 2 1 2 1  2 1  2 2  2 2  2 2 2 2 2 3 2 3 2 3  2 3  1-1 1 -1 yxsin x y tg x y tg 2 2 — π 6 — π 4 — π 3 — π 2 — 2π 3 — 3π 4 — 5π 6 π 0 — 5π 4 — 7π 6 — 4π 3 — 3π 2 — 7π 4 — 5π 3 — 11π 6 — ̶ 3π 2 — ̶ 5π 3 — ̶ 7π 4 — ̶ 11π 6 ̶ 2π — ̶ π 6 — ̶ π 4 — ̶ π 3 — ̶ π 2 — ̶ 2π 3 — ̶ 3π 4 — ̶ 5π 6 ̶ π — ̶ 7π 6 — ̶ 5π 4 — ̶ 4π 3 2π ̶ + Бірлік шеңбердегі сандарды теңсіздіктерд е қолдануға . болады

6 слайд
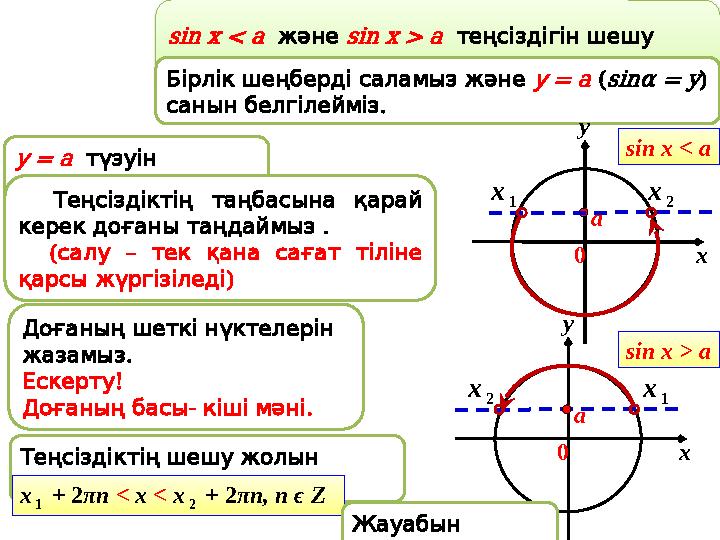
sin x < a және sin x > a теңсіздігін шешу : алгоритмі Бірлік шеңберді саламыз және =у a (sinα = y) . санын белгілейміз y х0 a =у a түзуін жүргіземіз y х0 sin x < a sin x > a a Теңсіздіктің таңбасына қарай . керек доғаны таңдаймыз ( – салу тек қана сағат тіліне ) қарсы жүргізіледі Доғаның шеткі нүктелерін . жазамыз ! Ескерту - . Доғаның басы кіші мәні х 2 х 1 х 1 х 2 Теңсіздіктің шешу жолын жазамыз х 1 + 2πn < x < х 2 + 2πn, n ϵ Z Жауабын жазамыз

6 слайд

sin x < a және sin x > a теңсіздігін шешу : алгоритмі Бірлік шеңберді саламыз және =у a (sinα = y) . санын белгілейміз y х0 a =у a түзуін жүргіземіз y х0 sin x < a sin x > a a Теңсіздіктің таңбасына қарай . керек доғаны таңдаймыз ( – салу тек қана сағат тіліне ) қарсы жүргізіледі Доғаның шеткі нүктелерін . жазамыз ! Ескерту - . Доғаның басы кіші мәні х 2 х 1 х 1 х 2 Теңсіздіктің шешу жолын жазамыз х 1 + 2πn < x < х 2 + 2πn, n ϵ Z Жауабын жазамыз

7 слайд
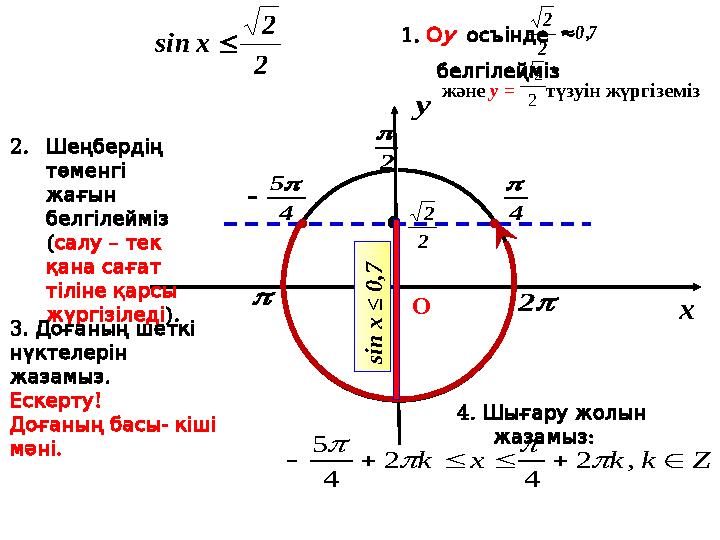
x y 2   2 2 2 xsin 2 24 5  4  1. О у осъінде белгілейміз 7,0 2 2  2. Шеңбердің төменгі жағын белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі). 3. Доғаның шеткі нүктелерін . жазамыз ! Ескерту - Доғаның басы кіші . мәні Zkkxk  ,2 4 2 4 5     2 2 4. Шығару жолын : жазамыз О және у = түзуін жүргіземіз s i n x ≤ 0 ,7

7 слайд

x y 2   2 2 2 xsin 2 24 5  4  1. О у осъінде белгілейміз 7,0 2 2  2. Шеңбердің төменгі жағын белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі). 3. Доғаның шеткі нүктелерін . жазамыз ! Ескерту - Доғаның басы кіші . мәні Zkkxk  ,2 4 2 4 5     2 2 4. Шығару жолын : жазамыз О және у = түзуін жүргіземіз s i n x ≤ 0 ,7

8 слайд
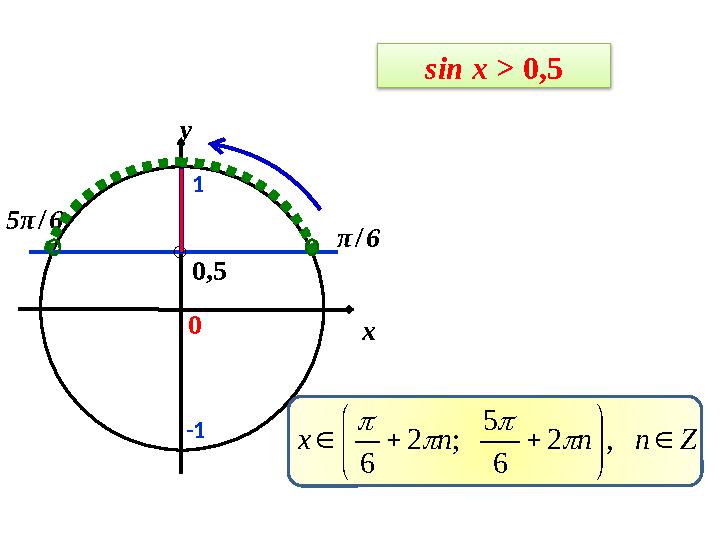
sin x > 0,5 0,5 π ̸ 6 5π ̸ 6 -1 1 Znnnx        ,2 6 5 ;2 6     x y 0

8 слайд

sin x > 0,5 0,5 π ̸ 6 5π ̸ 6 -1 1 Znnnx        ,2 6 5 ;2 6     x y 0

9 слайд
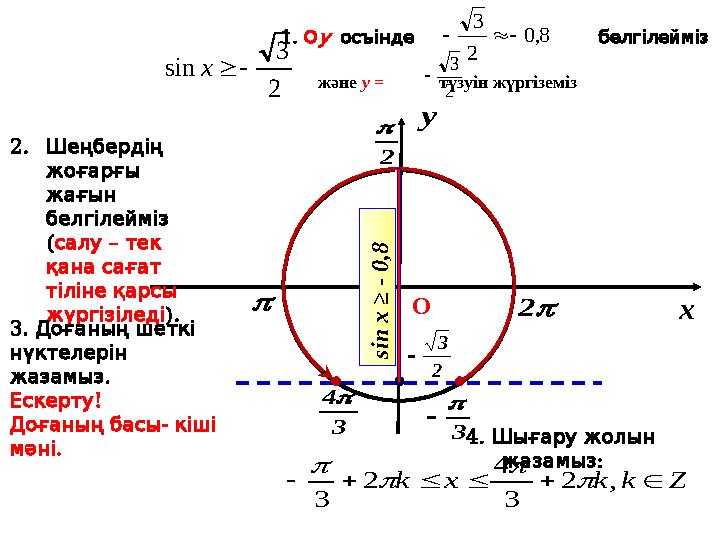
x y 2   2 2 3 sinx 2 3  3 4 3   8,0 2 3  Zkkxk  ,2 3 4 2 3     2 3  О s i n x ≥ - 0 ,8 1. Оу осъінде белгілейміз және у = түзуін жүргіземіз 2. Шеңбердің жоғарғы жағын белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі). 3. Доғаның шеткі нүктелерін . жазамыз ! Ескерту - Доғаның басы кіші . мәні 4. Шығару жолын : жазамыз

9 слайд

x y 2   2 2 3 sinx 2 3  3 4 3   8,0 2 3  Zkkxk  ,2 3 4 2 3     2 3  О s i n x ≥ - 0 ,8 1. Оу осъінде белгілейміз және у = түзуін жүргіземіз 2. Шеңбердің жоғарғы жағын белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі). 3. Доғаның шеткі нүктелерін . жазамыз ! Ескерту - Доғаның басы кіші . мәні 4. Шығару жолын : жазамыз

10 слайд
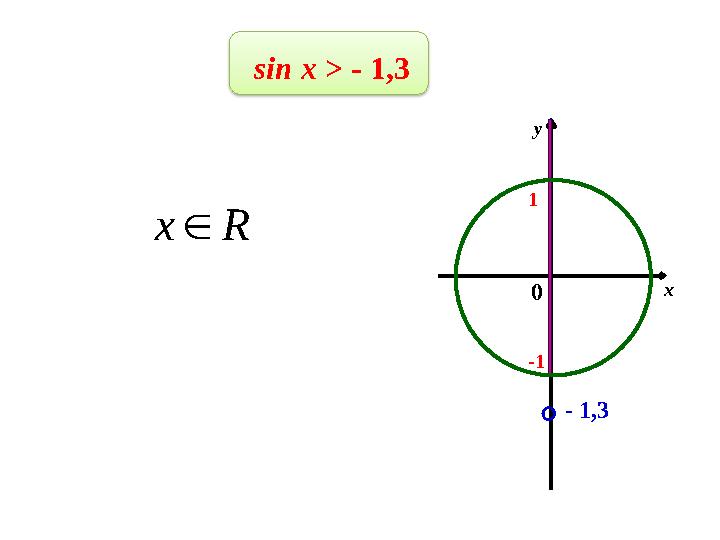
sin x > - 1,3 x y -1 1 - 1,3 Rx ○ 0

10 слайд

sin x > - 1,3 x y -1 1 - 1,3 Rx ○ 0

11 слайд
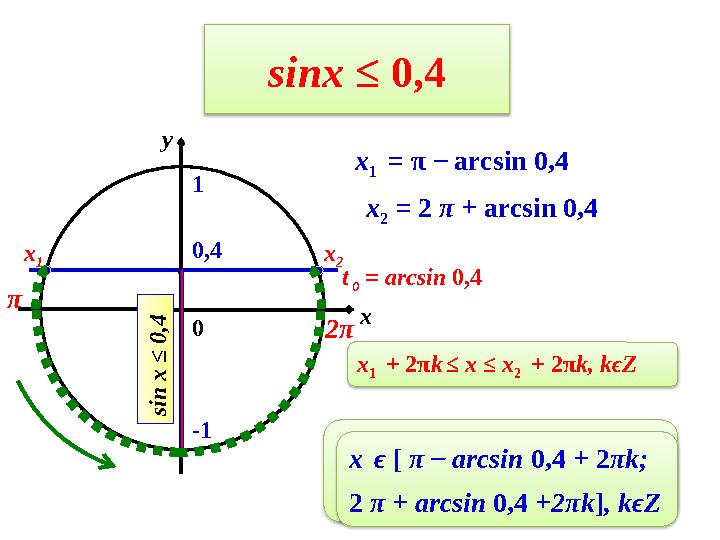
sinx ≤ 0,4 0 x y x 1 = π ̶ arcsin 0,4 0,4 x 2 x 1 -1 1 x 2 = 2 π + arcsin 0,4 x ϵ [ π ̶ arcsin 0,4 + 2πk; 2 π + arcsin 0,4 +2πk], kϵZ t 0 = arcsin 0,4 π 2π s i n x ≤ 0 ,4 x 1 + 2πk ≤ x ≤ x 2 + 2πk, kϵZ

11 слайд

sinx ≤ 0,4 0 x y x 1 = π ̶ arcsin 0,4 0,4 x 2 x 1 -1 1 x 2 = 2 π + arcsin 0,4 x ϵ [ π ̶ arcsin 0,4 + 2πk; 2 π + arcsin 0,4 +2πk], kϵZ t 0 = arcsin 0,4 π 2π s i n x ≤ 0 ,4 x 1 + 2πk ≤ x ≤ x 2 + 2πk, kϵZ

12 слайд
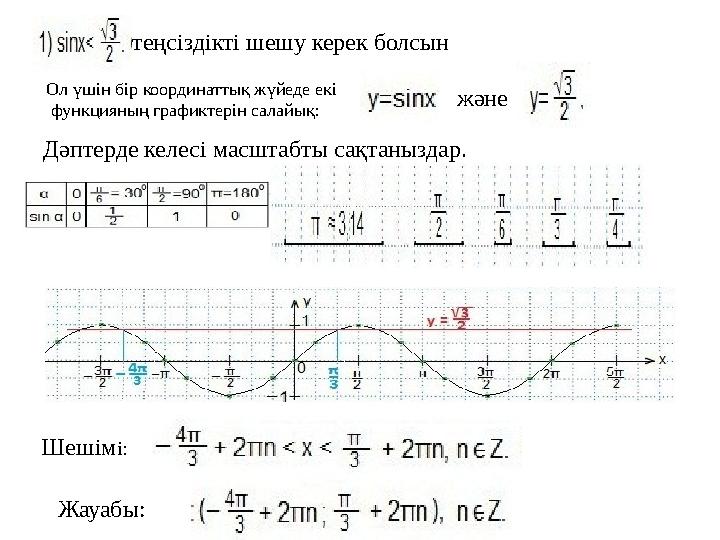
теңсіздікті шешу керек болсын Ол үшін бір координаттық жүйеде екі функцияның графиктерін салайық: және Дәптерде келесі масштабты сақтаныздар. Шешімі: Жауабы:

12 слайд

теңсіздікті шешу керек болсын Ол үшін бір координаттық жүйеде екі функцияның графиктерін салайық: және Дәптерде келесі масштабты сақтаныздар. Шешімі: Жауабы:

13 слайд
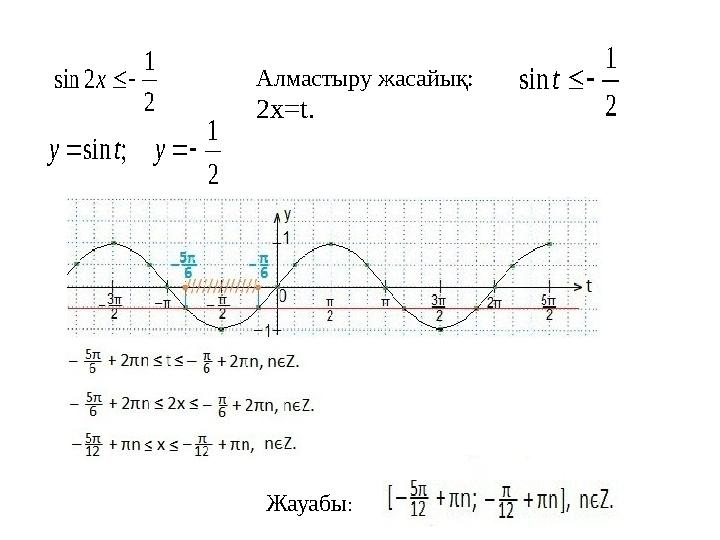
Алмастыру жасайық: 2х=t. 2 1 sint 2 1 ;sin  yty 2 1 2sinx Жауабы:

13 слайд

Алмастыру жасайық: 2х=t. 2 1 sint 2 1 ;sin  yty 2 1 2sinx Жауабы:

14 слайд
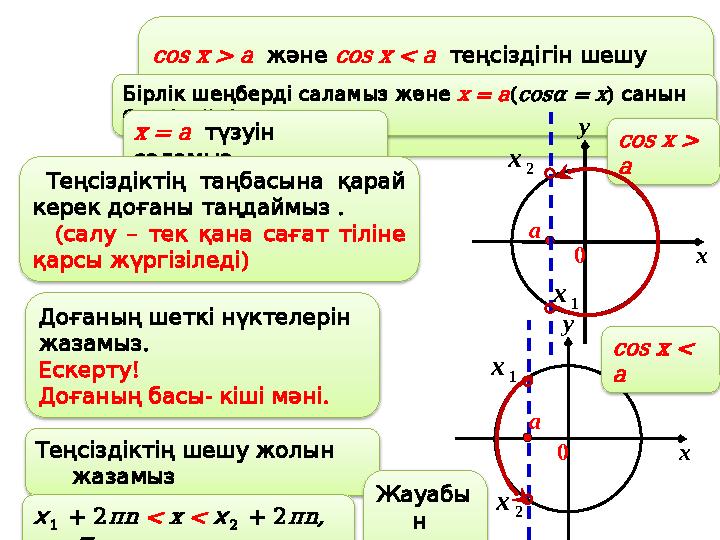
cos x > a және cos x < a теңсіздігін шешу : алгоритмі Бірлік шеңберді саламыз және x = a(cosα = x) санын белгілейміз y х0 a x = a түзуін саламыз y х0 cos x > a cos x < a a Теңсіздіктің таңбасына қарай . керек доғаны таңдаймыз ( – салу тек қана сағат тіліне ) қарсы жүргізіледі Доғаның шеткі нүктелерін . жазамыз ! Ескерту - . Доғаның басы кіші мәні х 2 х 1 х 1 х 2 Теңсіздіктің шешу жолын жазамыз х 1 + 2πn < x < х 2 + 2πn, n ϵ Z Жауабы н жазамы з

14 слайд

cos x > a және cos x < a теңсіздігін шешу : алгоритмі Бірлік шеңберді саламыз және x = a(cosα = x) санын белгілейміз y х0 a x = a түзуін саламыз y х0 cos x > a cos x < a a Теңсіздіктің таңбасына қарай . керек доғаны таңдаймыз ( – салу тек қана сағат тіліне ) қарсы жүргізіледі Доғаның шеткі нүктелерін . жазамыз ! Ескерту - . Доғаның басы кіші мәні х 2 х 1 х 1 х 2 Теңсіздіктің шешу жолын жазамыз х 1 + 2πn < x < х 2 + 2πn, n ϵ Z Жауабы н жазамы з

15 слайд
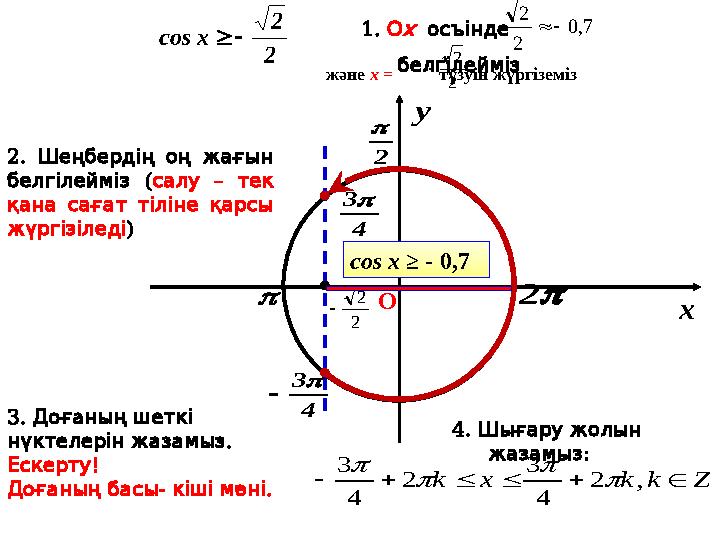
x y 2   2 2 2 xcos 2 2  4 3 4 3  7,0 2 2  2. Шеңбердің оң жағын ( белгілейміз – салу тек қана сағат тіліне қарсы жүргізіледі) 3. Доғаның шеткі . нүктелерін жазамыз ! Ескерту - . Доғаның басы кіші мәні Zkkxk  ,2 4 3 2 4 3     2 2  О cos x ≥ - 0,7 4. Шығару жолын : жазамыз 1. О х осъінде белгілейміз және х = түзуін жүргіземіз

15 слайд

x y 2   2 2 2 xcos 2 2  4 3 4 3  7,0 2 2  2. Шеңбердің оң жағын ( белгілейміз – салу тек қана сағат тіліне қарсы жүргізіледі) 3. Доғаның шеткі . нүктелерін жазамыз ! Ескерту - . Доғаның басы кіші мәні Zkkxk  ,2 4 3 2 4 3     2 2  О cos x ≥ - 0,7 4. Шығару жолын : жазамыз 1. О х осъінде белгілейміз және х = түзуін жүргіземіз

16 слайд
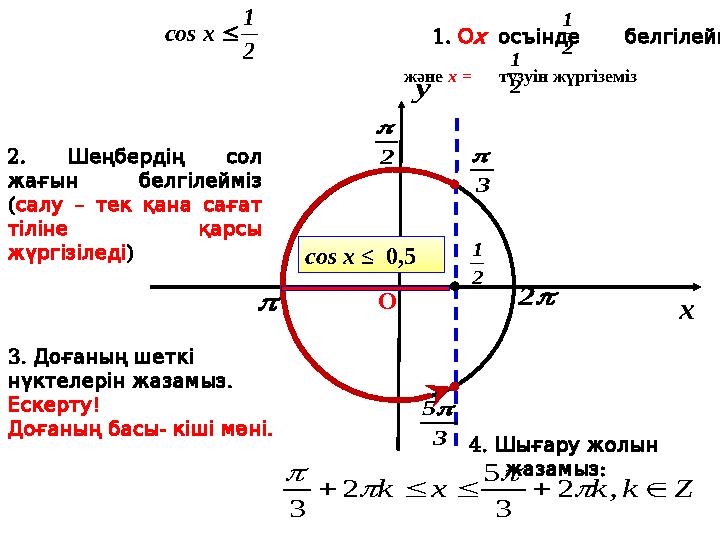
x y 2   2 2 1 xcos 2 1 3 5 3  2 1 2. Шеңбердің сол жағын белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі) Zkkxk  ,2 3 5 2 3     2 1 О cos x ≤ 0,5 1. О х осъінде белгілейміз және х = түзуін жүргіземіз 3. Доғаның шеткі . нүктелерін жазамыз ! Ескерту - . Доғаның басы кіші мәні 4. Шығару жолын : жазамыз

16 слайд

x y 2   2 2 1 xcos 2 1 3 5 3  2 1 2. Шеңбердің сол жағын белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі) Zkkxk  ,2 3 5 2 3     2 1 О cos x ≤ 0,5 1. О х осъінде белгілейміз және х = түзуін жүргіземіз 3. Доғаның шеткі . нүктелерін жазамыз ! Ескерту - . Доғаның басы кіші мәні 4. Шығару жолын : жазамыз

17 слайд
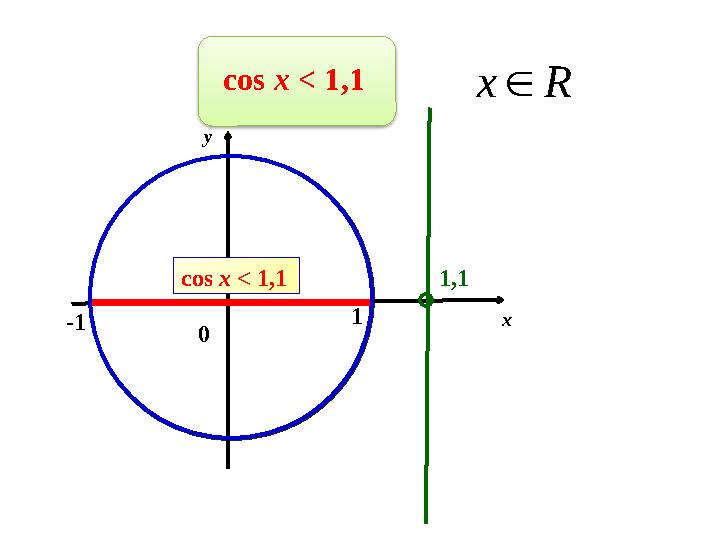
0 -1 1 x y cos х < 1,1 1,1 cos х < 1,1 Rx

17 слайд

0 -1 1 x y cos х < 1,1 1,1 cos х < 1,1 Rx

18 слайд
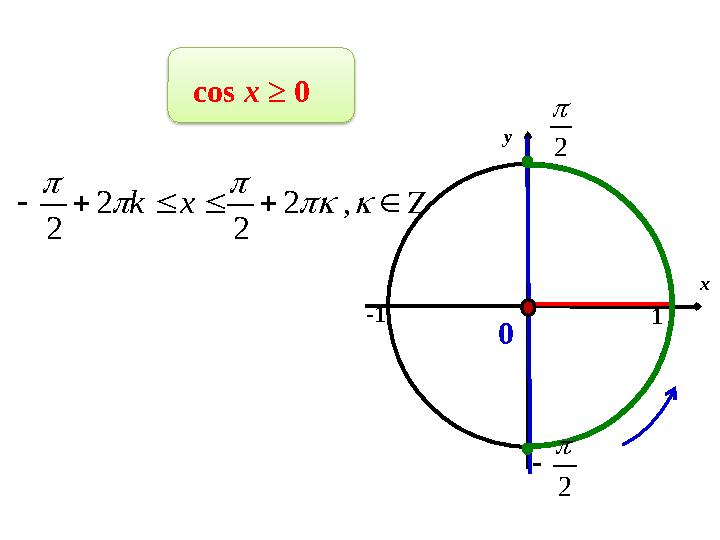
cos x ≥ 0 2  2        , 2 2 2 2 xk x y 1-1 0

18 слайд

cos x ≥ 0 2  2        , 2 2 2 2 xk x y 1-1 0

19 слайд
Мысалы: cosx > 2 1 теңсіздігін шешейік. Бір координаталық жүйеде теңсіздіктің оң және сол жақ бөліктерін, яғни y = cosx және y = 2 1 қатысты функциялардың графиктерін салайық. y = 2 1 түзуінің графигінен y = cosx функциясының графигі жоғары орналасқан бөліктерін аралықтармен белгілейік. 1. Аралықтардың бірінің ұштары болатын және , 32 1 arccos 1  x 32 1 arccos 2  x теңдіктері орындалатындай, y = cosx және y = 2 1 функцияларының графиктері қиылысқан нүктелерінің 1x және 2x абсциссаларын табайық. Косинус 2 периодты екенін ескерсек, теңсіздіктің жауабы ( 3  +2k; 3  +2k), k∈Z аралықтағы х -тің мәндері болады. 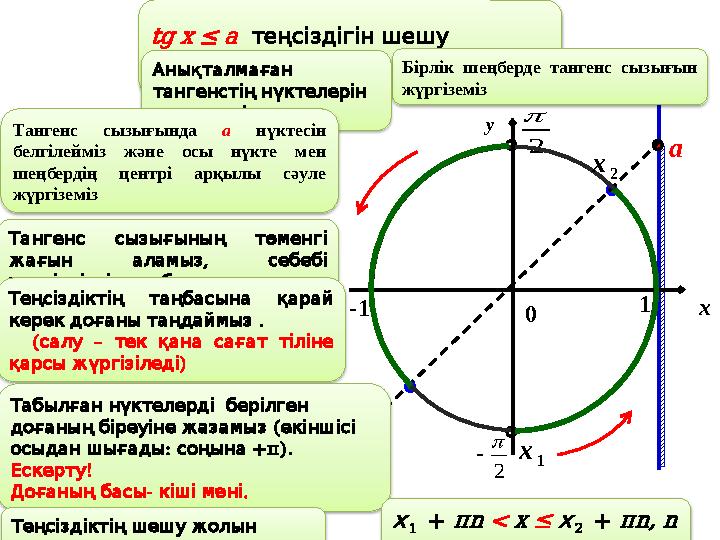Қарапайым тригонометриялық график көмегімен шешу.

19 слайд

Мысалы: cosx > 2 1 теңсіздігін шешейік. Бір координаталық жүйеде теңсіздіктің оң және сол жақ бөліктерін, яғни y = cosx және y = 2 1 қатысты функциялардың графиктерін салайық. y = 2 1 түзуінің графигінен y = cosx функциясының графигі жоғары орналасқан бөліктерін аралықтармен белгілейік. 1. Аралықтардың бірінің ұштары болатын және , 32 1 arccos 1  x 32 1 arccos 2  x теңдіктері орындалатындай, y = cosx және y = 2 1 функцияларының графиктері қиылысқан нүктелерінің 1x және 2x абсциссаларын табайық. Косинус 2 периодты екенін ескерсек, теңсіздіктің жауабы ( 3  +2k; 3  +2k), k∈Z аралықтағы х -тің мәндері болады. Қарапайым тригонометриялық график көмегімен шешу.

20 слайд
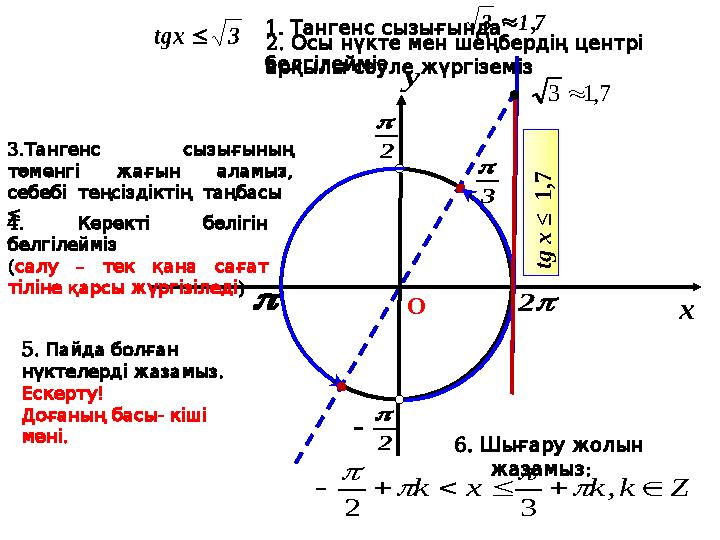
а2  2   -1 x y 1 0 tg x ≤ a теңсіздігін шешу алгоритмі Бірлік шеңберде тангенс сызығын жүргіземіз Анықталмаған тангенстің нүктелерін көрсетеміз Тангенс сызығында a нүктесін белгілейміз және осы нүкте мен шеңбердің центрі арқылы сәуле жүргіземіз Тангенс сызығының төменгі , жағын аламыз себебі теңсіздіктің таңбасы ≤ Теңсіздіктің таңбасына қарай . керек доғаны таңдаймыз ( – салу тек қана сағат тіліне ) қарсы жүргізіледі Табылған нүктелерді берілген ( доғаның біреуіне жазамыз екіншісі : осыдан шығады + соңына π). ! Ескерту - . Доғаның басы кіші мәні х 1 х 2 Теңсіздіктің шешу жолын жазамыз х 1 + πn < x ≤ х 2 + πn, n ϵ Z

20 слайд

а2  2   -1 x y 1 0 tg x ≤ a теңсіздігін шешу алгоритмі Бірлік шеңберде тангенс сызығын жүргіземіз Анықталмаған тангенстің нүктелерін көрсетеміз Тангенс сызығында a нүктесін белгілейміз және осы нүкте мен шеңбердің центрі арқылы сәуле жүргіземіз Тангенс сызығының төменгі , жағын аламыз себебі теңсіздіктің таңбасы ≤ Теңсіздіктің таңбасына қарай . керек доғаны таңдаймыз ( – салу тек қана сағат тіліне ) қарсы жүргізіледі Табылған нүктелерді берілген ( доғаның біреуіне жазамыз екіншісі : осыдан шығады + соңына π). ! Ескерту - . Доғаның басы кіші мәні х 1 х 2 Теңсіздіктің шешу жолын жазамыз х 1 + πn < x ≤ х 2 + πn, n ϵ Z

21 слайд
x y 2   2 7,13 2   3  Zkkxk  , 32     3tgx 1. Тангенс сызығында белгілейміз 7,13 3. Тангенс сызығының , төменгі жағын аламыз себебі теңсіздіктің таңбасы ≤ 4. Керекті бөлігін белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі ) 5. Пайда болған . нүктелерді жазамыз ! Ескерту - Доғаның басы кіші . мәні 2. Осы нүкте мен шеңбердің центрі арқылы сәуле жүргіземіз О t g x ≤ 1 , 7 6. Шығару жолын : жазамыз

21 слайд

x y 2   2 7,13 2   3  Zkkxk  , 32     3tgx 1. Тангенс сызығында белгілейміз 7,13 3. Тангенс сызығының , төменгі жағын аламыз себебі теңсіздіктің таңбасы ≤ 4. Керекті бөлігін белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі ) 5. Пайда болған . нүктелерді жазамыз ! Ескерту - Доғаның басы кіші . мәні 2. Осы нүкте мен шеңбердің центрі арқылы сәуле жүргіземіз О t g x ≤ 1 , 7 6. Шығару жолын : жазамыз

22 слайд
tg x ≤ 1 x 1 -1 Zkkkx  ], 4 ; 2 (     4  2  2   4 5 y 1 0

22 слайд

tg x ≤ 1 x 1 -1 Zkkkx  ], 4 ; 2 (     4  2  2   4 5 y 1 0

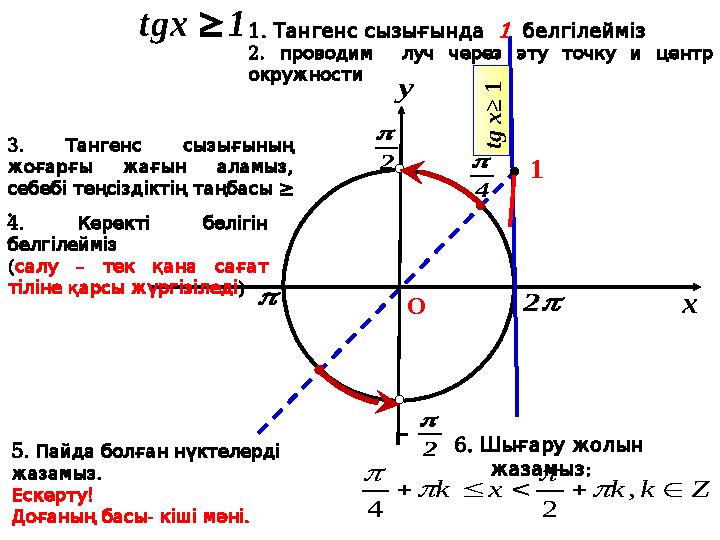
23 слайд
x y 2   2 2   4  Zkkxk  , 24     1tgx 1 2. проводим луч через эту точку и центр окружности О t g x ≥ 1 1. Тангенс сызығында 1 белгілейміз 3. Тангенс сызығының , жоғарғы жағын аламыз себебі теңсіздіктің таңбасы ≥ . 4. Керекті бөлігін белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі ) 5. Пайда болған нүктелерді . жазамыз ! Ескерту - . Доғаның басы кіші мәні 6. Шығару жолын : жазамыз

23 слайд

x y 2   2 2   4  Zkkxk  , 24     1tgx 1 2. проводим луч через эту точку и центр окружности О t g x ≥ 1 1. Тангенс сызығында 1 белгілейміз 3. Тангенс сызығының , жоғарғы жағын аламыз себебі теңсіздіктің таңбасы ≥ . 4. Керекті бөлігін белгілейміз ( – салу тек қана сағат тіліне қарсы жүргізіледі ) 5. Пайда болған нүктелерді . жазамыз ! Ескерту - . Доғаның басы кіші мәні 6. Шығару жолын : жазамыз

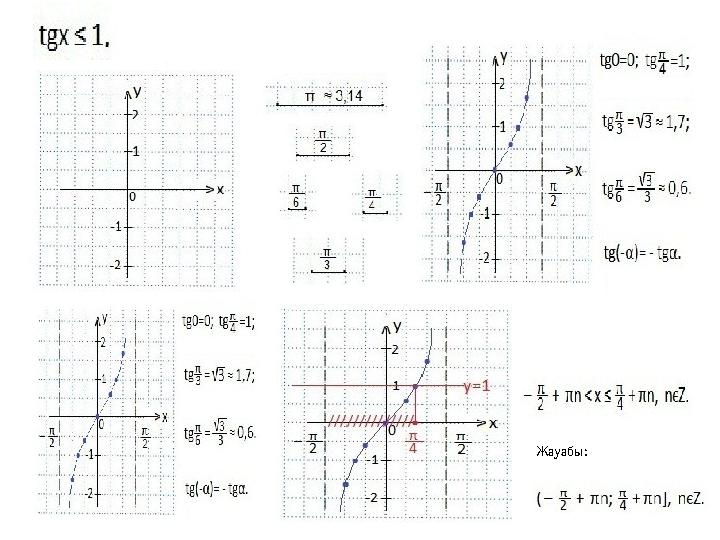
24 слайд
Жауабы:

24 слайд

Жауабы:

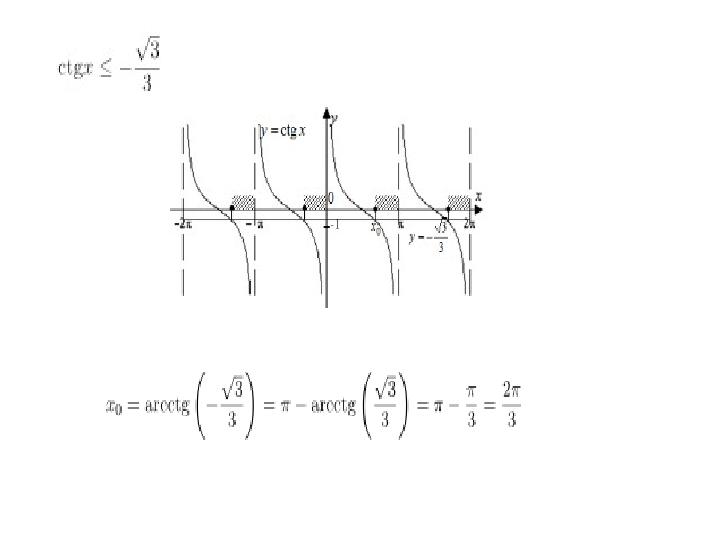
25 слайд

26 слайд
Формулалар! 1.sint<a (-1≤а≤1) ; — π — arcsin a + 2πn < t < arcsin a+2πn, nєZ. 2. sint>a ( -1≤a≤1); arcsin a + 2πn < t < π — arcsin a + 2πn, nєZ. 3. cost<a, (-1≤а≤1); arccos a + 2πn < t < 2π — arccos a + 2πn, nєZ. 4. cost>a, (-1≤а≤1); - arccos a + 2πn < t < arccos a + 2πn, nєZ. 5. tgt<a; — (π/2) + πn < t < arctg a + πn, где nєZ.

26 слайд

Формулалар! 1.sint<a (-1≤а≤1) ; — π — arcsin a + 2πn < t < arcsin a+2πn, nєZ. 2. sint>a ( -1≤a≤1); arcsin a + 2πn < t < π — arcsin a + 2πn, nєZ. 3. cost<a, (-1≤а≤1); arccos a + 2πn < t < 2π — arccos a + 2πn, nєZ. 4. cost>a, (-1≤а≤1); - arccos a + 2πn < t < arccos a + 2πn, nєZ. 5. tgt<a; — (π/2) + πn < t < arctg a + πn, где nєZ.

27 слайд
Пысықтауға арналған тапсырмалар https://bilimland.com/kk/subject/algebra/10-synyp/trigonometriyalyq-tengsi zdikterdi-sheshu?mid=033c1f02-9d5a-11e9-be78-49d30a05e051

27 слайд

Пысықтауға арналған тапсырмалар https://bilimland.com/kk/subject/algebra/10-synyp/trigonometriyalyq-tengsi zdikterdi-sheshu?mid=033c1f02-9d5a-11e9-be78-49d30a05e051

28 слайд
https://bilimland.com/kk/subject/algebra/10-synyp/trigonometriyalyq-tengsizdi kterdi-sheshu?mid=033c1f03-9d5a-11e9-be78-49d30a05e051 Сәйкесін тап!!!

28 слайд

https://bilimland.com/kk/subject/algebra/10-synyp/trigonometriyalyq-tengsizdi kterdi-sheshu?mid=033c1f03-9d5a-11e9-be78-49d30a05e051 Сәйкесін тап!!!

29 слайд
Өздігінен орындауға ұсынылатын тапсырмалар

29 слайд

Өздігінен орындауға ұсынылатын тапсырмалар

30 слайд

31 слайд
Рефлексия •Есіме түсті ……………………………….. •Қиындықтар туындады …………….. •Білгім келеді ………………………... •Қолымнан келді…………………………… •Қалап едім ………………………….

31 слайд

Рефлексия •Есіме түсті ……………………………….. •Қиындықтар туындады …………….. •Білгім келеді ………………………... •Қолымнан келді…………………………… •Қалап едім ………………………….