Материалдар / Туындының анықтамасы және оның геометриялық, физикалық мағынасы. Функцияның графигіне жүргізілген жанама. Туындының қолданылуы

Туындының анықтамасы және оның геометриялық, физикалық мағынасы. Функцияның графигіне жүргізілген жанама. Туындының қолданылуы

Материал туралы қысқаша түсінік

Математика пәнінің оқытушысы Жүргенова Күнзипаш Сарсенбайқызы

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

22 Маусым 2021

1247

4 рет жүктелген

Алгебра Ашық сабақ Басқа

770 ₸

Бүгін алсаңыз
+39 бонус беріледі
Бұл не?

Бүгін алсаңыз +39 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 29

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд
Математика Оқытушы: Жүргенова Күнзипаш Сарсенбайқызы

1 слайд

Математика Оқытушы: Жүргенова Күнзипаш Сарсенбайқызы

2 слайд
Туындының анықтамасы және оның геометриялық, физикалық мағынасы. Функцияның графигіне жүргізілген жанама. Туындының қолданылуы

2 слайд

3 слайд
Сабақ мақсаты: 1. Т уындының анықтамасы және туындыны табу ережелерін білу. 2.Туындының физикалық және геометриялық мағынасы. 3.Туындының қолданылуы. Функция графигіне жүргізілген жанаманың теңдеуі.

3 слайд

Сабақ мақсаты: 1. Т уындының анықтамасы және туындыны табу ережелерін білу. 2.Туындының физикалық және геометриялық мағынасы. 3.Туындының қолданылуы. Функция графигіне жүргізілген жанаманың теңдеуі.

4 слайд
Білімділік: оқушыларға туынды табу ережесін меңгерту, функцияның графигіне жүргізілген жанаманың теңдеуін меңгерту, есептер шығару барысында туынды анықтамасының формуласын қолдануға дағдыландыру және есептің шешімін тексеріп,дұрыстығына көз жеткізе алуы;

4 слайд

Білімділік: оқушыларға туынды табу ережесін меңгерту, функцияның графигіне жүргізілген жанаманың теңдеуін меңгерту, есептер шығару барысында туынды анықтамасының формуласын қолдануға дағдыландыру және есептің шешімін тексеріп,дұрыстығына көз жеткізе алуы;

5 слайд
Дамытушылық: логикалық ойлау қабілетін дамыту, математикалық сауаттылығын арттыру; Тәрбиелік: өз бетімен және топпен жұмыстануға және ізденуге үйрету, жауапкершілікке, ұқыптылыққа тәрбиелеу.

5 слайд

Дамытушылық: логикалық ойлау қабілетін дамыту, математикалық сауаттылығын арттыру; Тәрбиелік: өз бетімен және топпен жұмыстануға және ізденуге үйрету, жауапкершілікке, ұқыптылыққа тәрбиелеу.

6 слайд
) ( ) ( ) ( lim lim 0 0 x f x x f x x f x y x x              , ) ( 1 /      x x C’= 0 Х ''=1 (ах)’=а

6 слайд

) ( ) ( ) ( lim lim 0 0 x f x x f x x f x y x x              , ) ( 1 /      x x C’= 0 Х ''=1 (ах)’=а

7 слайд
1.Туынды дегеніміз y=f(x) функциясының х -тің xₒ - ге ұмтылғандағы шегі xₒ нүктедегі функция туындысы деп аталады, f ʹ(x) белгіленеді : 2)Физикалық мағанасы: y=f(x) функциясының х нүктедегі f ʹ(x) туындысы х нүктесін дегі өзгеру жылдамдығын анықтайды sʹ(t)=v(t) — қозғалысағы дененің t уақыт мезетіндегі лездік жылдамдығы; vʹ(t)= а (х) — жылдамдықтан алынған туынды удеуге тең.

7 слайд

1.Туынды дегеніміз y=f(x) функциясының х -тің xₒ - ге ұмтылғандағы шегі xₒ нүктедегі функция туындысы деп аталады, f ʹ(x) белгіленеді : 2)Физикалық мағанасы: y=f(x) функциясының х нүктедегі f ʹ(x) туындысы х нүктесін дегі өзгеру жылдамдығын анықтайды sʹ(t)=v(t) — қозғалысағы дененің t уақыт мезетіндегі лездік жылдамдығы; vʹ(t)= а (х) — жылдамдықтан алынған туынды удеуге тең.

8 слайд
3 ) Геометриялық мағанасы: y=f( х) функциясының xₒ нүктесіндегі туындысы f ʹ( х ₒ) осы функция графигінің ( xₒ;f(xₒ)) нүктесі арқылы өтетін жанамасының бұрыштық коэфициентіне тең: f ʹ( х ₒ)=tg α= k.

8 слайд

3 ) Геометриялық мағанасы: y=f( х) функциясының xₒ нүктесіндегі туындысы f ʹ( х ₒ) осы функция графигінің ( xₒ;f(xₒ)) нүктесі арқылы өтетін жанамасының бұрыштық коэфициентіне тең: f ʹ( х ₒ)=tg α= k.

9 слайд
y = f(x) функциясы Nₒ(xₒ;yₒ) нүктесінде f ʹ(xₒ) бар болсын . Жанаманың теңдеуі түзу болғандықтан y =kx + b сызықтық функция ретінде іздейміз .

9 слайд

y = f(x) функциясы Nₒ(xₒ;yₒ) нүктесінде f ʹ(xₒ) бар болсын . Жанаманың теңдеуі түзу болғандықтан y =kx + b сызықтық функция ретінде іздейміз .

10 слайд
y=kx+b түзу теңдеуі бойынша мұндағы k=tgα= f ʹ(xₒ), бұдан y= f ʹ(xₒ) x+b.

10 слайд

y=kx+b түзу теңдеуі бойынша мұндағы k=tgα= f ʹ(xₒ), бұдан y= f ʹ(xₒ) x+b.

11 слайд
Nₒ(xₒ;f (xₒ) ) нүктесінің координаталары бойынша f (xₒ)= f ʹ(xₒ) xₒ+b f (xₒ)= f ʹ(xₒ) xₒ+b теңдеуінен b-ны табамыз: b = f (xₒ)- f ʹ(xₒ) xₒ b = f (xₒ)- f ʹ(xₒ) xₒ теңдеуін y= f ʹ(xₒ) x+b теңдеуіне қоямыз: y= f ʹ(xₒ) x+ f (xₒ)- f ʹ(xₒ) xₒ.

11 слайд

Nₒ(xₒ;f (xₒ) ) нүктесінің координаталары бойынша f (xₒ)= f ʹ(xₒ) xₒ+b f (xₒ)= f ʹ(xₒ) xₒ+b теңдеуінен b-ны табамыз: b = f (xₒ)- f ʹ(xₒ) xₒ b = f (xₒ)- f ʹ(xₒ) xₒ теңдеуін y= f ʹ(xₒ) x+b теңдеуіне қоямыз: y= f ʹ(xₒ) x+ f (xₒ)- f ʹ(xₒ) xₒ.

12 слайд
y= f (xₒ)- f ʹ(xₒ) (х- xₒ) жанама теңдеуі. ЖАНАМАНЫҢ ТЕҢДЕУІН ЖАЗУ АЛГОРИТМІ • xₒ -ге сәйкес f (xₒ)— ді есептеу . • f (x) функциясының туындысын табу. • xₒ— дегі туындының мәні f ʹ(xₒ)— ді есептеу. • y= f (xₒ)+ f ʹ(xₒ) ·(x — xₒ) формуласына қойып жанаманың теңдеуін алу.

12 слайд

y= f (xₒ)- f ʹ(xₒ) (х- xₒ) жанама теңдеуі. ЖАНАМАНЫҢ ТЕҢДЕУІН ЖАЗУ АЛГОРИТМІ • xₒ -ге сәйкес f (xₒ)— ді есептеу . • f (x) функциясының туындысын табу. • xₒ— дегі туындының мәні f ʹ(xₒ)— ді есептеу. • y= f (xₒ)+ f ʹ(xₒ) ·(x — xₒ) формуласына қойып жанаманың теңдеуін алу.

13 слайд
Сабақты бекіту есептері: 1 - мысал. y=x² параболасына (1;1) нүктесінде жүргізілген жанаманың бұрыштық коэффициентін табыңыз және жанама теңдеуін жаз Шешуі: f(x)=x² функциясынан: f( 1 )= 1 ² = 1 f ʹ(x)=2 х f ʹ( 1 )=f ʹ(1)=2·1=2 k = f ʹ(1)=tg α=2 у=1+2(х-1)=1+2х-2 у = 2х -1 y =kx + b

13 слайд

Сабақты бекіту есептері: 1 - мысал. y=x² параболасына (1;1) нүктесінде жүргізілген жанаманың бұрыштық коэффициентін табыңыз және жанама теңдеуін жаз Шешуі: f(x)=x² функциясынан: f( 1 )= 1 ² = 1 f ʹ(x)=2 х f ʹ( 1 )=f ʹ(1)=2·1=2 k = f ʹ(1)=tg α=2 у=1+2(х-1)=1+2х-2 у = 2х -1 y =kx + b

14 слайд
2-мысал: f (x)=x²-5x+6 функциясының xₒ=1 нүктесіндегі жанаманың теңдеуін жазыңыз. • f (xₒ) =f(1)=1²-5·1+6=2. • f ʹ(x)=2x-5. • f ʹ(xₒ)= f ʹ(1)=2·1-5=-3 • y= f (xₒ)+ f ʹ(xₒ) ·(x — xₒ) =2-3(x-1)=2-3x+3=5-3x. Бұдан жанаманың теңдеуі: y=5-3x y =kx + b

14 слайд

2-мысал: f (x)=x²-5x+6 функциясының xₒ=1 нүктесіндегі жанаманың теңдеуін жазыңыз. • f (xₒ) =f(1)=1²-5·1+6=2. • f ʹ(x)=2x-5. • f ʹ(xₒ)= f ʹ(1)=2·1-5=-3 • y= f (xₒ)+ f ʹ(xₒ) ·(x — xₒ) =2-3(x-1)=2-3x+3=5-3x. Бұдан жанаманың теңдеуі: y=5-3x y =kx + b

15 слайд
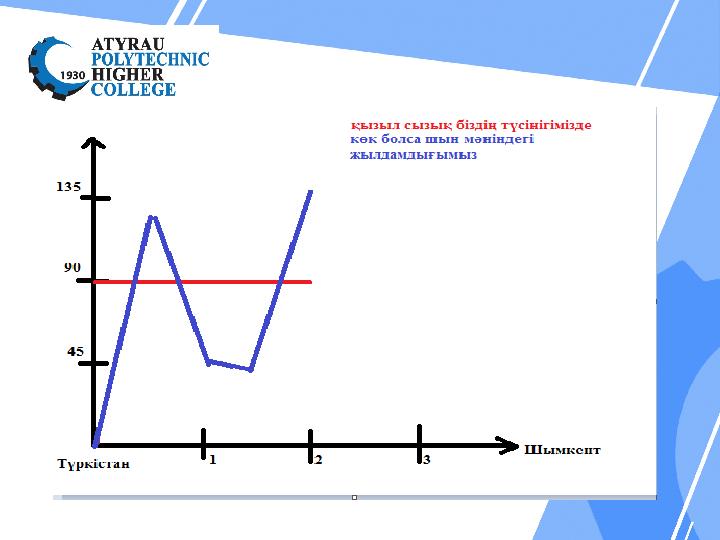
Мысалға көлікті алайық

15 слайд

Мысалға көлікті алайық

16 слайд

17 слайд
Өндірісте қолданылатын техникалық құрал жабдықтарды жасау,жөндеу және пайдалану мерзімдерінің ұзақтығы анықтауға туынды есептерінің көмегіне жүгінеді. Мысалы МКиПИА -18 тобындағы мамандыққа баулитын сабақтардың бірі Өлшеу, бақылау құралдарын жөндеу және техникалық қызмет көрсету

17 слайд

Өндірісте қолданылатын техникалық құрал жабдықтарды жасау,жөндеу және пайдалану мерзімдерінің ұзақтығы анықтауға туынды есептерінің көмегіне жүгінеді. Мысалы МКиПИА -18 тобындағы мамандыққа баулитын сабақтардың бірі Өлшеу, бақылау құралдарын жөндеу және техникалық қызмет көрсету

18 слайд

19 слайд

20 слайд

21 слайд
f ( x )=−3 x 2 +5 x −5 f ( x )=5 x 3 −3 x 2 +2 x

21 слайд

f ( x )=−3 x 2 +5 x −5 f ( x )=5 x 3 −3 x 2 +2 x

22 слайд

23 слайд
Бақылау сұрақтары мен тапсырмалары: • f (x)=x²-10x+6 функциясының xₒ=4 нүктесіндегі жанаманың теңдеуін жазыңыз. • f (x)=12-3x+2x² функциясының xₒ=2,5 нүктесіндегі жанаманың теңдеуін жаз. • f(x)=x²-3x+5 M(0;5) нүктесі арқылы өтетін жанамасының бұрыштық коэффициентін табыңыз. • b- ның қандай мәнінде y=-10x+b түзуі f(x)=3x²-4x+2 функциясының грaфигіне жанама болады. • b- ның қандай мәнінде y=8x+b түзуі f(x)=x²+2x³ функциясының грaфигіне жанама болады.

23 слайд

Бақылау сұрақтары мен тапсырмалары: • f (x)=x²-10x+6 функциясының xₒ=4 нүктесіндегі жанаманың теңдеуін жазыңыз. • f (x)=12-3x+2x² функциясының xₒ=2,5 нүктесіндегі жанаманың теңдеуін жаз. • f(x)=x²-3x+5 M(0;5) нүктесі арқылы өтетін жанамасының бұрыштық коэффициентін табыңыз. • b- ның қандай мәнінде y=-10x+b түзуі f(x)=3x²-4x+2 функциясының грaфигіне жанама болады. • b- ның қандай мәнінде y=8x+b түзуі f(x)=x²+2x³ функциясының грaфигіне жанама болады.

24 слайд
= f ( x )= x 4 −7 x +2 f ( x )=− x 2 +4 x +1 f ( x )=4 x 2 −2 x +1 f ( x )=− x 4 +2 x 3 +1Тест-есептер Әр бір функцияны бірінші координатасы 1 болатын P нүктесінде жүргізілген жанамасының теңдеуі н табыңыздар:

24 слайд

= f ( x )= x 4 −7 x +2 f ( x )=− x 2 +4 x +1 f ( x )=4 x 2 −2 x +1 f ( x )=− x 4 +2 x 3 +1Тест-есептер Әр бір функцияны бірінші координатасы 1 болатын P нүктесінде жүргізілген жанамасының теңдеуі н табыңыздар:

25 слайд
Бекіту: Сұрақтар, есептер тест тапсырмасы Бағалау критерийі: 9-10 ұпай жинағандар ---80-90% 6-8 жақсы -------------------70-79% 3-5 қанағаттанарлық---50-69%

25 слайд

Бекіту: Сұрақтар, есептер тест тапсырмасы Бағалау критерийі: 9-10 ұпай жинағандар ---80-90% 6-8 жақсы -------------------70-79% 3-5 қанағаттанарлық---50-69%

26 слайд
Рефлексия

26 слайд

Рефлексия

27 слайд
Назарла рыңызға рахмет!

27 слайд

Назарла рыңызға рахмет!

28 слайд