ҰБТ-ге дайындауда математика пәнінен есеп шығарудың тиімді әдістерің таңдау

1 слайд
Батыс Қазақстан облысы Ақжайық ауданы Тайпақ орта жалпы білім беретін мектебі ҰБТ-ге дайындауда математика пәнінен есеп шығарудың тиімді әдістерін таңдау Есмуханова Қ.Қ. жоғарғы санатты математика пәні мұғалімі 16 мамыр,2016 жыл.

1 слайд

2 слайд
Мектеп тәжірибесінде оқушыларды математикадан ҰБТ-ға дайындау кезінде уақытты тиімді пайдалана білу мәселесіне жеткілікті дәрежеде көңіл бөлінбейтіндігі айтылып жүр. Жалпы алғанда барлығы 3 сағат,сонда әрбір тест сұрағына жауап беруге орта есеппен 1,5 минут қана уақыт бөлу керек. Ал енді осы 1,5 минут ішінде кейбір күрделі математика есептерін орындап үлгеру мүмкін бе? ҰБТ-да математикадан жоғары нәтиже көрсетудің бірден бір ,аса қажетті шарттары: 1.Тиянақты,әрі терең математикалық біліммен қарулану 2.Белгілі бір есепті шешудің өзіндік математикалық әдісі мен жолын білу 3.Психологиялық дайындықтың болуы: мектеп тәжірибесінен алсақ 3 жыл қатар ортадан жоғары денгейде оқитын балалар екілік алды ,бірақ әртүрлі оқу орнының грант иегері болды, бір оқушы БҚАТУ–не грантқа түсіп, аяқтап шықты. Есте сақтайтын жағдай оқушы әзірлік кезінде қай пәнге қанша уақыт жіберетінін есептеп,дағдылануы,яғни қалыптасуы қажет

2 слайд

3 слайд
Кейбір тест тапсырмаларын орындаудың әркім біле бермейтін аса қарапайым және оңай әдістері,толып жатқан тест технологиялары бар. Сондықтан оқушының математикалық білімдерін тереңдету мәселесімен ғана шектелмей,оны осы технологияларды меңгеруге және оларды ҰБТ кезінде тиімді пайдалана білуге үйретуіміз қажет деп есептеймін. Олар: логикалық ойлау негізінде тест тез орындау әдістері ,жауаптарды бағалау әдісі,симметрия әдісі т.б. Мысал: А) y=18x b)y=12x-1 c)y=5x-13 d) y=19x-11 e)7x+10 Шарт бойынша жанама да берілген функция да абциссасы нүктесінен өтеді. Сондықтан, f(1)=8 тексереміз: а) b)8 12*1-1 c)8 5*1-13 d)8=19*1-11 e)8 7*1+10 Жауабы: д)

3 слайд

4 слайд
Мысал: теңсіздікті шеш : a) b) c) d)(- Жауаптарды бағалау әдісін қолдансақ: берілген теңсіздікке А),Е) жауаптарына енбейтін х =1 санын қойсақ: демек x=1 теңсіздікті қанағаттандырады, демек ол енбейтін А),Е) жауаптарын сызып тастаймыз. Сонда ол енетін В),С),Д) –ның бірі дұрыс болуы тиіс,енді теңсіздікке x=0 санын қоямыз: сонда Ал ,0 саны С) жауабына тиісті,сондықтан С) сызып тастаймыз,Қалған 2 жауаптың қайсысы дұрыс екенін анықтау үшін x= 2 деп алу тиімді. сонда Олай болса, 2 саны еніп тұрған Д) жауабы дұрыс емес,ендеше ,қалған В) жауабы дұрыс . Жауабы: b) Теңдеуді шеш: A) -9 b)16 C)21 d) 9 e)19 Жауаптарға қарай отырып, шешімі оң сан және бүтін және квадрат түбір дәл табылатын сан болатындығын байқау оңай. Сондықтан, а,с,е жауаптарын сызып тастаймыз. В және д жауаптарын қойып тексереміз Жауап: д) Теңдеуді шеш:/ 2014,№0013.10/ - a) шешімі жоқ в)-1 с)2,5 д)1,5 е)1 Жауаптарға қарасақ а,с,д сызып тастауға болады, в мен е орнына қойып тексер c ек, жауабы е)

4 слайд

5 слайд
№ 0 013 .13.2014 ж. теңсіздіктер жүйесін шешу: 1. тармағы жоғары қараған парабола, ох осімен (-3;0) және (3;0) нүктесінде қиылысады. Шешімі: (-3;3) 2 . тармағы жоғары қараған парабола, ох осімен (0;0) және (-2;0) нүктесінде қиылысады. Шешімі: (-) 3 .Ортақ шешім: № 0 013 .13.2014 ж. 4- ке еселік барлық екі таңбалы сандардың қосындысын тап 4-ке еселік екі таңбалы сандар тізбегі: 12,16,20,,,,,96 Тізбек арифметикалық прогрессия

5 слайд

6 слайд
Тригонометриялық теңсіздіктерді графиктік тәсіл, бірлік шеңберді қолдану, формуланы қолдану тәсілдері арқылы шешуге болады. Sinx>a |a|<1 Sin x<a |a|<1 cosx>a | a|<1 cosx<a |a|<1 tgx>a tg x<a ctgx>a ctgx<a

6 слайд

7 слайд
Оқушылар модулмен берілген есептерді шығаруда қиналып жатады: - sinx , соңғы теңдеуден шығатыны : Сол жағында модуль болғандықтан - sinx(sinx+1) , - *sinx cosx=-1, x= n,n

7 слайд

8 слайд
№ 0 013 .22.2014 ж. Теңсіздікті шеш: *cos> - 2* *cos> - *2 , - arcsin(- - -arcsin(- - )+2 - + - + - + n,n Тригонометриялық теңдеулер мен теңсіздіктерді шешуде: 0001- нұсқа,№ 22 5cosx+cos2x+3 , cosx=t, 2 1. t, cosx x 2. t cosx

8 слайд

9 слайд
І ұүйма   ІІ құйма   қорытынды мыс қорғасын + мыс қорғас ын = мыс Қорғас ын 15%   65%   30%   Хг   Уг   200 гmc mb ma ma   1 0, % 100* mc mb ma 100%* ma      C Ca Vc Vb Va Va   % 100* Vc Vb Va 100%* Va aC   m P m m C m a a a a * ; *  Ерітінділер,құймаларға берілген есептер: Құймалар /қатты,сұйық,газ,сусымалы т.б./ А,В,С құрамдарынан тұрсын,олардың массалары сәйкесінше m a,, m b, m c болады. Сонда барлық құйманың массасы m=m a, +m b +m c болады. А құрамының осы құймадағы үлесін С а деп белгілесек C a = Ал, пайыздық үлесі Р a = С=0 болса,құймада А құрамы жоқ. С = 1 болса,құйма А құрамынан тұрады /В,С құрамдары үшінде осылай болады. V көлемі бойынша заттың үлесі дәл осылай табылады. С = ,ал пайыздық үлесі P a = C a немесе Р а белгілі болса,А құраушы заттың мөлщері Осындай типті есептерді шығарғанда жеңілдік үшін мынадай схеманы пайдаланған қолайлы: құйманы төртбұрыш ретінде сызып,енетін құрамдары бойынша төртбұрышты бөліктерге бөліп,ол бөліктердің ішіне құрамның үлесін жазамыз, егер құймаларды біріктірсе ,яғни бірге балқытса,біріктіріп араластырса онда төртбұрыштар арасына « + » ,егер құймаларды ажыратса , яғни буланса,кептірсе, онда төртбұрыштар арасына « - « таңбасын жазамыз. Мысал: Мыс пен қорғасыннан тұратын екі құйма бар. Бір құймада мыс мөлшері 15 %,екіншісінде 65% болса,құрамында 30%мыс болатын 200 г құйма шығу үшін әр құймадан қанша алып,біріктіріп балқыту керек? І құйманың массасы-Х г болса,мұндағы мыс мөлшері 0,15 г ІІ құйманың массасы-У г болса, мұндағы мыс мөлшері 0,65 г Жаңа құймадағы мыс мөлшері 0,3*200 =0.6 г Теңдеу: 0,15*X+0,65*Y=0,3*200 Жауабы:140 г,60г

9 слайд

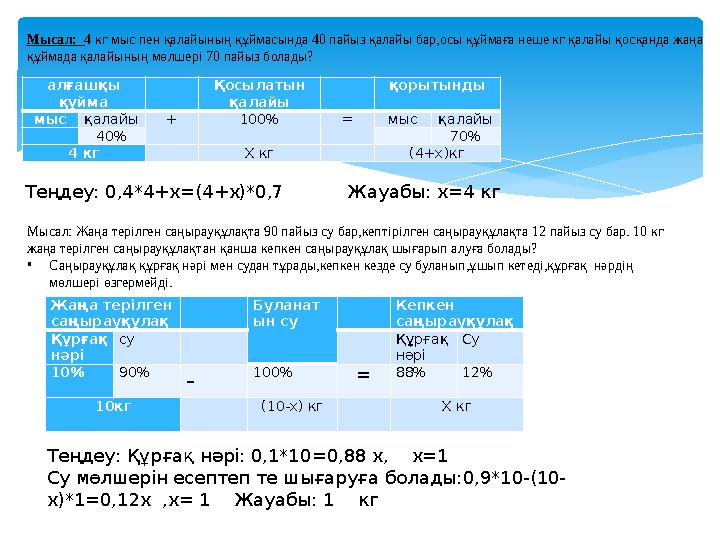
10 слайд
Мысал: 4 кг мыс пен қалайының құймасында 40 пайыз қалайы бар,осы құймаға неше кг қалайы қосқанда жаңа құймада қалайының мөлшері 70 пайыз болады? алғашқы құйма   Қосылатын қалайы   қорытынды мыс қалайы + 100% = мыс қалайы   40%   7 0% 4 кг   Х кг   (4+х)кг Теңдеу: 0,4*4+x=(4+x)*0,7 Жауабы: х =4 кг Мысал: Жаңа терілген саңырауқұлақта 90 пайыз су бар,кептірілген саңырауқұлақта 12 пайыз су бар. 10 кг жаңа терілген саңырауқұлақтан қанша кепкен саңырауқұлақ шығарып алуға болады? • Саңырауқұлақ құрғақ нәрі мен судан тұрады,кепкен кезде су буланып,ұшып кетеді,құрғақ нәрдің мөлшері өзгермейді. Жаңа терілген саңырауқұлақ   Буланат ын су   Кепкен саңырауқұлақ Құрғақ нәрі су     Құрғақ нәрі Су 10% 90% - 100% = 88% 12% 10кг   (10-х) кг   Х кг Теңдеу: Құрғақ нәрі: 0,1*10 =0,88 x, x=1 Су мөлшерін есептеп те шығаруға болады: 0,9*10-(10- x)*1=0,12x ,x= 1 Жауабы: 1 кг

10 слайд

11 слайд
2014 ж. тест материалдарында логикалық есептер көптеп берілген. Соларды шығарудың жеңіл әрі шапшаң тәсілдерін таңдасақ: 0002 нұсқа,№2 Ұлы 10 жаста ,ал әкесі 58 жаста .Неше жылдан кейін ұлының жасы әкесінің жасынан 4 есе кіші болады? А)4 в)5 С) 8 Д) 6 Е)7 • Есепті теңдеу құрып шығаруға да болады, логикалық ойлапта шығаруға болады • 4*(10+x)=58+x, x=6 Жауабы: 6 0013-нұсқа,№25 Құмыра = шөлмек+бокал 2 құмыра = 7 бокал Шөлмек = кесе+2 бокал Шөлмек = ? Кесе Шешуі: 1. Қ = к+2 б+б =3 б+к 2. 2(3б+к) = 7 б, б = 2к 3.Ш = к+4к = 5 к Жауабы: 5 кесе Әкесі 11 12 13 14 15 16 Баласы 59 60 61 62 63 64

11 слайд

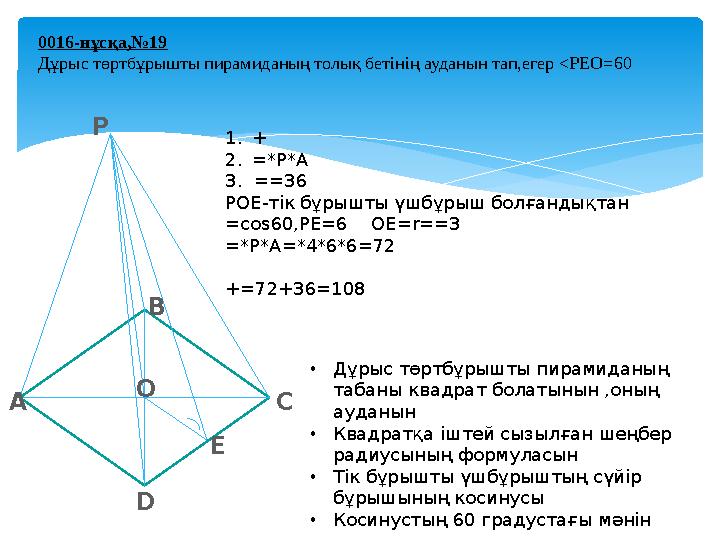
12 слайд
0016-нұсқа,№19 Дұрыс төртбұрышты пирамиданың толық бетінің ауданын тап,егер <PEO=60 1. + 2. =*P*A 3. ==36 РОЕ-тік бұрышты үшбұрыш болғандықтан =cos60,PE=6 OE=r==3 =*P*A=*4*6*6=72 +=72+36=108 • Дұрыс төртбұрышты пирамиданың табаны квадрат болатынын ,оның ауданын • Квадратқа іштей сызылған шеңбер радиусының формуласын • Тік бұрышты үшбұрыштың сүйір бұрышының косинусы • Косинустың 60 градустағы мәнін А P D C EB O

12 слайд

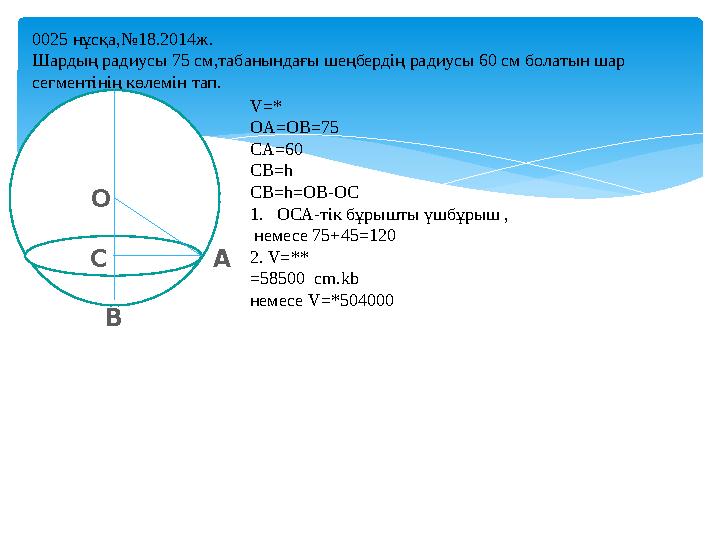
13 слайд
0025 нұсқа,№18.2014ж. Шардың радиусы 75 см,табанындағы шеңбердің радиусы 60 см болатын шар сегментінің көлемін тап. О В АС V=* OA=OB=75 CA=60 CB=h CB=h=OB-OC 1. ОСА-тік бұрышты үшбұрыш , немесе 75+45 =120 2. V=** =58500 cm.kb немесе V=*504000

13 слайд

14 слайд
0025 нұсқа,№24.2014 ж қабырғалары 15 см,15 см,24 см үшбұрышқа іштей сызылған шеңбер радиусын тап? • Үшбұрыш тең бүйірлі болғандықтан табанына түсірілген биіктік,медиана, биссектрисасы бір түзудің бойында болғандықтан ,биіктігі тең екі үшбұрышқа бөледі,сондықтан 1. биіктігін тауып алу: 2. бір тік бұрышты үшбұрыштың ауданы : S= 56 cm.kb 3. S=2*56=108 cm.kb 4. r==4 cm 0025 нұсқа,№13.2014 ж теңдеулер жүйесін шешу: a)(1;1) b)(-1;3) c) (4;-2) d) (3;1) e) (2;0) 1- ші теңдеуден х+у =2 болғандықтан d) жауабын бірден сызып тастаймыз, қалған жауаптарын ауызша тексереміз, жауабы: е) (2;0) 00 19- нұсқа,№12.2014 ж теңдеуді шеш: A) -1;-0,5 b)-2,5;2 c) 0,5;1 d)-1;0,5 e) -0,5;1 Анықталу облысын тапсақ: сонда а),е) жауаптарын сызып тастауға болады. Ортақ бөлімге келтіріп,теңдеуді шешсек : x=-1,x=0,5, яғни Д) жауабы.

14 слайд

15 слайд
Сызы қтық функциялардың модулдерінің қосындысының ең кіші мәні туралы теореманың қолданылуы : Y= болса,онда: 1. n жұп болса, болғанда ,y - ең кіші мәнді қабылдайды , яғни + + +….+ 2. n тақ болса, болғанда ,y - ең кіші мәнді қабылдайды , яғни + + +….+ Мысалы: =1, =2,=3,…,=23 болады, n=23 тақ сан болғандықтан =12 болғанда , Мұндағы: арифметикалық прогрессияның алғашқы n мүшесінің қосындысы : Мысалы: =475 948+946+….+2=225150 Мысалы: : ++…+=6451600

15 слайд

16 слайд

16 слайд