Материалдар / Вектор. Векторларға амалдар қолдану. Коллинеар және коллинеар емес векторлар

Вектор. Векторларға амалдар қолдану. Коллинеар және коллинеар емес векторлар

Материал туралы қысқаша түсінік

100% дайын слайд. Вектор. Векторларға амалдар қолдану. Коллинеар және коллинеар емес векторлар 9.1.4.1 вектордың, коллинеар векторлардың, тең векторлардың, нөлдік вектордың, бірлік вектордың және вектор ұзындығының анықтамаларын білу; 9.1.4.2 векторларды қосу, векторды санға көбейту ережелерін білу және қолдану; 9.1.4.3 векторлардың коллинеарлық шартын қолдану; 9.1.4.5 екі вектордың арасындағы бұрыштың анықтамасын білу;

Умарбеков Абдуллах Даниярович

Автор материалды ақылы түрде жариялады. Сатылымнан түскен қаражат авторға автоматты түрде аударылады. Толығырақ

10 Қырқүйек 2024

325

0 рет жүктелген

Геометрия Барлық материалдар 9 сынып

900 ₸

Бүгін алсаңыз
+45 бонус беріледі
Бұл не?

Бүгін алсаңыз +45 бонус беріледі Бұл не?

Тегін турнир Мұғалімдер мен Тәрбиешілерге
Дипломдар мен сертификаттарды алып үлгеріңіз!

Бұл бетте материалдың қысқаша нұсқасы ұсынылған. Материалдың толық нұсқасын жүктеп алып, көруге болады

1 / 37

Ресми байқаулар тізімі

Республикалық байқауларға қатысып жарамды дипломдар алып санатыңызды көтеріңіз!

Материалдың қысқаша түсінігі

1 слайд

2 слайд
Вектор ұғымы 9.3.4.1 вектордың, нөлдік вектордың, бірлік вектордың, коллинеар векторлардың, тең және қарама-қарсы векторлардың, векторлар арасындағы бұрыштың анықтамаларын біледі; 9.3.4.2 коллинеар, тең, қарама-қарсы векторларды және векторлар арасындағы бұрышты салуды біледі және суреті бойынша табады.

2 слайд

Вектор ұғымы 9.3.4.1 вектордың, нөлдік вектордың, бірлік вектордың, коллинеар векторлардың, тең және қарама-қарсы векторлардың, векторлар арасындағы бұрыштың анықтамаларын біледі; 9.3.4.2 коллинеар, тең, қарама-қарсы векторларды және векторлар арасындағы бұрышты салуды біледі және суреті бойынша табады.

3 слайд
Біздерге екі түрлі шамалар белгілі. Мысалы, ұзындық, аудан, көлем, масса және т. с. с шамалар (белгілі өлшем бірліктерінде) өздерінің сан мәндерімен толық анықталады. Мұндай шамаларды скалярлық шамалар немесе жай ғана скаляр деп атаймыз. Тек сандық мәндерімен ғана анықталатын шамаларды скаляр шамалар деп атайды.

3 слайд

Біздерге екі түрлі шамалар белгілі. Мысалы, ұзындық, аудан, көлем, масса және т. с. с шамалар (белгілі өлшем бірліктерінде) өздерінің сан мәндерімен толық анықталады. Мұндай шамаларды скалярлық шамалар немесе жай ғана скаляр деп атаймыз. Тек сандық мәндерімен ғана анықталатын шамаларды скаляр шамалар деп атайды.

4 слайд
Ал, көптеген физикалық шамалар, мысалы, күш, материалдық дененің қозғалысы, жылдамдығы және т. с. с шамалар тек өзінің сан мәндерімен ғана емес, кеңістіктегі бағыттарымен де сипатталады. Мұндай шамаларды векторлық шамалар немесе жай ғана вектор деп атайды. v

4 слайд

Ал, көптеген физикалық шамалар, мысалы, күш, материалдық дененің қозғалысы, жылдамдығы және т. с. с шамалар тек өзінің сан мәндерімен ғана емес, кеңістіктегі бағыттарымен де сипатталады. Мұндай шамаларды векторлық шамалар немесе жай ғана вектор деп атайды. v

5 слайд
Мысалы, қандай да бір денеге белгілі бір күшпен әсер ететін болсақ, онда физика курсында бұл күшті «бағытталған кесіндімен» бейнелейді. F

5 слайд

Мысалы, қандай да бір денеге белгілі бір күшпен әсер ететін болсақ, онда физика курсында бұл күшті «бағытталған кесіндімен» бейнелейді. F

6 слайд
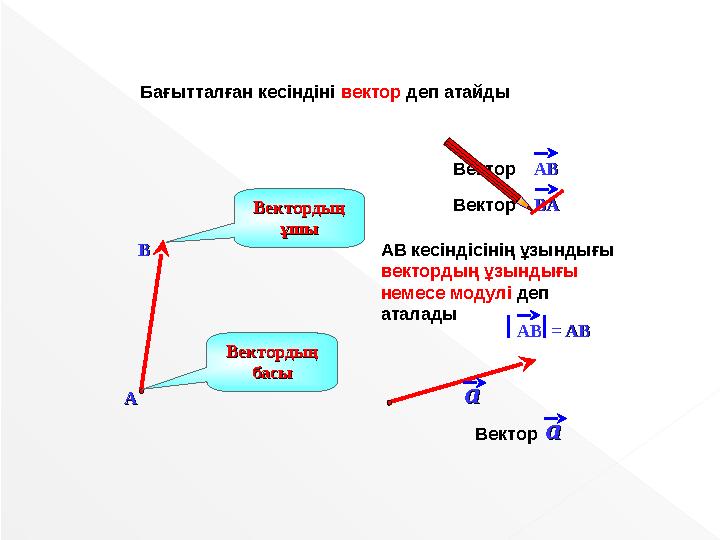
АВ кесіндісінің ұзындығы вектордың ұзындығы немесе модулі деп аталады ВАВАВектор Бағытталған кесіндіні вектор деп атайды АА ВВ aa АВАВ = = АВАВ Вектордың Вектордың басыбасы Вектордың Вектордың ұшыұшы АВАВВектор aaВектор

6 слайд

АВ кесіндісінің ұзындығы вектордың ұзындығы немесе модулі деп аталады ВАВАВектор Бағытталған кесіндіні вектор деп атайды АА ВВ aa АВАВ = = АВАВ Вектордың Вектордың басыбасы Вектордың Вектордың ұшыұшы АВАВВектор aaВектор

7 слайд
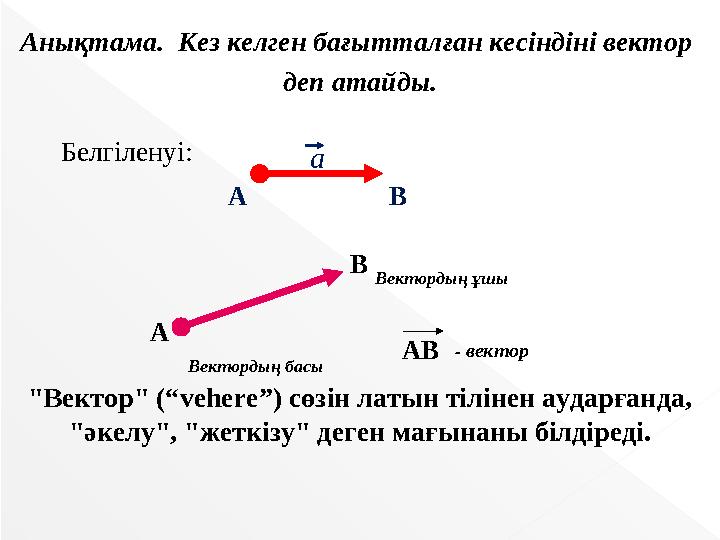
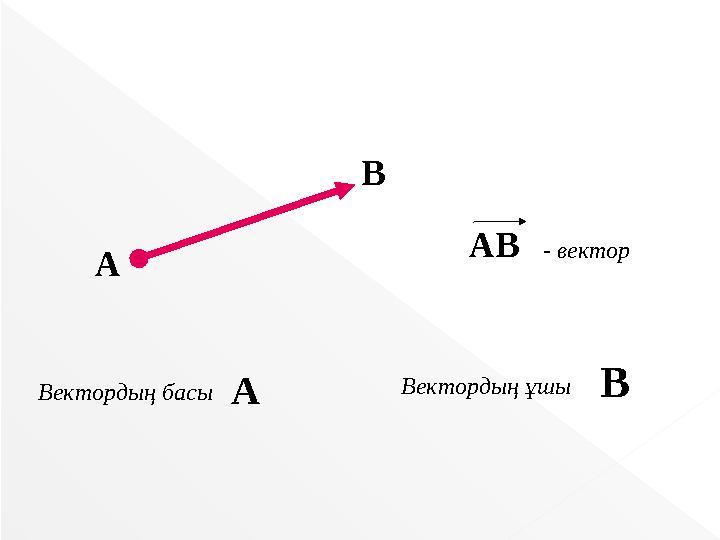
Белгіленуі: A B AB- вектор Вектордың ұшы Вектордың басы Анықтама. Кез келген бағытталған кесіндіні вектор деп атайды. "Вектор" (“vehere”) сөзін латын тілінен аударғанда, "әкелу", "жеткізу" деген мағынаны білдіреді. А В a

7 слайд

Белгіленуі: A B AB- вектор Вектордың ұшы Вектордың басы Анықтама. Кез келген бағытталған кесіндіні вектор деп атайды. "Вектор" (“vehere”) сөзін латын тілінен аударғанда, "әкелу", "жеткізу" деген мағынаны білдіреді. А В a

8 слайд
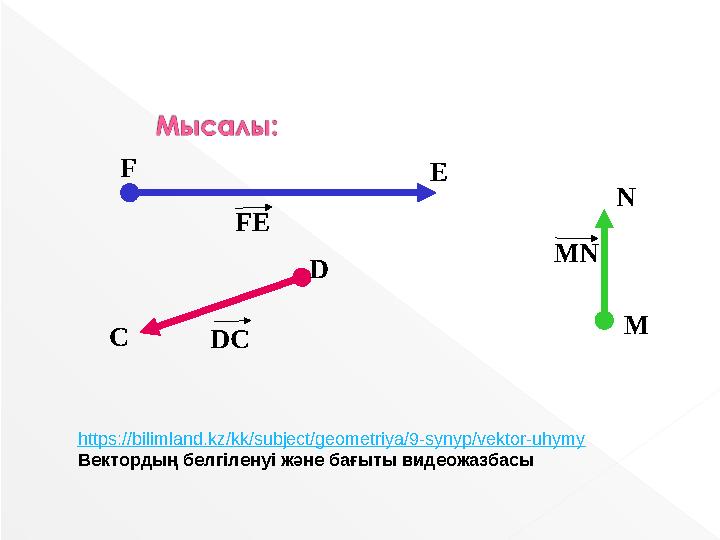
С D M N F E DC MN FE https://bilimland.kz/kk/subject/geometriya/9-synyp/vektor-uhymy Вектордың белгіленуі және бағыты видеожазбасы

8 слайд

С D M N F E DC MN FE https://bilimland.kz/kk/subject/geometriya/9-synyp/vektor-uhymy Вектордың белгіленуі және бағыты видеожазбасы

9 слайд
A B AB Вектордың ұшыВектордың басы - вектор ВА

9 слайд

A B AB Вектордың ұшыВектордың басы - вектор ВА

10 слайд
Анықтама. Басы мен ұшы беттесетін векторды нөлдік вектор деп атаймыз. Жазықтықтағы кез келген нүктені нөлдік вектор ретінде қарастыруымызға болады. Нөлдік векторды арқылы белгілейміз. ММ = 0 . 0 М

10 слайд

Анықтама. Басы мен ұшы беттесетін векторды нөлдік вектор деп атаймыз. Жазықтықтағы кез келген нүктені нөлдік вектор ретінде қарастыруымызға болады. Нөлдік векторды арқылы белгілейміз. ММ = 0 . 0 М

11 слайд
Анықтама. Векторды кескіндеп тұрған кесіндінің ұзындығы вектордың ұзындығы немесе абсолюттік шамасы (модулі) деп аталады. а 0АВ 00 AB А В a

11 слайд

Анықтама. Векторды кескіндеп тұрған кесіндінің ұзындығы вектордың ұзындығы немесе абсолюттік шамасы (модулі) деп аталады. а 0АВ 00 AB А В a

12 слайд
K M N a вектор MN немесе вектор а КК нольдік вектор Вектордың ұзындығы деп кесіндінің ұзындығын (немесе модулін) айтады |MN| = |a| MN векторының ұзындығы |KK| = 0

12 слайд

K M N a вектор MN немесе вектор а КК нольдік вектор Вектордың ұзындығы деп кесіндінің ұзындығын (немесе модулін) айтады |MN| = |a| MN векторының ұзындығы |KK| = 0

13 слайд
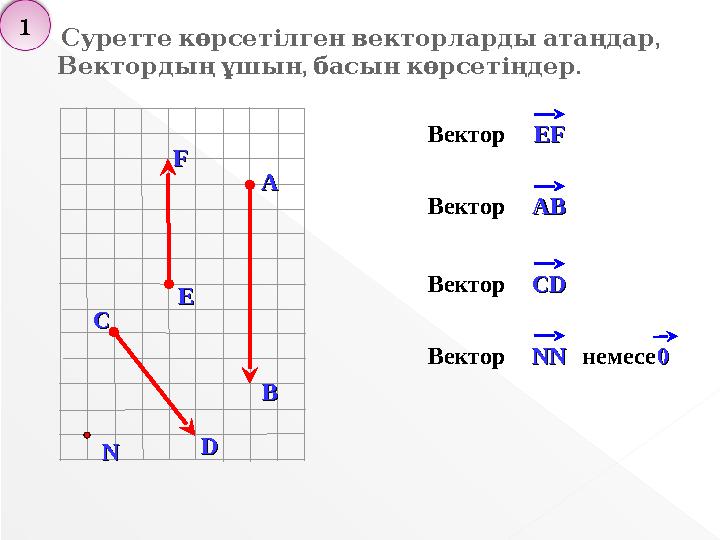
, Суреттекөрсетілгенвекторлардыатаңдар , . Вектордыңұшын басынкөрсетіңдер NN EE FF AA ВВ CC DD ЕЕFFВектор ABABВектор CDCDВектор NNNNВектор 00немесе 1

13 слайд

, Суреттекөрсетілгенвекторлардыатаңдар , . Вектордыңұшын басынкөрсетіңдер NN EE FF AA ВВ CC DD ЕЕFFВектор ABABВектор CDCDВектор NNNNВектор 00немесе 1

14 слайд
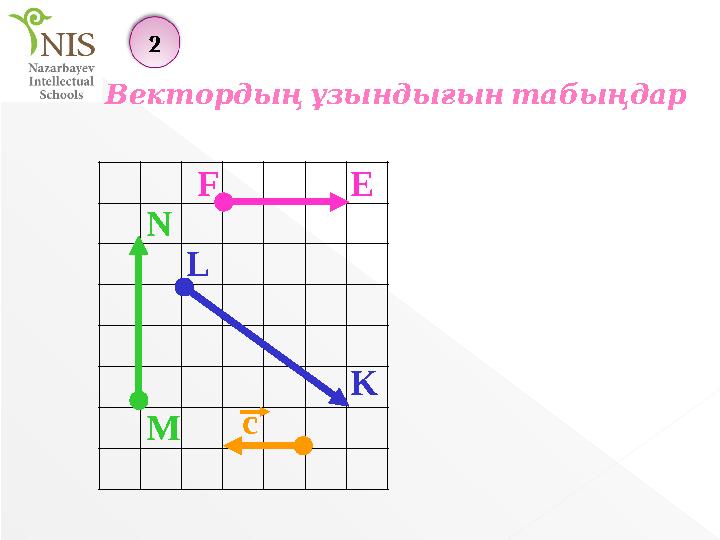
M N F E L K с Вектордыңұзындығынтабыңдар 2

14 слайд

M N F E L K с Вектордыңұзындығынтабыңдар 2

15 слайд
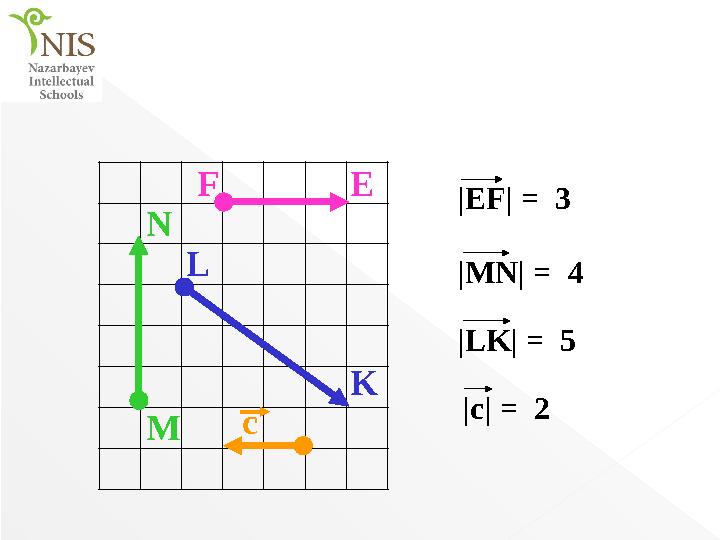
M N F E L K с |EF| = 3 |MN| = 4 |LK| = 5 |c| = 2

15 слайд

M N F E L K с |EF| = 3 |MN| = 4 |LK| = 5 |c| = 2

16 слайд
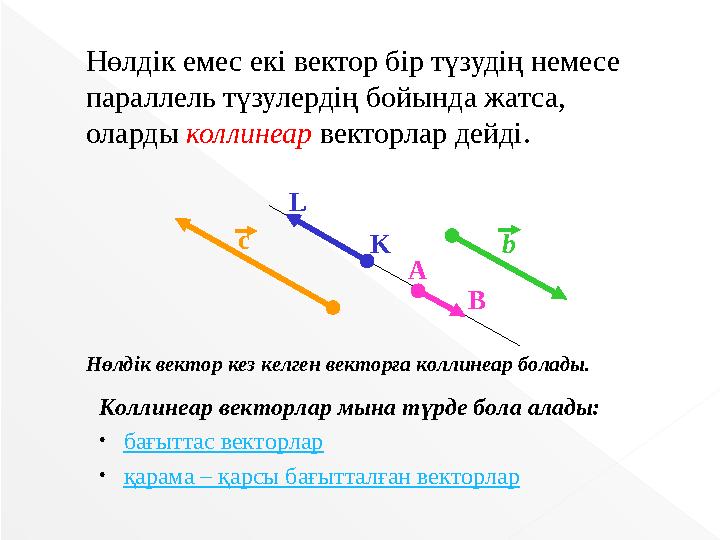
Нөлдік емес екі вектор бір түзудің немесе параллель түзулердің бойында жатса, оларды коллинеар векторлар дейді. с L K b A B Нөлдік вектор кез келген векторға коллинеар болады. Коллинеар векторлар мына түрде бола алады: • бағыттас векторлар • қарама – қарсы бағытталған векторлар

16 слайд

Нөлдік емес екі вектор бір түзудің немесе параллель түзулердің бойында жатса, оларды коллинеар векторлар дейді. с L K b A B Нөлдік вектор кез келген векторға коллинеар болады. Коллинеар векторлар мына түрде бола алады: • бағыттас векторлар • қарама – қарсы бағытталған векторлар

17 слайд
Нөлдік емес екі вектор бір түзуде немесе параллель түзулерде жатса, оларды коллинеар векторлар деп атайды. aa bb cc aabb ccaa ccbb Коллинеар, бағыттас векторларКоллинеар, бағыттас векторлар ooaa oocc oobb Нөлдік вектор Нөлдік вектор ,кез келген вектормен бағыттас және коллинеар болады.

17 слайд

Нөлдік емес екі вектор бір түзуде немесе параллель түзулерде жатса, оларды коллинеар векторлар деп атайды. aa bb cc aabb ccaa ccbb Коллинеар, бағыттас векторларКоллинеар, бағыттас векторлар ooaa oocc oobb Нөлдік вектор Нөлдік вектор ,кез келген вектормен бағыттас және коллинеар болады.

18 слайд
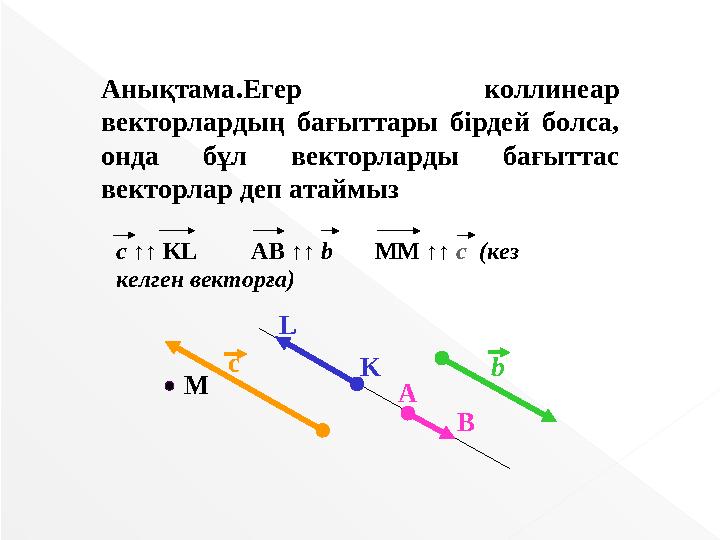
с L K b A B Анықтама.Егер коллинеар векторлардың бағыттары бірдей болса, онда бұл векторларды бағыттас векторлар деп атаймыз М c ↑↑ KL AB ↑↑ b MM ↑↑ c (кез келген векторға)

18 слайд

с L K b A B Анықтама.Егер коллинеар векторлардың бағыттары бірдей болса, онда бұл векторларды бағыттас векторлар деп атаймыз М c ↑↑ KL AB ↑↑ b MM ↑↑ c (кез келген векторға)

19 слайд
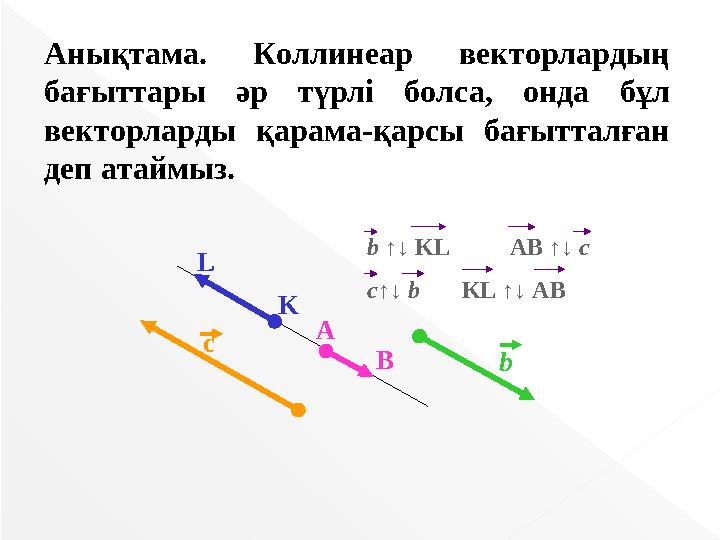
с b L K A B Анықтама. Коллинеар векторлардың бағыттары әр түрлі болса, онда бұл векторларды қарама-қарсы бағытталған деп атаймыз. b ↑↓ KL AB ↑↓ c c↑↓ b KL ↑↓ AB

19 слайд

с b L K A B Анықтама. Коллинеар векторлардың бағыттары әр түрлі болса, онда бұл векторларды қарама-қарсы бағытталған деп атаймыз. b ↑↓ KL AB ↑↓ c c↑↓ b KL ↑↓ AB

20 слайд
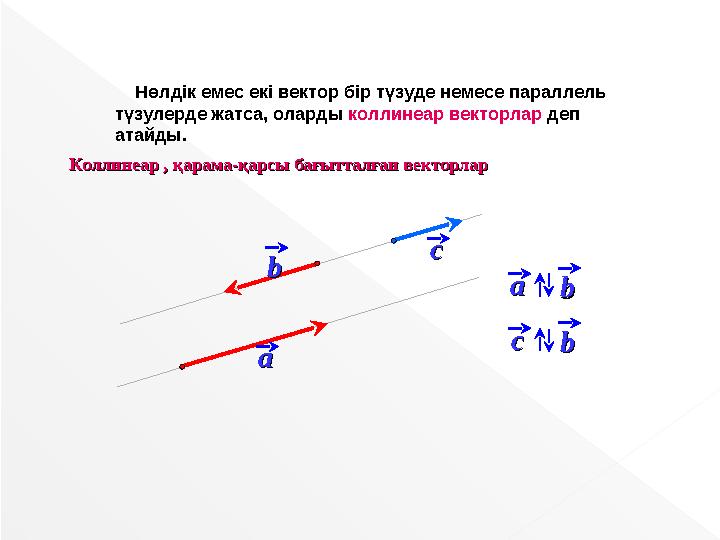
Нөлдік емес екі вектор бір түзуде немесе параллель түзулерде жатса, оларды коллинеар векторлар деп атайды. aa bb cc bbaa Коллинеар , қарама-қарсы бағытталған векторларКоллинеар , қарама-қарсы бағытталған векторлар bbcc

20 слайд

Нөлдік емес екі вектор бір түзуде немесе параллель түзулерде жатса, оларды коллинеар векторлар деп атайды. aa bb cc bbaa Коллинеар , қарама-қарсы бағытталған векторларКоллинеар , қарама-қарсы бағытталған векторлар bbcc

21 слайд
Анықтама. Ұзындықтары тең, бағыттары қарама – қарсы векторларлар - қарама – қарсы векторлар деп аталады. Нөлдік векторға қарама – қарсы вектор нөлдік вектор болады. a b bababa  ,

21 слайд

Анықтама. Ұзындықтары тең, бағыттары қарама – қарсы векторларлар - қарама – қарсы векторлар деп аталады. Нөлдік векторға қарама – қарсы вектор нөлдік вектор болады. a b bababa  ,

22 слайд

23 слайд
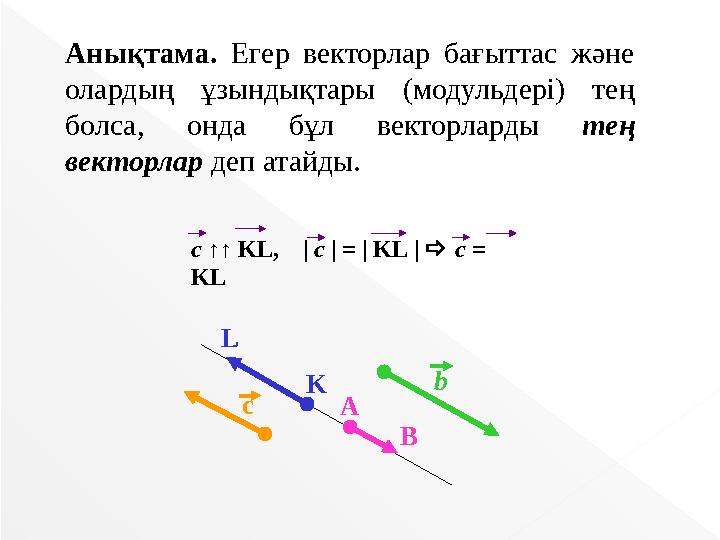
Анықтама. Егер векторлар бағыттас және олардың ұзындықтары (модульдері) тең болса, онда бұл векторларды тең векторлар деп атайды. c ↑↑ KL, | c | = | KL |  c = KL с L K b A B

23 слайд

Анықтама. Егер векторлар бағыттас және олардың ұзындықтары (модульдері) тең болса, онда бұл векторларды тең векторлар деп атайды. c ↑↑ KL, | c | = | KL |  c = KL с L K b A B

24 слайд
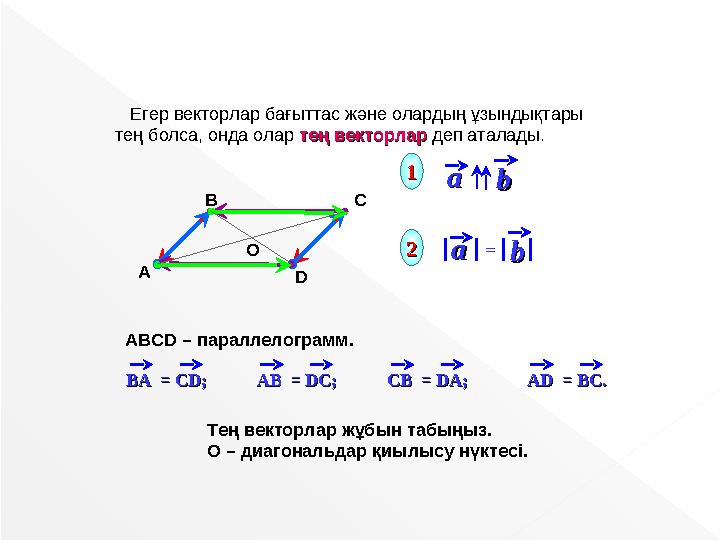
АВСD – параллелограмм. А В С D bbaa Егер векторлар бағыттас және олардың ұзындықтары тең болса, онда олар тең векторлар тең векторлар деп аталады. a a bb == 11 22 ВВA = CDA = CD;; AAВВ = DC = DC;; CCВВ = DA = DA;; AD = BCAD = BC.. О Тең векторлар жұбын табыңыз. О – диагональдар қиылысу нүктесі.

24 слайд

АВСD – параллелограмм. А В С D bbaa Егер векторлар бағыттас және олардың ұзындықтары тең болса, онда олар тең векторлар тең векторлар деп аталады. a a bb == 11 22 ВВA = CDA = CD;; AAВВ = DC = DC;; CCВВ = DA = DA;; AD = BCAD = BC.. О Тең векторлар жұбын табыңыз. О – диагональдар қиылысу нүктесі.

25 слайд
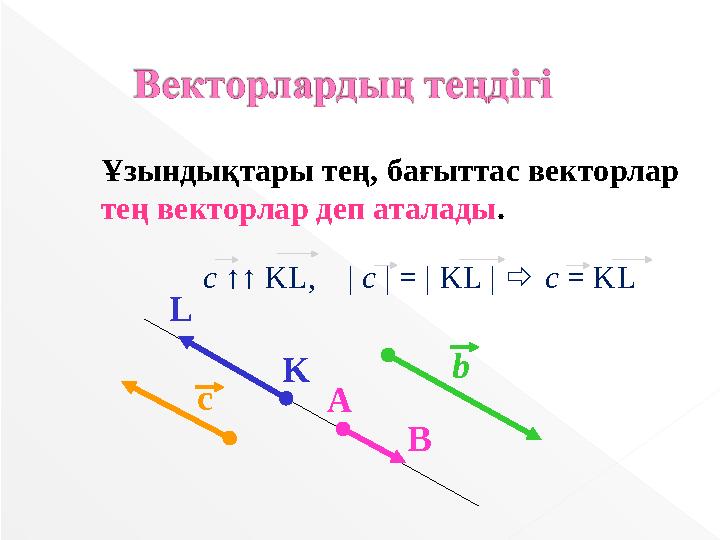
с L K b A B Ұзындықтары тең, бағыттас векторлар тең векторлар деп аталады. c ↑↑ KL, | c | = | KL |  c = KL

25 слайд

с L K b A B Ұзындықтары тең, бағыттас векторлар тең векторлар деп аталады. c ↑↑ KL, | c | = | KL |  c = KL

26 слайд
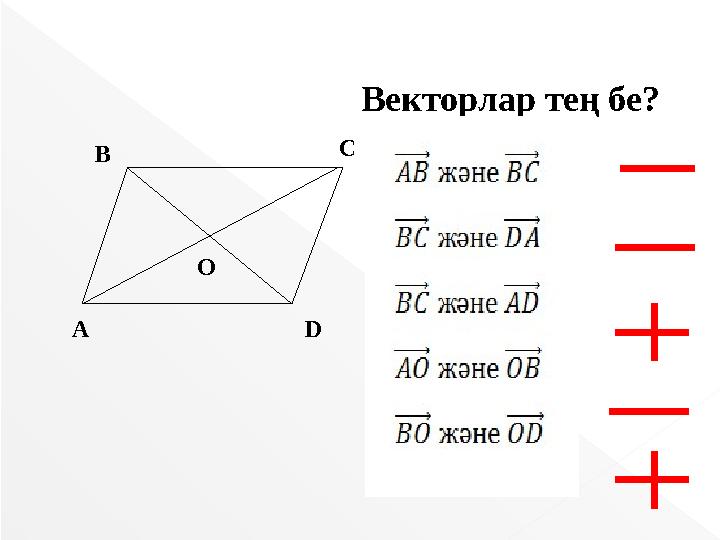
А В С D O Векторлар тең бе?

26 слайд

А В С D O Векторлар тең бе?

27 слайд
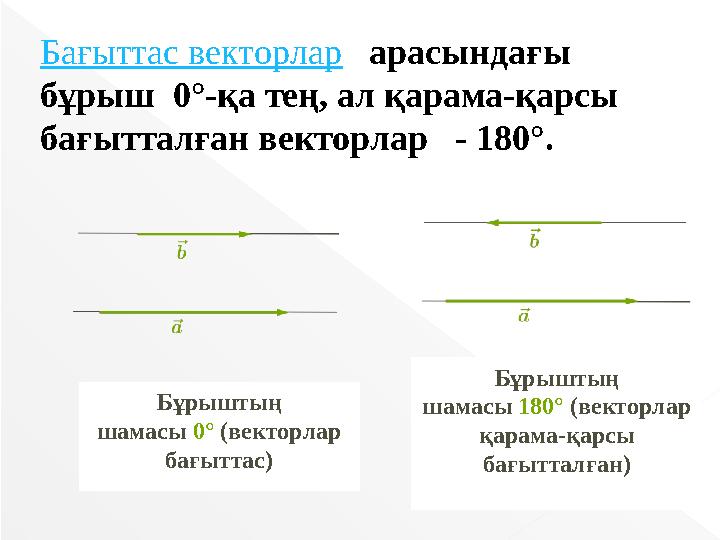
Бағыттас векторлар арасындағы бұрыш 0°-қа тең, ал қарама-қарсы бағытталған векторлар - 180°. Бұрыштың шамасы 0° (векторлар бағыттас) Бұрыштың шамасы 180° (векторлар қарама-қарсы бағытталған)

27 слайд

Бағыттас векторлар арасындағы бұрыш 0°-қа тең, ал қарама-қарсы бағытталған векторлар - 180°. Бұрыштың шамасы 0° (векторлар бағыттас) Бұрыштың шамасы 180° (векторлар қарама-қарсы бағытталған)

28 слайд
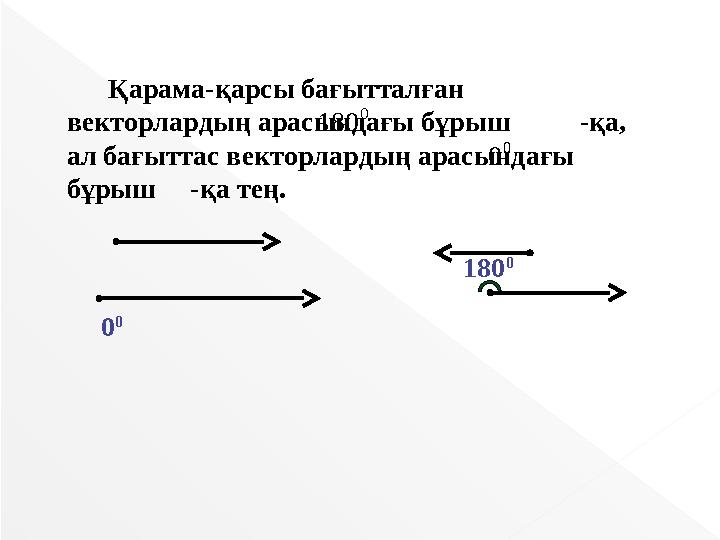
Қарама-қарсы бағытталған векторлардың арасындағы бұрыш -қа, ал бағыттас векторлардың арасындағы бұрыш -қа тең. 0 180 0 0 180 0 0 0

28 слайд

Қарама-қарсы бағытталған векторлардың арасындағы бұрыш -қа, ал бағыттас векторлардың арасындағы бұрыш -қа тең. 0 180 0 0 180 0 0 0

29 слайд
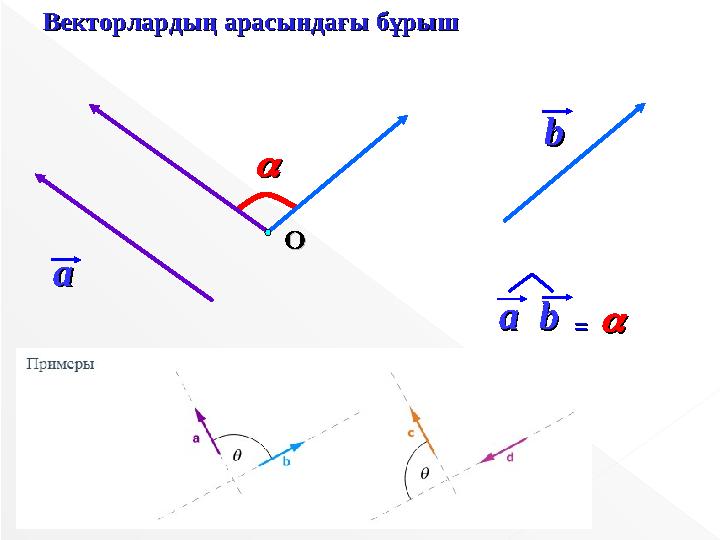
aa bb aabb ==  ОО Векторлардың арасындағы бұрышВекторлардың арасындағы бұрыш

29 слайд

aa bb aabb ==  ОО Векторлардың арасындағы бұрышВекторлардың арасындағы бұрыш

30 слайд

31 слайд
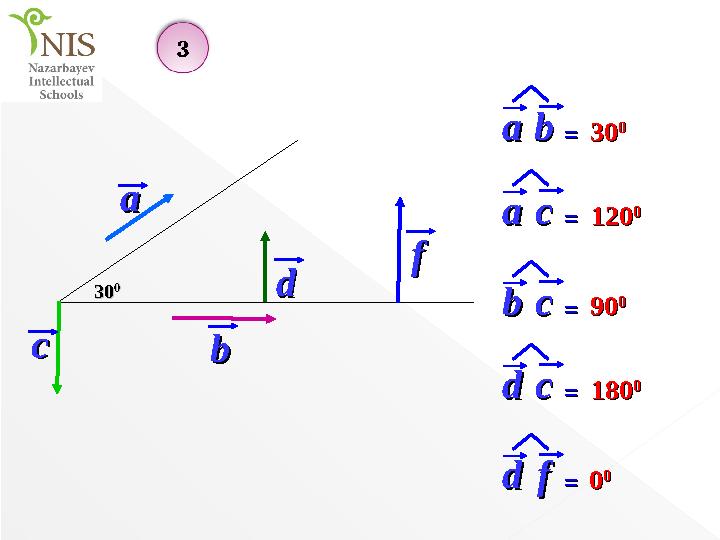
aa dd bb 3030 00 aabb == cc ff 3030 00 aacc == bbcc == ddff == ddcc == 120120 00 9090 00 180180 00 00 00 3

31 слайд

aa dd bb 3030 00 aabb == cc ff 3030 00 aacc == bbcc == ddff == ddcc == 120120 00 9090 00 180180 00 00 00 3

32 слайд
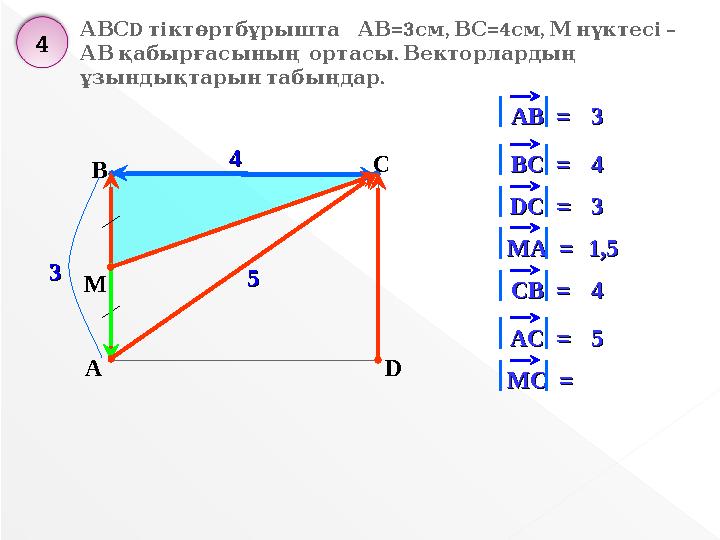
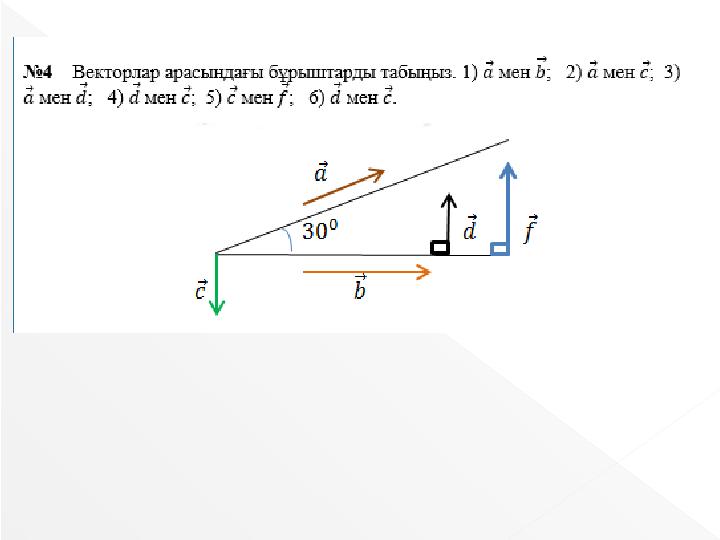
С А В D 44 33 АВАВ = =33 ВВC =C =44 DDСС = =33 MMАА = =1,51,5 СВСВ = =44 АСАС = = 55 55 ММC =C = M АВСD тіктөртбұрышта =3 , =4 , – АВ см ВС см Мнүктесі . АВқабырғасының ортасы Векторлардың . ұзындықтарынтабыңдар 4

32 слайд

С А В D 44 33 АВАВ = =33 ВВC =C =44 DDСС = =33 MMАА = =1,51,5 СВСВ = =44 АСАС = = 55 55 ММC =C = M АВСD тіктөртбұрышта =3 , =4 , – АВ см ВС см Мнүктесі . АВқабырғасының ортасы Векторлардың . ұзындықтарынтабыңдар 4

33 слайд
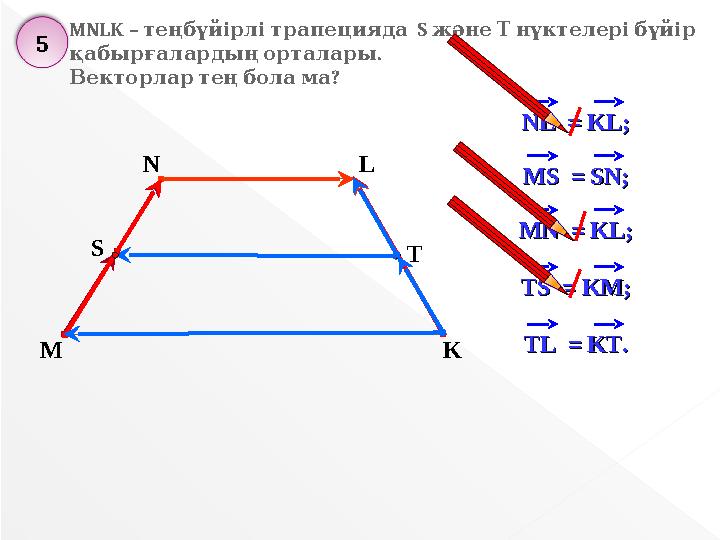
MNLK – теңбүйірлітрапецияда S жәнеТнүктелерібүйір . қабырғалардыңорталары ? Векторлартеңболама M N L K NL = KLNL = KL;; MS = SNMS = SN;; MN = KLMN = KL;; TS = KM;TS = KM; S T TL = KT.TL = KT. 5

33 слайд

MNLK – теңбүйірлітрапецияда S жәнеТнүктелерібүйір . қабырғалардыңорталары ? Векторлартеңболама M N L K NL = KLNL = KL;; MS = SNMS = SN;; MN = KLMN = KL;; TS = KM;TS = KM; S T TL = KT.TL = KT. 5

34 слайд
№2. Сурет бойынша векторларды табыңыз: №2. Сурет бойынша векторларды табыңыз:•Коллинеар векторларды; •Бағыттас векторларды; •Қарама-қарсы векторларды. •Коллинеар векторларды; •Бағыттас векторларды; •Қарама-қарсы векторларды.

34 слайд

№2. Сурет бойынша векторларды табыңыз: №2. Сурет бойынша векторларды табыңыз:•Коллинеар векторларды; •Бағыттас векторларды; •Қарама-қарсы векторларды. •Коллинеар векторларды; •Бағыттас векторларды; •Қарама-қарсы векторларды.

35 слайд

36 слайд