Векторлардың скаляр көбейтіндісі

1 слайд
Векторлардың скаляр көбейтіндісіСабақтың тақырыбы: Шығыс Қазақстан облысы білім басқармасы Үржар ауданы бойынша білім бөлімінің «Ахмет Байтұрсынұлы атындағы орта мектебі» КММ математика пәнінің мұғалімі Ибраева Айгерим Саматовна Геометрия 10 сынып

2 слайд
Сабақ мақсаты: Оқушыларға векторлардың скаляр көбейтіндісі туралы түсінік беру, оған байланысты есептерді шығаруға үйрету. Оқушылардың ойлау қабілетін, тест тапсырмаларын орындау ептілігін арттыру, дамыту. Оқушыларды өз білімдерін жүйелеуге, ұқыптылыққа және нақтылыққа тәрбиелеу.

3 слайд
Қайталау сұрақтары

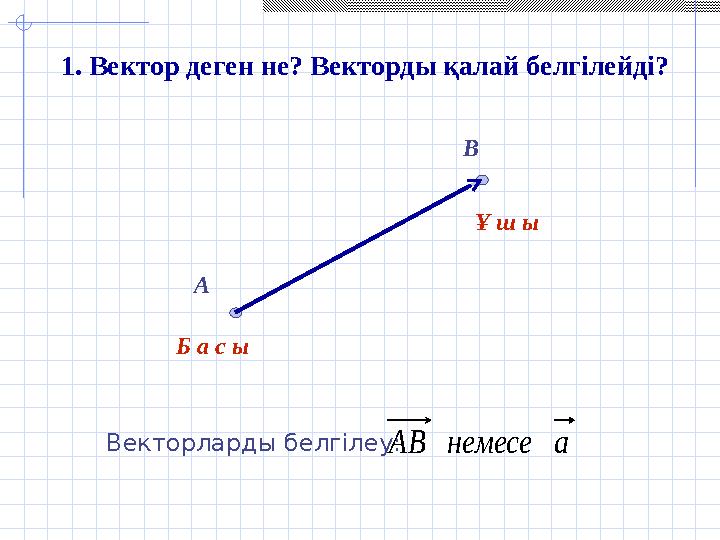
4 слайд
А В Б а с ы Ұ ш ы Векторларды белгілеу:а немесе АВ1. Вектор деген не? Векторды қалай белгілейді?

5 слайд
2. Нөлдік вектор деген не?

6 слайд
Егер в ектордың бас нүктесі оның ұшымен дәл келіп беттесіп жатса, онда ол векторды нөлдік вектор деп атайды және деп белгілейді. Нөлдік вектордың абсолют шамасы нөлге тең.0  0 0  2. Нөлдік вектор деген не?

7 слайд
3. Вектордың абсолют шамасы деген не?

8 слайд
Вектордың абсолют шамасы немесе модулі деп векторды кескіндейтін кесіндінің ұзындығын атайды және деп белгілейді. АВ а ,  ) ; ; ( 2 2 2 z у х В ) ; ; ( 1 1 1 z у х А ) ; ; ( 3 2 1 а а а а  2 3 2 2 2 1 а а а а     2 1 2 2 1 2 2 1 2 ) ( ) ( ) ( z z у у х х АВ      3. Вектордың абсолют шамасы деген не?

9 слайд
b а    b а    а  b Векторлардың теңдігі 4. Қандай векторлар тең деп аталады?

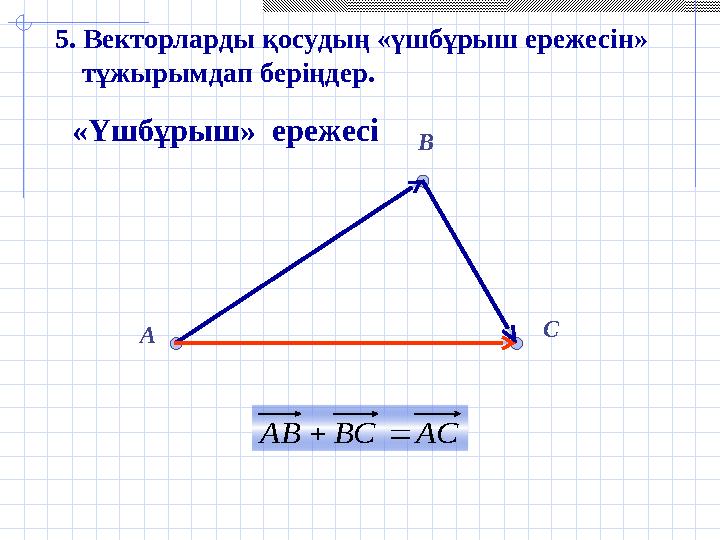
10 слайд
A B CАС ВС АВ  «Үшбұрыш» ережесі5. Векторларды қосудың «үшбұрыш ережесін» тұжырымдап беріңдер.АС ВС АВ  

11 слайд
6. Векторлар үшін “параллелограмм” ережесін тұжырымдап беріңдер.

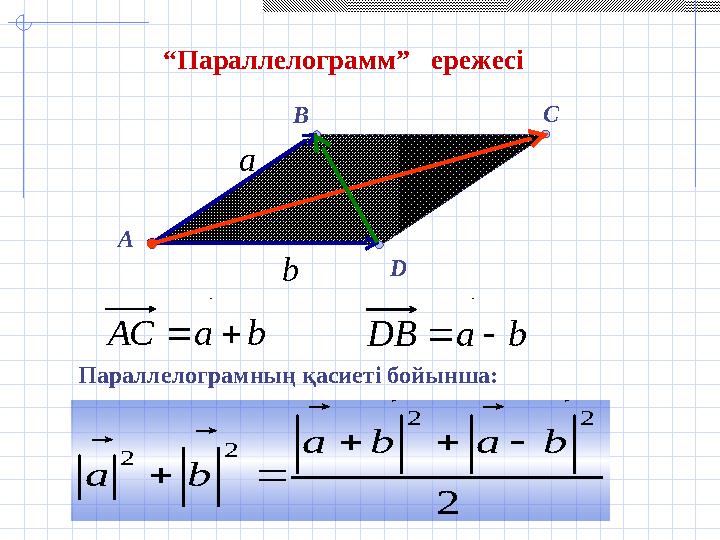
12 слайд
C A B D“ Параллелограмм” ережесіа  b  b а АС     b а DВ     Параллелограмның қасиеті бойынша: 2 2 2 2 2 b a b a b а           

13 слайд
7. Қандай векторлар коллинеар векторлар деп аталады? Қоллинеар векторлардың қасиеті.

14 слайд

15 слайд
Бір түзу бойында немесе параллель түзулер бойында жатқан нөлдік емес екі вектор коллинеар векторлар деп аталады. Коллинер векторлардың сәйкес координаталары пропорционал болады. Белгілеуі: а  b  ) ; ; ( 3 2 1 a a a a  ) ; ; ( 3 2 1 b b b b  3 3 2 2 1 1 b a b a b a  

16 слайд
8. Қандай векторлар орттар деп аталады?

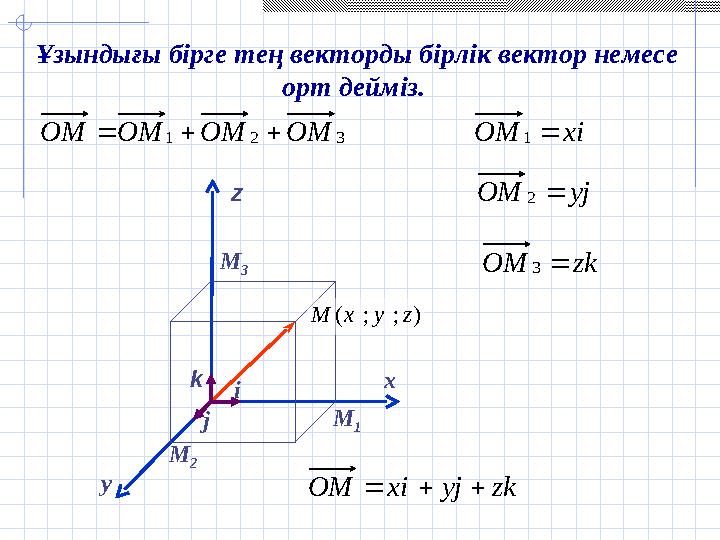
17 слайд
) ; ; ( z y x Mi jk x y z M 1 M 2 M 3Ұзындығы бірге тең векторды бірлік вектор немесе орт дейміз. 3 2 1 ОМ ОМ ОМ ОМ    i x ОМ   1 j y ОМ   2 k z ОМ   3 k z j y i x ОМ      

18 слайд
Векторлардың скаляр Векторлардың скаляр көбейтіндісікөбейтіндісіЖаңа сабақЖаңа сабақ

19 слайд
 cos     b а b a    21-теорема. Векторлардың скаляр көбейтіндісі олардың модульдерін сол векторлар арасындағы бұрыштың косинусына көбейткенде шығатын санға тең болады, яғни Бұдан, . 0 b a b a         cos     b а b a     . 0 b a b a        

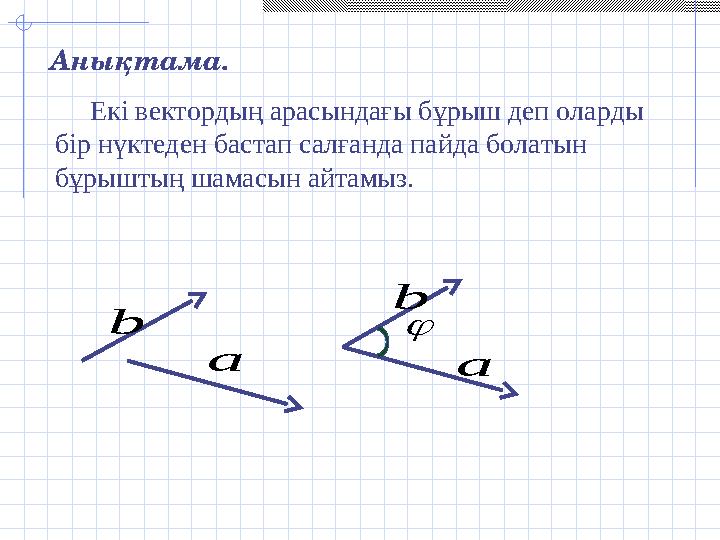
20 слайд
 b Аны қтама. Екі вектордың арасындағы бұрыш деп оларды бір нүктеден бастап салғанда пайда болатын бұрыштың шамасын айтамыз. b  а  а 

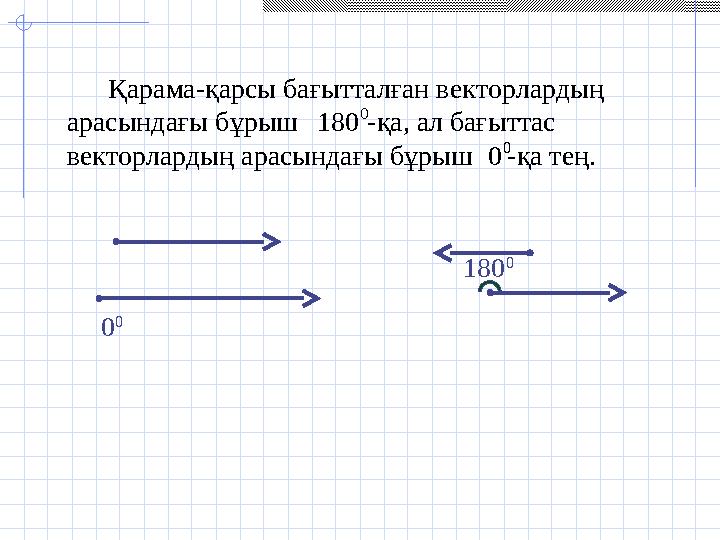
21 слайд
Қарама-қарсы бағытталған векторлардың арасындағы бұрыш -қа, ал бағыттас векторлардың арасындағы бұрыш -қа тең.0 180 0 0 180 0 0 0

22 слайд
Скаляр көбейтіндінің жазықтықта келтірілген төрт қасиеті: 1) 2) 3) 4)) ; ; ( 3 2 1 b b b b  ; 0 2    а a a    мен векторларының скаляр көбейтіндісі деп санын айтамыз. 3 3 2 2 1 1 b a b a b a b a       3 3 2 2 1 1 b a b a b a b a       3 3 2 2 1 1 b a b a b a  Аны қтама. ) ; ; ( 3 2 1 a a a a  ) ; ; ( 3 2 1 b b b b  ; a b b a        ; ) ( c b с a с b a              ) ( ) ( b a b a            кеңістікте де сақталады.

23 слайд
Есеп . және векторларының арасындағы бұрыштың косинусын табыңдар. Ш ешуі: ) 2 ; 2 ; 1(  а  ) 0; 3; 4 (  b  . cos b a b а          Бұдан 3 2 5 3 10 0 3 ) 4 ( 2 ) 2 ( 1 0 2 3 ) 2 ( ) 4 ( 1 cos 2 2 2 2 2                        b a b a      Жауабы : 3 2 cos   . cos b a b а          3 2 5 3 10 0 3 ) 4 ( 2 ) 2 ( 1 0 2 3 ) 2 ( ) 4 ( 1 cos 2 2 2 2 2                        b a b a      3 2 cos   

24 слайд
№ 211 есеп. Мына векторлардың скаляр көбейтіндісін табыңдар:) 4 ; 2 ; 1( à  ) 1; 2 ; 8 (  b  және 1)

25 слайд
№ 211 есеп. Мына векторлардың скаляр көбейтіндісін табыңдар:) 1; 3 ; 2 (   p  ) 1; 3; 2 ( q  және 2)

26 слайд
№ 212 есеп. n – нің қандай мәндерінде:) 3; 1 ; 2 (  а  1 ) және векторлары перпендикуляр болады? ) ; 3; 1( n b 

27 слайд
№ 212 есеп. n – нің қандай мәндерінде:) 1; 2 ; (  n à  ) 1; ; ( n n b   және2) векторлары перпендикуляр болады?

28 слайд
№ 213 есеп. ) 1; 2 ; 2 (  т  ) 1; 0; 1 (  n  және векторларының арасындағы бұрышты табыңдар.

29 слайд
№ 214 есеп. Төрт нүкте берілген: A(0;1;-1), B(1;-1;2), C(3;1;0), D(2;-3;1) . және векторларының арасындағы бұрыштың косинусын табыңдар.AB CD

30 слайд

31 слайд
Бекіту сұрақтары

32 слайд
1) Қандай векторларды бағыттас векторлар деп атаймыз? 2) Қандай векторларды қарама – қарсы бағытталған векторлар деп атаймыз? 3)Қай кезде екі вектор арасындағы бұрыш 180 °-қа тең болады? 4) Қай кезде екі вектор арасындағы бұрыш 0°-қа тең болады? 5) Қай кезде екі вектор арасындағы бұрыш тік болады? 6) Қай кезде екі вектор арасындағы бұрыш сүйір болады? 7) Қай кезде екі вектор арасындағы бұрыш доғал болады? 8)Екі вектордың скалярлық көбейтіндісін қалай табамыз?

33 слайд
Үйге тапсырма: № 215, №216 есептер.