Виет теоремасы

1 слайд
Виет теоремасы Алгебра 8 сынып

1 слайд

2 слайд
Сабақ мақсаты: 1. Виет теоремасын тұжырымдау және дәлелдеу. Квадрат теңдеулерді түбірлердің қасиеттерін қолдану арқылы шешуді үйрету; 2. Оқушыларға Виет теоремасын қолдану тәсілдерімен таныстыру және квадрат теңдеулерді шешуді үйрету; 3. Виет теоремасын қолдана отырып есептер шығаруға оқушыларды баулу және дағдыландыру.

2 слайд

3 слайд
Қайталау сұрақтары: 1. түріндегі теңдеу қалай аталады? 2. формуласымен есептелетін сан қалай аталады? 3. Егер D>0 болса, онда квадраттық теңдеудің неше түбірі болады? 4. Егер D = 0 болса, онда квадраттық теңдеудің неше түбірі болады? 5. Егер D<0 болса, онда квадраттық теңдеудің неше түбірі болады? 6. Қандай жағдайда квадраттық теңдеу келтірілген квадраттық теңдеу деп атайды? 7. теңдеуінің коэффициенттерін атап шығыңдар. 8. Егер квадраттық теңдеуінде коэффициенттердің бірі – b не с немесе b мен с-ның екеуі де 0-ге тең болса, мұндай теңдеулерді қалай атайды?0 2    c bx ах ac b 4 2  0 3 5 2 2    х х

3 слайд

4 слайд
 Түбірлері бар бірнеше келтірілген квадраттық теңдеудің түбірлерін, түбірлерінің қосындысы мен көбейтіндісінің мәндерін табыңдар және жауаптарын кестеге толтырыңдар. Теңдеулер Түбірлер х 1 және х 2 х 1 + х 2 х 1 · х 2 х 2 – 2х – 3 = 0 Х 2 + 5х – 6 = 0 х 2 – х – 12 = 0 х 2 + 7х + 12 = 0 х 2 – 8х + 15 = 0

4 слайд

5 слайд
Бұл мысалдардан, келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең екенін байқадық. Енді бұл қасиетті теорема ретінде тұжырымдап шығайық. Теорема : Келтірілген квадраттық теңдеу түбірлерінің қосындысы қарсы таңбасымен алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болады: q x x p х х      2 1 2 1 ;

5 слайд

6 слайд
(келтірілген квадрат теңдеу) – екінші коэффициент – бос мүше Теңдеудің дискриминанті: Егер D > 0, о нда теңдеудің екі түбірі бар: және Түбірлердің қосындысы: Түбірлердің көбейтіндісі: . Сонымен, 2 1 D р х    2 2 D р х    p p D р D р х х           2 2 2 2 1             4 ) ( ) ( 2 2 ) ( ) ( 2 2 2 1 D p D р D р х х q q p p D p       4 ) 4 ( 4 2 2 2 0 2    q px x p q q p D 4 2   p х х    2 1 q х х   2 1

6 слайд

7 слайд
Бұл теореманы бірінші дәлелдеген француз математигі Француа Виет (1540-1603) болғандықтан, соның атымен аталады. Кейбір есептерді шешкенде Виет теоремасына кері теореманы қолданады. Теорема (кері теорема). Егер сандары үшін шарттары орындалса, онда сандары теңдеуінің түбірлері болады. 2 1 , , , x x q p q x x p х х      2 1 2 1 , 2 1 x мен x 0 2    q px х

7 слайд

8 слайд
Виет теоремасы ж әне оған кері теорема теңдеуді шешпей-ақ , түбірлерінің қосындысы мен көбейтіндісін табуға және түбірлері белгілі болғанда, теңдеуді құруға мүмкіндік береді. Мысал қарастырайық: Түбірлері және болған квадраттық теңдеуді құрайық: 3 2 1   õ 3 2 2   õ 0 ) 3 2 )( 3 2 ( ) 3 2 3 2 ( 2         õ õ 0 1 4 2    õ õ

8 слайд

9 слайд
Теңдеулер Түбірлерінің қосындысы Түбірлерінің көбейтіндісі0 35 2 2    õ õ 0 3 4 2    õ õ 0 7 8 2    õ õ 0 9 8 2    õ õ 0 11 10 2    õ õ 0 1 4 2    õ õ№ 257

9 слайд

10 слайд
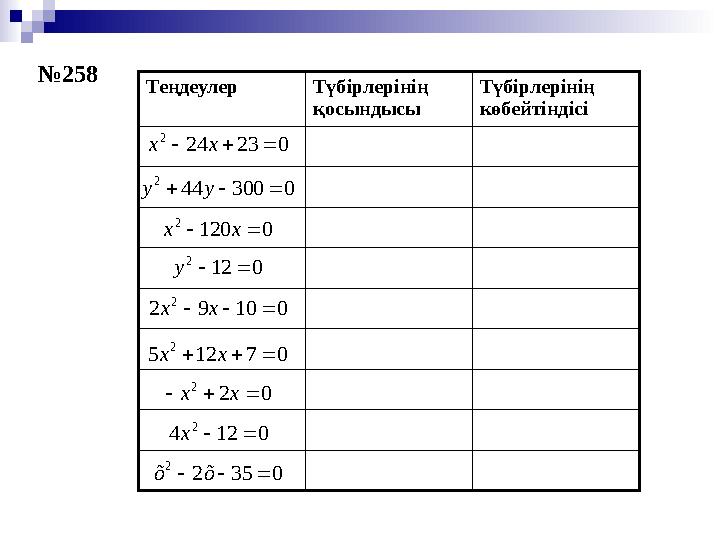
Теңдеулер Түбірлерінің қосындысы Түбірлерінің көбейтіндісі0 23 24 2    х х№ 258 0 300 44 2    у у 0 120 2   х х 0 12 2   у 0 10 9 2 2    х х 0 7 12 5 2    х х 0 2 2    х х 0 12 4 2   х 0 35 2 2    õ õ

10 слайд

11 слайд
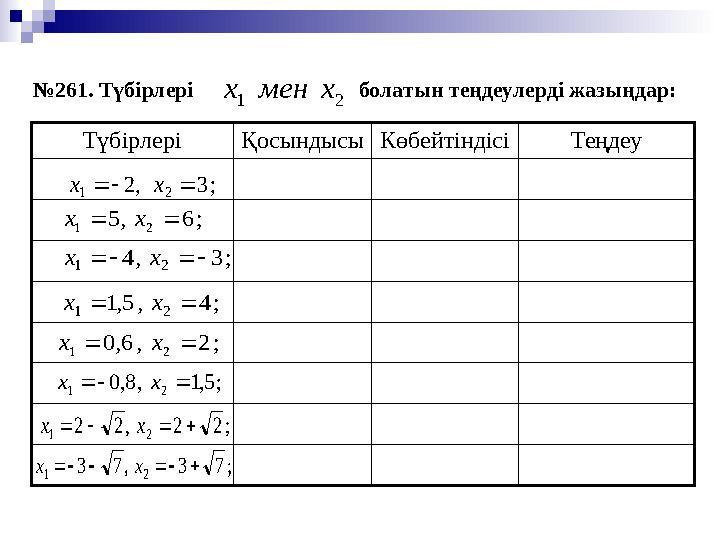
№ 261. Т үбірлері болатын теңдеулерді жазыңдар: 2 1 х мен х ; 3 , 2 2 1    х х Түбірлері Қосындысы Көбейтіндісі Теңдеу ; 6 , 5 2 1   х х ; 3 , 4 2 1     х х ; 4 , 5, 1 2 1   х х ; 2 , 6, 0 2 1   х х ; 5,1 , 8, 0 2 1    х х ; 2 2 , 2 2 2 1     х х ; 7 3 , 7 3 2 1       х х

11 слайд

12 слайд
1. х 2 - 12х + с = 0 теңдеуінің бір түбірі х 1 =5. х 1 + х 2 =12 және х 1 · х 2 =с. с-ны табыңдар. 2. х 2 +рх + 15 = 0 теңдеуінің бір түбірі х 1 =3. х 1 + х 2 = -р және х 1 · х 2 =15. р-ны табыңдар. 3. Теңдеулерді шешіп Виет теоремасы және кері теорема арқылы тексеріңдер: а) х 2 - 9х + 8 = 0, б) х 2 + 12х + 20 = 0, в) х 2 - 4х - 21 = 0.

12 слайд

13 слайд
Тест сұрақтары: 1. Берілген теңдеудің түбірлерінің қосындысы мен көбейтіндісін табыңдар: А) 8; 15 В) -8; 15 С) 8; -15 D ) -8; -15 Е) 5; -18 2. Түбірлері болатын теңдеуді жазыңдар: А) В) С) D ) Е) 3. теңдеуінің бір түбірі 7-ге тең. Екінші түбірін және р -ны табыңдар. А) 2; 5 В) -2; 5 С) -5; -2 D ) 2; -5 Е) 5; -1. 4. Теңдеудің түбірлерін табыңдар: А) 11; 10 В) -1; 10 С) 1; 10 D ) 1; -10 Е) -1; -10 5. Келтірілген квадраттық теңдеуді көрсет: А) В) С) D ) Е)7 ,1 2 1     х х 0 15 8 2    х х 0 7 8 2    х х 0 15 8 2    х х 0 7 8 2    х х 0 35 2    рх х 0 7 8 2    х х 0 7 8 2    х х 0 10 11 2    х х 0 3 8 5 2    х х 0 1 5 2 2    х х 0 5 3 2    х х 0 15 8 2    х х 0 15 9 2    х х

13 слайд

14 слайд

14 слайд

15 слайд
Те ңдеулердің түбірлерінің қосындысы мен көбейтіндісін табыңдар:

15 слайд

16 слайд
Үйге тапсырма: § 3. № 259, №260 79 бет

16 слайд