Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз

Бонусты жинап картаңызға (kaspi Gold, Halyk bank) шығарып аласыз
1 жыл бойы тегін жүктеу мүмкіндігіне ие болыңыз!

жеңілдік
10 сынып геометрия ЖМБ бжб, тжб. 1 тоқсан

Жаратылыстану-математикалық бағыты
1 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ ТАПСЫРМАЛАРЫ
«Стереометрия аксиомалары. Кеңістіктегі параллельдік»
бөлімі бойынша жиынтық бағалау
|
Тақырып |
Стереометрия аксиомалары және олардың салдарлары. Кеңістіктегі түзулердің өзара орналасуы |
||
|
|
Түзу мен жазықтықтың өзара орналасуы. Жазықтықтардың параллельдігі |
|
|
|
|
|
|
|
|
Оқыту мақсаттары |
10.2.2 Кеңістіктегі параллель және айқас түзулер анықтамаларын білу, оларды анықтау және кескіндеу |
||
|
|
10.2.3 Кеңістіктегі параллель түзулердің қасиеттерін білу және оларды есептер шығаруда қолдану |
|
|
|
|
10.2.4 Түзу мен жазықтықтың параллельдік белгісін және қасиеттерін білу, оларды есептер шығаруда қолдану |
||
|
|
10.1.2.5 Жазықтықтардың параллельдік белгісін және қасиеттерін білу, оларды есептер шығаруда қолдану |
|
|
|
Бағалау критерийлері Білім алушы: -Кеңістіктегі түзулердің өзара орналасуын анықтайды |
|
|
|
|
|
|
||
-Параллель түзулердің қасиеттерін қолданады
-Түзу мен жазықтықтың параллельдігін қолданады
-Жазықтықтардың параллельдік белгілерін және
қасиеттерін қолданады
Ойлау дағдыларының Білу және түсіну
деңгейі Қолдану
Орындау уақыты 20 минут
Тапсырмалар
І нұсқа
-
Бір түзудің бойында жатпайтын төрт нүкте арқылы неше жазықтық жүргізуге болады. Жауабын негіздеңіз[3]
-
M нүктесі ABCD параллелограмы жазықтығынан тыс орналасқан(сурет).Бүйір жақтарының орта сызығынан құралған параллелограм периметрі 24см, ал BC=2AВболса, онда:
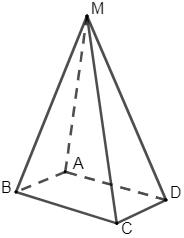
-
Параллелограмм периметрін [2]
-
Параллелограмм қабырғаларын анықтаңыз. [2]
-
АВС үшбұрышының ВС қабырғасына параллель жазықтық Оның АВ қабырғасын D нүктесінде, АС қабырғасынЕ нүктесінде қиып өтеді.Егер АВ=12, BC=10 және AD:DB=3:2 болса, DE кесіндісінің ұзындығын табыңыз. [3]
-
Өзара параллель екі жазықтық DEK бұрышының ED сәулесін A және B нүктелерінде, EKсәулесінCжәнеNнүктелерінде қиып өтеді жәнеEA=6см,EB=10см,EC=9смболса, CN-ді табыңыз.[4]
ІI нұсқа
-
Қиылыспайтын екі түзу арқылы неше жазықтық жүргізуге болады. Жауабын негіздеңіз [3]
-
ABCDA1B1C1D1кубы бейнеленген.
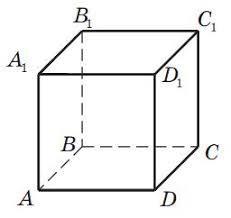
а)AжәнеA1 төбелері арқылы өтетін түзуге параллель қырларын көрсетіңіз[2]
б) CD-ға айқасқырларын анықтаңыз. [2]
-
Тік бұрышты параллелепипедтің табаны-шаршы. Оның диагоналі 5
 см, бүйір жағының диагоналі 13
см . Параллелепипедтің табан қабырғасы мен бүйір қырын табыңыз
[3]
см, бүйір жағының диагоналі 13
см . Параллелепипедтің табан қабырғасы мен бүйір қырын табыңыз
[3]
-
Өзара параллель α және β жазықтықтар арасында орналасқан O нүктесі арқылы a және b түзулері жүргізілген: a∩α=А, a∩β =C, b∩α=B, b∩β =D және AO:AC=1:3. Егер: ОС=6см болса, АС ұзындығын табыңыз. [4]
|
Бағалау критерийлері |
№ |
Дескриптор |
Балл |
|
|
І нұсқа |
ІІнұсқа |
|||
|
Кеңістіктегі түзулердің өзара орналасуын анықтайды |
1 |
кеңістіктегі түзулердің өзара орналасуын анықтайды; |
кеңістіктегі түзулердің өзара орналасуын анықтайды; |
1 |
|
бірінші жағдай үшін суретін сызады; |
бірінші жағдай үшін суретін сызады; |
1 |
||
|
екінші жағдай үшін суретін сызады; |
екінші жағдай үшін суретін сызады; |
1 |
||
|
Параллель түзулердің қасиеттерін қолданады
|
2 |
параллель түзулердің қасиеттерін қолданады; |
параллель түзулердің анықтамасын қолданады; |
1 |
|
үшбұрыш орта сызығы қасиетін қолданады; |
параллель түзулердің қасиеттерін қолданады |
1 |
||
|
параллелограмм периметрін анықтайды; |
айқас түзулердің анықтамасын қолданады; |
1 |
||
|
қабырғаларын табады. |
айқас түзулердің қасиеттерін қолданады |
1 |
||
|
Түзу мен жазықтықтың параллельдік белгілерін және қасиеттерін қолданады |
3 |
есеп шартына сай суретін сызады; |
есеп шартына сай суретін сызады; |
1 |
|
үшбұрыштар ұқсастығын көрсетеді; |
шаршы диагоналі арқылы параллелепипедтің табан қабырғасын анықтайды |
1 |
||
|
DE кесіндісінің ұзындығын табады |
бүйір жағы диагоналі мен табанын қолданып бүйір қырын табады |
1 |
||
|
Жазықтықтардың параллельдік белгілерін қолданады
|
4 |
есеп шартына сай суретін сызады; |
есеп шартына сай суретін сызады; |
1 |
|
жазықтықтардың параллельдік белгілерін қолданады, |
жазықтықтардың параллельдік белгілерін қолданады, |
1 |
||
|
қабырғалардың пропорционалдығын құрады; |
қабырғалардың пропорционалдығын құрады; |
1 |
||
|
CN кесіндісінің ұзындығын табады. |
АС кесіндісінің ұзындығын табады. |
1 |
||
|
|
||||
|
Барлығы: |
|
|
14 |
|
«Стереометрия аксиомалары. Кеңістіктегі параллельдік»
бөлімі бойынша жиынтық бағалау нәтижелерін ата-аналарға ақпарат беру рубрикасы
Білім алушының аты-жөні: ____________________________________________________________________________
|
Бағалау критерийлері |
|
|
|
|
|
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|
|
|
|
|||||
|
|
|
Төмен |
|
|
|
|
|
Орта |
|
|
|
|
Жоғары |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Кеңістіктегі түзулердің өзара орналасуын анықтайды |
Кеңістіктегітүзулердіңөзараорналасуынанықтаудақиналады |
Параллельайқастүзулерді анықтауда қателіктер жібереді |
Кеңістіктегітүзулердіңөзара орналасуын дұрыс анықтайды |
|
|||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параллель түзулердің қасиеттерін қолданады |
Есеп |
шығаруда |
параллель |
Есеп шығаруда параллель түзулердің |
Есеп |
шығаруда |
параллель |
|
|||||||||||||
|
түзулердің |
|
қасиеттерін |
қасиеттерін |
қолдануда |
қателіктер |
түзулердің қасиеттерін |
дұрыс |
|
|||||||||||||
|
қолдануда қиналады |
|
|
|
жібереді |
|
|
|
|
|
қолданады |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Түзу мен жазықтықтың параллельдік белгілерін және қасиеттерін қолданады |
Түзу |
мен |
|
жазықтықтың |
Түзу мен жазықтықтың параллельдік |
Түзу |
мен |
|
жазықтықтың |
|
|||||||||||
|
параллельдік |
белгілерін |
және |
белгілерін |
|
және |
қасиеттерін |
параллельдік |
белгілерін |
және |
|
|||||||||||
|
қасиеттерін |
|
қолдануда |
қолдануда қателіктер жібереді |
қасиеттерін дұрыс қолданады |
|
||||||||||||||||
|
қиналады |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Жазықтықтардың параллельдік белгілерін қолданады |
Жазықтықтардың |
параллельдік |
Жазықтықтардың |
параллельдік |
Жазықтықтардың |
параллельдік |
|
||||||||||||||
|
белгілерін қолдануда қиналады |
белгілерін |
қолдануда |
қателіктер |
белгілерін дұрыс қолданады |
|
||||||||||||||||
|
|
|
|
|
|
|
|
жібереді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
«Кеңістіктегі перпендикулярлық» бөлімі бойынша жиынтық бағалау
Тақырып Түзу мен жазықтықтың перпендикулярлығы
Үш перпендикуляр туралы теорема
Кеңістіктегі арақашықтықтар
Кеңістіктегі бұрыштар
Жазықтықтардың перпендикулярлығы
Оқу мақсаттары 10.2.7 - түзу мен жазықтықтың перпендикулярлық
анықтамасын, белгісін және қасиеттерін білу, оларды
есептер шығаруда қолдану;
10.3.1 Үш перпендикуляр туралы теореманы білу
және оны есептер шығаруда қолдану
10.3.2 Түзу мен жазықтық арасындағы бұрыштың
анықтамасын білу, оның шамасын табу
10.3.3 Жазықтықтар арасындағы бұрыштың
(екіжақты бұрыш) анықтамасын білу,
кескіндей алу және оның шамасын табу
10.3.5 Нүктеден жазықтыққа дейінгі және айқас
түзулер арасындағы арақашықтықтарды таба білу
Бағалау критерийлері Білім алушы:
- Кеңістіктегі перпендикуляр, көлбеу және
көлбеудің проекциясы ұғымдарын қолданады
-үш перпендикуляр туралы теореманы қолданады
-түзу мен жазықтық арасындағы
бұрыштыкескіндейді және оның шамасын табады
-жазықтықтарарасындағыбұрышты (екіжақты
бұрыш) кескіндейді және оның шамасын табады
Ойлау дағдыларының Қолдану
деңгейі Жоғары деңгей дағдылары
Орындау уақыты 25 минут
Тапсырмалар
І нұсқа
-
Жазықтықта жатпайтын нүктеден екі көлбеу жүргізілген, олардың біреуінің ұзындығы 16 см және осы жазықтықпен
 бұрыш жасайды. Кіші көлбеудің ұзындығын табыңыз, егер оның
жазықтықтағы проекциясы 6 см. [3]
бұрыш жасайды. Кіші көлбеудің ұзындығын табыңыз, егер оның
жазықтықтағы проекциясы 6 см. [3]
-
Бір бұрышы 600 тік бұрышты үшбұрышқа сырттай сызылған шеңбердің центрінен осы үшбұрыштың жазықтығына ұзындығы 6 см тең перпендикуляр жүргізілген. Үшбұрыш жазықтығында жатпайтын перпендикулярдың бір ұшы үлкен катеттен 10 см қашықтықта орналасқан. Үшбұрыш гипотенузасының ұзындығын табыңыз. [4]
-
Ұзындығы 10 см болатын кесінді жазықтықты қиып өтеді, олардың ұштары жазықтықтан 3 см және 2см қашықтықта жатыр.Берілген кесінді және жазықтық арасындағы бұрышты табыңыз. [3]
-
Барлық қырлары өзара тең үшбұрышты пирамиданың екіжақты бұрышын табыңыз. [4]
ІI нұсқа
-
Жазықтықта жатпайтын нүктеден ұзындығы 13см және 15см екі көлбеу жүргізілген, олардың кішісінің проекциясы 5 см болса, онда екіншісінің проекциясының ұзындығын есептеңіз. [3]
-
К нүктесінен АВС үшбұрышының әрбір төбесіне дейінгі қашықтық 5см және АС=BC=5 см, ал АВ=6 см. К нүктесінен АВС жазықтығына дейінгі қашықтықты табыңыз.[4]
-
Ұзындығы 24 см болатын кесінді ұштарынан жазықтыққа дейінгі қашықтықтар сәйкесінше 43 см-ге және 31см-ге тең. Перпендикулярдың табандары арасындағы қашықтықты және кесінді мен жазықтық арасындағы бұрыштың шамасын табыңыз. [3]
-
Екі жақты бұрыштың сызықтық бұрышы 600. Осы бұрыштың қырынан A және B нүктелері алынып, оған екіжақты бұрыштың әртүрлі жақтарында жататын AC және BD перпендикулярлары түсірілген. Егер AB=6,AC=4, BD=6 болса, онда СD-ны табыңыз. [4]
|
Бағалау критерийлері |
№ |
Дескриптор |
ББалл |
|
|
І нұсқа |
ІІ нұсқа |
|||
|
Кеңістіктегі перпендикуляр, көлбеу және көлбеудің проекциясы ұғымдарын қолданады |
1 |
есеп шартына сай суретін сызады |
есеп шартына сай суретін сызады |
1 |
|
перпендикуляр ұзындығын табады |
перпендикуляр ұзындығын табады |
1 |
||
|
кіші көлбеудің ұзындығын есептейді |
үлкен көлбеудің проекциясы ұзындығын есептейді |
1 |
||
|
Үш перпендикуляр туралы теореманы қолданады |
2 |
есеп шартына сай суретін сызады |
есеп шартына сай суретін сызады |
1 |
|
үш перпендикуляр туралы теореманы қолданып үшбұрыш гипотенузасы ортасынан үлкен катетке дейін арақашықтықты табады |
үшбұрыш ауданын есептейді |
1 |
||
|
орта сызық арқылы кіші катетті анықтайды |
үшбұрышқа сырттай сызылған шеңбер радиусын есептейді |
1 |
||
|
300 қарсы жатқан катет арқылы гипотенузаны есептейді. |
биіктіқті табады |
1 |
||
|
Түзу мен жазықтық арасындағы бұрышты кескіндейді және оның шамасын табады |
3 |
түзу мен жазықтық арасындағы бұрышты кескіндейді |
есеп шартына сай суретін сызады |
1 |
|
үшбұрыштар ұқсастығын пайдаланып, кесіндінің бөлігін табады. |
арақашықтықтықты есептейді |
1 |
||
|
түзу мен жазықтық арасындағы бұрышты есептейді |
түзу мен жазықтық арасындағы бұрышты есептейді |
1 |
||
|
Жазықтықтар арасындағы бұрышты (екіжақты бұрыш) кескіндейді және оның шамасын табады |
4 |
дұрыс тетраэдр суретін кескіндейді. |
есеп шартына сай суретін сызады |
1 |
|
апофемасын есептейді |
АС=ВЕ бір жазықтықта жататын Е нүктесін белгілейді |
1 |
||
|
табан биіктігі апофемаға тең екенін және медиана қасиетін көрсетеді |
косинустар теоремасын қолданып ЕД ұзынтығын анықтайды |
1 |
||
|
екі жақты бұрышты табады |
тікбұрышты СЕД (СЕ =АВ )үшбұрышынан СД-ны табады |
1 |
||
|
Барлығы |
|
|
|
14 |
«Кеңістіктегі перпендикулярлық»
бөлімі бойынша жиынтық бағалау нәтижелерін ата аналарға ақпарат беру рубрикасы
Білім алушының аты-жөні: ______________________________________________________________________________________________
|
Бағалау критерийлері |
|
|
|
|
|
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
Төмен |
|
|
|
|
|
Орта |
|
|
|
|
|
|
Жоғары |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Кеңістіктегі перпендикуляр, |
Кеңістіктегі |
перпендикуляр, |
Кеңістіктегі |
перпендикуляр, |
көлбеу |
Кеңістіктегі |
перпендикуляр, |
|
|||||||||||||||||
|
көлбеу |
және |
көлбеудің |
және |
көлбеудің |
проекциясы |
көлбеу |
және |
көлбеудің |
|
||||||||||||||||
|
көлбеу |
жәнекөлбеудің |
|
|||||||||||||||||||||||
|
проекциясы |
|
ұғымдарын |
ұғымдарын қолданады, |
есептеулерде |
проекциясы |
ұғымдарын дұрыс |
|
||||||||||||||||||
|
проекциясы |
ұғымдарын |
|
|
||||||||||||||||||||||
|
қолдануда қиналады |
|
|
|
қателіктер жібереді |
|
|
|
|
|
қолданып, |
есепті |
дұрыс |
|
||||||||||||
|
қолданады |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шығарады |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Үш перпендикуляр |
туралы |
Үшперпендикуляр |
туралы |
Үш перпендикуляр туралы теореманы |
Үш |
перпендикуляр |
туралы |
|
|||||||||||||||||
|
теореманы қолдануда қиналады |
қолданады, |
есептеулерді |
қателіктер |
теореманы |
есеп |
шығаруда |
|
||||||||||||||||||
|
теореманы қолданады. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
жібереді |
|
|
|
|
|
|
дұрыс қолданады |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Түзу |
мен |
жазықтық |
Түзу мен жазықтық арасындағы |
Түзу |
мен |
жазықтық |
арасындағы |
Түзу мен жазықтық арасындағы |
|
||||||||||||||||
|
арасындағы |
бұрышты |
бұрышты |
|
кескіндеуде |
және |
бұрышты кескіндеуде |
және |
оның |
бұрышты кескіндейді және оның |
|
|||||||||||||||
|
кескіндейді |
және |
оның |
оның |
шамасын |
табуда |
шамасын табуда қателіктер жібереді |
шамасын дұрыс табады |
|
|||||||||||||||||
|
шамасын табады |
|
қиналады. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Жазықтықтар |
арасындағы |
Жазықтықтар арасындағы |
бұрышты |
Жазықтықтар |
арасындағы |
|
|||||||||||||||
|
Жазықтықтар |
арасындағы |
бұрышты (екіжақты бұрыш) |
(екіжақты бұрыш) кескіндеуде және |
бұрышты (екіжақты бұрыш) |
|
||||||||||||||||||||
|
бұрышты (екіжақты бұрыш) |
кескіндеуде |
|
және |
оның |
оның |
шамасын табуда |
қателіктер |
кескіндейді және оның шамасын |
|
||||||||||||||||
|
кескіндейді |
және |
оның |
шамасын табуда қиналады |
жібереді |
|
|
|
|
|
|
дұрыс табады |
|
|
|
|
|
|||||||||
|
шамасын табады |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ ТАПСЫРМАЛАРЫ
«Кеңістіктегі перпендикулярлық» бөлімі бойынша жиынтық бағалау
Тақырып Тікбұрышты параллелепипед
Жазық фигураның жазықтыққа ортогональ проекциясы және оның ауданы
Оқу мақсаттары 10.1.2 Тікбұрышты параллелепипед анықтамасын
және қасиеттерін білу
10.3.6 Жазық фигураның жазықтыққа ортогональ
проекциясы ауданының формуласын білу және оны есептер шығаруда қолдану
10.3.7 Тікбұрышты параллелепипедтің қасиеттерін
қорытып шығару және есептер шығаруда қолдану
Бағалау критерийлері Білім алушы
-
тікбұрышты параллелепипедтің анықтамасы мен қасиеттерін қолданады
-
жазық фигураның жазықтыққа ортогональ
проекциясы ауданының формуласын қолданады
Ойлау дағдыларының Қолдану
деңгейі
Орындау уақыты 20 минут
Тапсырмалар
І нұсқа
-
а)Тікбұрышты параллелепипедтің өлшемдері: 1,2; 0,9 және 2. Оның диагоналын есептеңіз. [2]
-
Тікбұрышты параллелепипедтің өлшемдері: 1:2:3 қатынасындай және оның көлемі 48см3. Тікбұрышты параллелепипедтің өлшемдерін табыңыз. [3]
-
а)Үшбұрыштың ауданы 34√2, ал оның α жазықтығындағы проекциясының ауданы 17√6. Α жазықтығы мен үшбұрыш арасындағы бұрышты табыңыз.
[3]
b) Қабырғалары а-ға және b-ға, ал олардың арасындағы сүйір бұрышы 450 –қа тең параллелограм-ромбының ортогональ проекциясы. Ромбының бір бұрышы 1200 –қа тең. Егер ромб пен параллелограм жазықтарының арасындағы бұрыш 600 болса, онда ромбының қабырғасын табыңыз.[4]
![]()
3 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ ТАПСЫРМАЛАРЫ
«Кеңістіктегі перпендикулярлық» бөлімі бойынша жиынтық бағалау
Тақырып Тікбұрышты параллелепипед
Жазық фигураның жазықтыққа ортогональ проекциясы және оның ауданы
Оқу мақсаттары 10.1.2 Тікбұрышты параллелепипед анықтамасын
және қасиеттерін білу
10.3.6 Жазық фигураның жазықтыққа ортогональ
проекциясы ауданының формуласын білу және оны есептер шығаруда қолдану
10.3.7 Тікбұрышты параллелепипедтің қасиеттерін
қорытып шығару және есептер шығаруда қолдану
Бағалау критерийлері Білім алушы
-
тікбұрышты параллелепипедтің анықтамасы мен қасиеттерін қолданады
-
жазық фигураның жазықтыққа ортогональ
проекциясы ауданының формуласын қолданады
Ойлау дағдыларының Қолдану
деңгейі
Орындау уақыты 20 минут
Тапсырмалар
ІІ нұсқа
-
а) Тікбұрышты параллелепипедтің өлшемдері: 3; 4 және 5. Оның диагоналын есептеңіз.[2]
b) Тікбұрышты параллелепипедтің өлшемдері: 0,5:1:2 қатынасындай және
оның көлемі 64см3. Тікбұрышты параллелепипедтің өлшемдерін табыңыз. [3]
2.
a)Үшбұрыштың ауданы 56 , ал оның α жазықтығындағы проекциясының ауданы
28
, ал оның α жазықтығындағы проекциясының ауданы
28 . α жазықтығы мен үшбұрыш
арасындағы бұрышты табыңыз.
. α жазықтығы мен үшбұрыш
арасындағы бұрышты табыңыз.
[3]
b)Тең бүйірлі үшбұрыштың ортогональ проекциясы – қабырғасы 6 см болатын дұрыс үшбұрыш және тең бүйірлі үшбұрыштың табаны оның проекциясының бір қабырғасымен беттеседі. Егер, осы үшбұрыштарды қамтитын жазықтықтардың арасындағы бұрыш 600 болса, онда тең бүйірлі үшбұрыштың табанына түсірілген биіктікті табыңыз. [4]
|
Бағалау критерийлері |
№ |
Дескриптор |
Балл |
|
|
І нұсқа |
ІІ нұсқа |
|||
|
Тікбұрышты параллелепипедтің қасиеттерін қолданады |
1а |
тікбұрышты параллелепипедтің диагоналының формуласын жазады |
тікбұрышты параллелепипедтің диагоналының формуласын жазады |
1 |
|
есептеулер жүргізеді |
есептеулер жүргізеді |
1 |
||
|
1b |
қатынасқа сәйкес өлшемдеріне белгілеу енгізеді |
қатынасқа сәйкес өлшемдеріне белгілеу енгізеді |
1 |
|
|
тікбұрышты параллелепипед көлемінің формуласын қолданады |
тікбұрышты параллелепипед көлемінің формуласын қолданады |
1 |
||
|
тікбұрышты параллелепипедтің өлшемдерін анықтайды |
тікбұрышты параллелепипедтің өлшемдерін анықтайды |
1 |
||
|
Жазық фигураның жазықтыққа ортогональ проекциясы ауданының формуласын қолданады |
2a |
ортогональ проекция ауданының формуласын қолданады; |
ортогональ проекция ауданының формуласын қолданады; |
1 |
|
жазық фигура мен оның ортогональ проекциясы арасындағы бұрыштың косинусын табады |
жазық фигура мен оның ортогональ проекциясы арасындағы бұрыштың косинусын табады |
1 |
||
|
косинус мәніне сәйкес бұрышты анықтайды |
косинус мәніне сәйкес бұрышты анықтайды |
1 |
||
|
2b |
шарты бойынша параллелограмм ауданын табады |
ортогональ проекция ауданының формуласын қолданады |
1 |
|
|
ромб ауданының формуласын белгісіз қабырғамен жазады |
тең қабырғалы үшбұрыш ауданын есептейді |
1 |
||
|
ромб пен параллелограмм аудандарын байланыстырып ортогональ проекция ауданының формуласын қолданады |
тең ьүйірлі үшбұрыш ауданын өрнектейді |
1 |
||
|
ромбтың қабырғасын есептейді |
тең бүйірлі үшбұрыштың табанына түсірілген биіктігін табады |
1 |
||
|
Барлығы |
|
|
|
12 |
«Кеңістіктегі перпендикулярлық»
бөлімі бойынша жиынтық бағалау нәтижелерін ата аналарға ақпарат беру рубрикасы
Білім алушының аты-жөні: ______________________________________________________________________________________________
|
Бағалау критерийлері |
|
Оқу жетістіктерінің деңгейлері |
|
||||||||||||
|
Төмен |
Орта |
Жоғары |
|||||||||||||
|
Тікбұрышты параллелепипедтің қасиеттерін қолданады |
Тікбұрышты параллелепипедтің қасиеттерін қолдануда қиналады |
Тікбұрышты параллелепипедтің қасиеттерін қолданады,есептеулердеқателіктер жібереді |
Тікбұрышты қасиеттерін Параллелепипедтің есептер шығаруда дұрыс қолданады |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Жазық фигураның жазықтыққа ортогональ проекциясы ауданының формуласын қолданады |
Жазық фигураның жазықтыққа ортогональ проекциясы ауданының формуласын қолдануда қиналады |
Жазық фигураның жазықтыққа ортогональ проекциясы қолданады, есептеулерде қателіктер жібереді |
Жазық фигураның жазықтыққа ортогональ проекциясы ауданының формуласын дұрыс қолданады |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» бөлімі бойынша жиынтық бағалау
|
Тақырып |
Кеңістіктегі векторлар және оларға амалдар қолдану. |
||
|
|
Коллинеар және компланар векторлар |
|
|
|
|
Кеңістіктегі вектордың координаталары |
|
|
|
|
Координатасымен берілген векторларды қосу және азайту, координатасымен берілген векторды санға көбейту |
|
|
|
|
Кесіндіні берілген қатынаста бөлу |
||
|
|
Кесінді ортасының координаталары |
||
|
Оқу мақсаттары |
|
||
|
|
10.4.2 - векторларды қосу және векторды санға көбейтуді орындау |
||
|
|
10.4.8 Кесіндіні берілген қатынаста бөлетін нүкте координаталарының формулаларын қорытып шығару және оларды есептер шығаруда қолдану 10.4.12 Кеңістіктегі вектордың координаталарын және ұзындығын таба білу 10.4.13 Координаталарымен берілген векторларды қосуды және векторды санға көбейтуді орындау |
||
|
|
10.4.14 Векторлардың коллинеарлық және компланарлық шартын білу және оны есептер шығаруда қолдану |
|
|
|
Бағалау критерийлері |
Білім алушы: |
|
|
-
векторды үшбұрыш ережесі бойынша қосуды орындайды
-
векторларды қосу және векторды санға көбейтуді орындайды
-
векторлардың коллинеарлық шартын қолданады
-
кеңістіктегі вектордың координаталарын және ұзындығын табады
-
кесіндіні берілген қатынаста бөлетін нүкте координаталарының формулаларын қолданады
Ойлау дағдыларының Қолдану
деңгейі Жоғары деңгей дағдылары
Орындау уақыты 25 минут
Тапсырмалар
І нұсқа
-
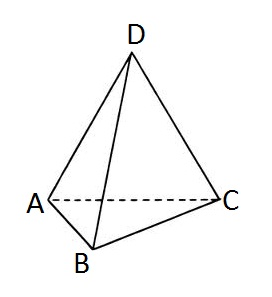
DАВС тетраэдрі берілген. Табыңдар: 1)
 2)
2)
[2]
2.
 (2;0;3),
(2;0;3),  (2;1;-4),
(2;1;-4),  (-2;1;3), векторлары
берілген.
(-2;1;3), векторлары
берілген.
 векторының координаталарын
табыңыз. [3]
векторының координаталарын
табыңыз. [3]
3.
 (2;-6;-8) және
(2;-6;-8) және
 (-1;3;-4) векторлары коллинеар болды
ма? [2]
(-1;3;-4) векторлары коллинеар болды
ма? [2]
4.
 (2;-1;3), B(0;3;5), C(-4;7;2) нүктелері
берілген.
(2;-1;3), B(0;3;5), C(-4;7;2) нүктелері
берілген.  табыңыз.[4]
табыңыз.[4]
5. DK кесіндісі берілген және оның басы болатын D1; 2; 3нүктесі белгілі.
Егер, E0;1; 2 нүктесі кесіндіні 2:1 қатынаста бөлсе, онда K нүктесінің
координаталарын табыңыз.[3]
ІІ нұсқа
-
DАВС пирамидасында 1)
 2)
2) [2]
[2] -
 ,
,  ,
,  векторлары берілген.
векторлары берілген.  векторының координаталарын табыңыз.
[3]
векторының координаталарын табыңыз.
[3] -
3.
 (3;-1;4) және
(3;-1;4) және
 (-4;
(-4; ;-4) векторлар коллинеар
болатындай a және
b
;-4) векторлар коллинеар
болатындай a және
b
шамаларының мәндерін табыңыз. [2]
-
A(2;-1;3), B(0;3;5), C(-4;7;2) нүктелері берілген табыңыз.|
 |
|
табыңыз.[4]
-
EF кесіндісі берілген және оның басы болатын Е(-1; 2; 4)нүктесі белгілі. Егер, К(0;0; 2) нүктесі кесіндіні 3:1 қатынаста бөлсе, онда F нүктесінің координаталарын табыңыз.[3]
-
Бағалау критерийлері
№
Дескриптор
Балл
Білім алушы
Векторларды ереже бойынша қосуды орындайды
1
векторларды үшбұрыш ережесі бойынша қосуды орындайды
1
векторларды азайтады
1
Векторларды координаталары бойынша қосуды және векторды санға көбейтуді көбейтуді орындайды
2
векторды санға көбейтуді орындайды
1
векторларды қосу және азайтуды орындайды
1
вектордың координатасын табады;
1
Векторлардың коллинеарлық шартын қолданады
3
коллинеарлық шартты қолданады
1
екі вектордың коллинеар екендігін анықтайды
1
Кеңістіктегі вектордың координаталарын және ұзындығын табады
3
векторларының координаталарын табады;
1
векторларға амалдар қолданады
1
вектордың ұзындығын табады;
1
Кесіндіні берілген қатынаста бөлетін нүкте координаталарының формулаларын қолданады
5
кесіндіні берілген қатынаста бөлетін нүкте координаталарының формулаларын қолданып, теңдеулер құрады
1
теңдеулерді шешеді;
1
кесінді ұшының координаталарын табады
1
Барлығы:
13
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар»
бөлімі бойынша жиынтық бағалау нәтижелерін ата-аналарға ақпарат беру рубрикасы
Білім алушының аты-жөні: _____________________________________________________________________________
|
Бағалау критерийлері |
|
|
Оқу жетістіктерінің деңгейлері |
|
|
||||||||||||||||||||||||
|
Төмен |
|
Орта |
Жоғары |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Векторларды ереже бойынша қосуды орындайды |
Векторларды ереже бойынша қосуды орындауда қиналады |
Векторларды ереже бойынша қосуды орындауда қателіктер жібереді |
Векторларды ереже бойынша қосуды дұрыс орындайды |
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
Векторлардықосужәневектордысанғакөбейтудіорындайды |
Векторлардықосужәневекторды санғакөбейтудіорындауда қиналады |
Векторларды қосужәневектордысанға көбейтудіорындаудақателіктер жібереді |
Векторлардықосужәневекторды санғакөбейтудідұрыс орындайды |
|
|
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
Векторлардың |
коллинеарлық |
Векторлардың |
коллинеарлық |
Векторлардың |
|
коллинеарлық |
Векторлардың |
коллинеарлық |
|
||||||||||||||||||||
|
шартын қолданады |
|
|
шартын қолдануда қиналады |
шартын қолданады, |
бірақ |
сұраққа |
шартын есеп шығаруда дұрыс |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
толық жауап бермейді |
|
|
|
|
қолданады |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Кеңістіктегі |
|
вектордың |
Кеңістіктегі |
|
вектордың |
Кеңістіктегі |
|
|
вектордың |
Кеңістіктегі |
|
|
вектордың |
|
|||||||||||||||
|
|
координаталарын |
|
және |
координаталарын және |
ұзындығын |
координаталарын |
|
|
және |
|
|||||||||||||||||||
|
координаталарын |
|
және |
|
|
|
|
|||||||||||||||||||||||
|
|
ұзындығын табуда қиналады |
табуда қателіктер жібереді. |
|
|
|
ұзындығын дұрыс табады. |
|
||||||||||||||||||||||
|
ұзындығын табады |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Кесіндіні |
берілген |
қатынаста |
Кесіндіні |
берілген |
|
қатынаста |
Кесіндіні берілген қатынаста бөлетін |
Кесіндіні |
берілген |
|
қатынаста |
|
|||||||||||||||||
|
бөлетін |
|
|
|
нүкте |
бөлетін |
|
|
|
нүкте |
нүкте |
|
координаталарының |
бөлетін |
|
|
|
нүкте |
|
|||||||||||
|
координаталарының |
|
координаталарының |
|
|
|
формулаларын |
қолданады,бірақ |
координаталарының |
|
|
|
|
|
||||||||||||||||
|
формулаларын қолданады |
формулаларын |
|
қолдануда |
есептеулерде қателіктер жібереді |
формулаларын дұрыс қолданады |
|
|||||||||||||||||||||||
|
|
|
|
|
|
қиналады |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
![]()
4 ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ ТАПСЫРМАЛАРЫ
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» бөлімі бойыншажиынтық бағалау
Тақырып Векторлардың скаляр көбейтіндісі
Сфера теңдеуі
Кеңістіктегі түзудің теңдеуі
Жазықтық теңдеуі
Оқыту мақсаттары 10.4.16 Координаталық түрдегі векторлардың скаляр
көбейтіндісі формуласын білу және оны
есептершығаруда қолдану
10.4.17 Кеңістіктегі екі вектордың арасындағы
бұрышты есептеу
10.4.10 Сфера теңдеуін білу және оны есептер
шығарудақолдану
10.4.18 - кеңістіктегі векторлардың перпендикулярлық
шартын білу және қолдану
10.4.20 Түзудің канондық теңдеуін құрастыру
10.4.19 Жазықтықтың жалпы теңдеуін білу, қолдану
Бағалау критерийлері Білім алушы
-
координаталық түрдегі векторлардың скаляр көбейтіндісі формуласын қолданады
-
кеңістіктегі екі вектордың арасындағы бұрышты есептейді
-
сфера теңдеуін жазады
-
түзудің канондық теңдеуін жазады
-
жазықтық теңдеуін жазады
Ойлау дағдыларының Қолдану
деңгейі Жоғары деңгей дағдылары
Орындау уақыты 25 минут
Тапсырмалар
Інұсқа
-
m-нің қандай мәнінде
 және
және  векторлары
векторлары
перпендикуляр болады ?[2]
-
а)А(1;3;0), В(2;3;-1) және С(1;2;-1) нүктелері берілген. CA және CB векторларыныңарасындағы бұрышты есептеңіз.[2]
ә)ABC тең қабырғалы үшбұрыштың қабырғасы 1-ге тең, ал MN орта сызығы
AC- ға параллель болса,
онда ![]() скаляр көбейтіндіні
табыңыз:[2]
скаляр көбейтіндіні
табыңыз:[2]
![]()
![]()
-
Сфера x² + y ² + z ² − 2x + 8y = 15 теңдеуімен берілген. Сфера центрінің координаталары мен радиусын табыңыз.[2]
-
A(2;3;-4) нүктесі арқылы өтіп,(1; −3; 5)векторына параллель болатын түзудіңканондық теңдеуін жазыңыз.[2]
-
Е(-2;1;-4)нүктесі арқылы өтетін және n=(5;-2;-3)нормаль векторы болатын жазықтық теңдеуін жазыңыз.[2]
ІІ нұсқа
-
m-нің қандай мәнінде
 және
және
 векторлары перпендикуляр
болады ?[2]
векторлары перпендикуляр
болады ?[2]
-
а)А(3;-4;1), В(1;-1;6) және С(1;-4;6) нүктелері берілген.
 және
және  векторларының арасындағы бұрышты
есептеңіз.[2]
векторларының арасындағы бұрышты
есептеңіз.[2]
b)ABC тең
қабырғалы үшбұрыштың қабырғасы 2-ге тең, ал MN орта сызығы AC- ға
параллель болса, онда  скаляр көбейтіндіні табыңыз.
скаляр көбейтіндіні табыңыз.
[2]
![]()
![]()
3. Сфера x² + y ² + z ² − 4x + 2y = 21 теңдеуімен берілген. Сфера центрінің
координаталары мен радиусын табыңыз.[2]
4. A(2;3;-4) және В(4;-2;1) нүктелері арқылы өтетін түзудіңканондық теңдеуін жазыңыз.[2]
5.Р(3;1;-2)нүктесі арқылы өтетін және n=(2;-1;-2)нормаль векторы болатын
жазықтық теңдеуін жазыңыз.[2]
|
Бағалау критерийлері |
№ |
Дескриптор |
Балл |
|
Білім алушы |
|||
|
Координаталық түрдегі векторлардың скаляр көбейтіндісі формуласын қолданады |
1 |
Координаталық түрдегі векторлардың скаляр көбейтіндісін 0-ге теңестіреді |
1 |
|
m-нің мәнін табады; |
1 |
||
|
Кеңістіктегі екі вектордың арасындағы бұрышты есептейді |
2а |
векторлардың координаталарын табады векторлардың ұзындықтарын есептейді |
1 |
|
екі вектор арасындағы бұрыш формуласын қолданады |
1 |
||
|
2b |
екі вектор арасындағы бұрышты анықтайды |
1 |
|
|
векторлардың скаляр көбейтіндісін есептейді |
1 |
||
|
Сфера теңдеуін жазады |
3 |
екімүшенің толық квадратын бөліп алады |
1 |
|
сфера центрі мен радиусын табады |
1 |
||
|
Түзудің канондық теңдеуін жазады |
4 |
түзудің канондық теңдеуінің формуласын қолданады |
1 |
|
түзудің канондық теңдеуін жазады |
1 |
||
|
Жазықтық теңдеуін жазады |
5 |
жазықтықтың нормаль вектормен берілген теңдеуі формуласын көрсетеді |
1 |
|
жазықтықтың теңдеуін жазады |
1 |
||
|
Барлығы: |
12 |
||
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар»
бөлімі бойынша жиынтық бағалау нәтижелерін ата аналарға ақпарат беру рубрикасы
Білім алушының аты-жөні: ______________________________________________________________________________________________
|
Бағалау критерийлері |
|
|
|
|
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Төмен |
|
|
|
|
|
Орта |
|
|
|
|
|
|
Жоғары |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Координаталық |
түрдегі |
Координаталық |
түрдегі |
Координаталық түрдегі векторлардың |
Координаталық |
|
түрдегі |
|||||||||||||||
|
векторлардың |
скаляр |
векторлардың |
скаляр |
скаляр |
көбейтіндісі |
формуласын |
векторлардың |
|
скаляр |
|||||||||||||
|
көбейтіндісі |
формуласын |
көбейтіндісі |
формуласын |
қолданады, |
бірақ |
есептеуде |
көбейтіндісі |
формуласын |
дұрыс |
|||||||||||||
|
қолданады |
|
қолдануда қиналады |
|
|
|
қателіктер жібереді |
|
|
|
|
қолданады |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі екі |
вектордың |
Кеңістіктегі |
екі |
вектордың |
Кеңістіктегі |
екі |
вектордың |
Кеңістіктегі |
екі |
вектордың |
||||||||||||
|
арасындағы |
бұрышты |
арасындағы |
|
бұрышты |
арасындағы |
бұрышты |
есептеуде |
арасындағы |
бұрышты |
дұрыс |
||||||||||||
|
есептейді |
|
есептеуде қиналады |
|
|
|
қателіктер жібереді |
|
|
|
|
есептейді |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сфера теңдеуін жазады |
Сфера |
теңдеуін |
қолданып |
Сфера теңдеуін қолданады, бірақ |
Сфера |
теңдеуін |
қолданып, |
|||||||||||||||
|
|
|
|
жазуда қиналады |
|
|
|
түрлендіру |
жүргізуде |
қателіктер |
теңдеуді дұрыс жазады |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
жібереді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Түзудің |
канондық теңдеуін |
Түзудің |
канондық |
теңдеуін |
Түзудің |
канондық теңдеуін |
жазуда |
Түзудің |
канондық |
теңдеуін |
||||||||||||
|
жазады |
|
|
жазуда қиналады |
|
|
|
қателіктер жібереді |
|
|
|
|
дұрыс жазады |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Жазықтық теңдеуін жазады |
|
|
Жазықтық теңдеуі формуласын жазуда қиналады |
Жазықтық теңдеуін жазуда |
|
Жазықтық теңдеуін жазады |
||||||||||||||||
|
|
|
|
|
|
қателіктер жібереді |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Жаратылыстану-математикалық бағыты
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
1-тоқсанның жиынтық бағалауына шолу
Ұзақтығы - 40минут
Балл саны - 20
Тапсырма түрлері:
ҚЖ –қысқа жауапты қажет ететін тапсырмалар; ТЖ – толық жауапты қажет ететін тапсырмалар.
Жиынтық бағалаудың құрылымы
Берілген нұсқа қысқа және толық жауапты сұрақтарды қамтитын 6 тапсырмадан тұрады.
Қысқа жауапты қажет ететін сұрақтарға білім алушылар есептелген мәні, сөздер немесе қысқа сөйлемдер түрінде жауап береді.
Толық жауапты қажет ететін сұрақтарда білім алушыдан максималды балл жинау үшін тапсырманың шешімін табудың әр қадамын анық көрсетуі талап етіледі. Білім алушының математикалық тәсілдерді таңдай алу және қолдана алу қабілеті бағаланады. Тапсырма бірнеше құрылымдық бөліктерден/сұрақтардан тұруы мүмкін.
1-тоқсан бойынша жиынтық бағалау тапсырмаларының сипаттамасы
|
Бөлім |
Тексерілетін мақсат |
Ойлау дағдыларының деңгейі |
Тапсырма саны |
№ тапсырма
|
Тапсырма түрі |
Орындау уақыты мин |
Балл
|
|
Стереометрия аксиомалары. Кеңістіктегі параллельдік |
10.2.1 - стереометрия аксиомаларын, олардың салдарларын білу; оларды кескіндеу және математикалық символдар арқылы жазып көрсету; |
Білу және түсіну |
1 |
1
|
ҚЖ
|
4
|
4
|
|
10.2.2 - кеңістіктегі параллель және айқас түзулер анықтамаларын білу, оларды анықтау және кескіндеу; |
Білу және түсіну |
1 |
2 |
ҚЖ |
3 |
2 |
|
|
10.1.1 - тетраэдр және параллелепипедтің анықтамаларын білу, тетраэдр, параллелепипедті және олардың элементтерін жазықтықта кескіндей алу; |
Білу және түсіну |
1 |
3 |
ҚЖ |
3 |
2 |
|
|
10.2.3 - кеңістіктегі параллель түзулердің қасиеттерін білу және оларды есептер шығаруда қолдану; |
Қолдану |
1 |
4 |
ТЖ |
10 |
4 |
|
|
10.2.4 - түзу мен жазықтықтың параллельдік белгісін және қасиеттерін білу, оларды есептер шығаруда қолдану |
Қолдану |
1 |
5 |
ТЖ |
10 |
4 |
|
|
10.2.5 - жазықтықтардың параллельдік белгісін және қасиеттерін білу, оларды есептер шығаруда қолдану |
Қолдану |
1 |
6 |
ТЖ |
10 |
4 |
|
|
Барлығы: |
|
6 |
|
|
40 |
20 |
|
1-тоқсанға арналған жиынтық бағалаудың тапсырмалары
І нұсқа
-
Төмендегі тұжырымдарға дұрыс немесе дұрыс емес деп жауап беріңіз.
а) Кез келген үш нүкте бір жазықтықта жатады.
[1]
b)b , A b A .
[1]
c) Bc, B c
[1]
-
Кез келген төрт нүкте бір жазықтықта жатады.
[1]
-
ABCDA1B1C1D1–текше. CD түзу өтеді.Сол түзуге параллель, текшенің төбелерінен өтетін түзулердің барлығын атаңыз.
[2]
-
DABC тетраэдрдің сызбасын салыңыз. Айқас қырлары бар ма? Егер бар болса жазып көрсетіңіз
[2]
-
A,B,C және D нүктелері бір жазықтықта жатпайды. D нүктесі арқылы AB түзуіне параллель жазықтық BC кесіндісін BK:KC=2:3 болатындай етіп K нүктесінде және AC кесіндісін E нүктесінде қиып өтеді. BC=15, AC=20. AE кесіндісі ұзындығын табыңыз .
[4]
-
Өзара параллель α және β жазықтықтар арасында орналасқан O нүктесі арқылы a және b түзулері жүргізілген: a∩α=А, a∩β =C, b∩α=B, b∩β =D және AO:AC=1:3. Егер: BO=4см болса, О D ұзындығын табыңыз
[4]
-
АВС үшбұрышының АВ қабырғасына параллель жазықтық оның АС және ВС қабырғаларымен сәйкесінше N, K нүктелерінде қиылысады. NK 2 м,
AN12 м, AC 16 м, BK 9 м екені белгілі. KC және ВС қабырғаларының ұзындықтарын табыңыз.
[4]
ІІ нұсқа
-
Мына сөйдемдерді символдарды пайдаоанып, қысқаша жазыңыз.
а) Е нүктесі а түзуіне тиісті [1]
b)b және с түзулері О нүктесінде қиылысады [1]
c)c түзуі α жазықтығында жатады [1]
d) αжазықтығы β жазықтықтығына параллель [1]
-
ABCDA1B1C1D1–текше. CC1 түзуіне айқас, текшенің төбелерінен өтетін түзулердің барлығын көрсетіңіз. [2]
-
Қыры 8см болатын DABC дұрыс тетраэдрдің сызбасын салып, апофемасын табыңыз.
[2]
-
А нүктесі- ВС кесіндісінің ортасы. А,В,С нүктелері арқылы өтетін параллель түзулер α жазықтығын сәйкесінше А1, В1, С1нүктелерінде қиып өтеді. Егер АА1=5см, ВВ1=7,5см болса. Онда СС1 ұзындығын табыңыз.
[4]
-
FEІІα, GHІІα GE
 α=O болатындай F,E, G,H нүктелері берілген. Егер GН=8cм,
FE=6см, EO=3см және HO=6см болса, онда HF пен GE кесінділерінің
ұзындығын табыңыз.
α=O болатындай F,E, G,H нүктелері берілген. Егер GН=8cм,
FE=6см, EO=3см және HO=6см болса, онда HF пен GE кесінділерінің
ұзындығын табыңыз.
[4]
-
AC және BD түзулеріSнүктесінде қиылысады. А, В және С, D нүктелері сәйкесіншепараллель және β жазықтықтарына тиісті. AS : BS= 3 : 5 , CS=12 м,BD= 30. АС жәнеSD кесінділерінің ұзындықтарын табыңыз
[4]
Балл қою кестесі
|
№ |
І нұсқа |
ІІ нұсқа |
Балл |
Қосымша ақпарат |
|
1 |
Дұрыс |
Ea |
1 |
|
|
Дұрыс емес |
b∩c=O |
1 |
||
|
Дұрыс емес |
c |
1 |
||
|
Дұрыс емес |
II β |
1 |
||
|
2 |
С |
С |
1
|
|
|
C1D1, AB, A1B1 |
AB, A1B1, AD, A1D1 |
1 |
||
|
3 |
Сызбасы
|
Сызбасы
|
1
|
|
|
AB мен CD, BC мен AD, AC мен BD |
|
1 |
||
|
4 |
BK=2x KC=3x 2x+3x=15 x=3 |
Суреті дұрыс салынған |
1 |
Балама шығару жолдары қабылданады |
|
KEIIAB AE:EC=2:3 |
СС1ВВ1 трапеция, СС1 ІІ ВВ1 |
1 |
||
|
AE= |
АА1= |
1 |
||
|
AE=8 |
СС1=2,5см |
1 |
||
|
5 |
|
Сызбасы дұрыс салынған |
1 |
Балама шығару жолдары қабылданады |
|
2AO=OC |
GHIIFE,
|
1 |
||
|
|
ΔGOH~ΔEOF |
1 |
||
|
OD=2BO OD=8 |
HF=10.5 GE=7 |
1 |
||
|
6 |
NK || AB ,ондаABC~NKC |
ASB ~CSD,
|
1 |
|
|
|
|
1 |
||
|
|
|
1 |
||
|
KC 3 BC 12 |
AC=18 |
1 |
||
|
Барлығы |
20 |
|
||
2-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
2-тоқсанның жиынтық бағалауына шолу
Ұзақтығы – 40минут
Балл саны – 20
Тапсырма түрлері:
ҚЖ –қысқа жауапты қажет ететін тапсырмалар; ТЖ – толық жауапты қажет ететін тапсырмалар.
Жиынтық бағалаудың құрылымы
Берілген нұсқа қысқа және толық жауапты сұрақтарды қамтитын 5тапсырмадантұрады.
Қысқа жауапты қажет ететін сұрақтарға білім алушылар есептелген мәні, сөздер немесе қысқа сөйлемдер түрінде жауап береді.
Толық жауапты қажет ететін сұрақтарда білім алушыдан максималды балл жинау үшін тапсырманың шешімін табудың әр қадамын анық көрсетуі талап етіледі. Білім алушының математикалық тәсілдерді таңдай алу және қолдана алу қабілеті бағаланады. Тапсырма бірнеше құрылымдық бөліктерден/сұрақтардан тұруы мүмкін.
2 тоқсандағы жиынтық бағалау тапсырмаларының сипаттамасы
|
Бөлім |
Тексерілетін мақсат |
Ойлау дағдыларының деңгейі |
Тапсырма саны |
№ тапсырма
|
Тапсырма түрі |
Орындау уақыты мин |
Балл
|
|
Кеңістіктегі перпендикулярлық |
10.2.8 - кеңістіктегі перпендикуляр, көлбеу және көлбеудің проекциясы анықтамаларын білу |
Білу және түсіну |
1 |
1
|
ҚЖ
|
3
|
3
|
|
10.2.9 - кеңістіктегі екі түзу арасындағы бұрыш анықтамасын білу |
Білу және түсіну |
1 |
2а 2b |
ҚЖ |
5 |
2 2 |
|
|
10.3.1 - үш перпендикуляр туралы теореманы білу және оны есептер шығаруда қолдану |
Қолдану |
1 |
3 |
ТЖ |
12 |
4 |
|
|
10.3.5 - нүктеден жазықтыққа дейінгі және айқас түзулер арасындағы арақашықтықтарды табу |
Қолдану |
1 |
4 |
ТЖ |
12 |
5 |
|
|
10.3.3 - жазықтықтар арасындағы бұрыштың (екіжақты бұрыш) анықтамасын білу, кескіндей алу және оның шамасын табу |
Қолдану |
1 |
5 |
ТЖ |
8 |
4 |
|
|
Барлығы: |
|
6 |
|
|
40 |
20 |
|
2-тоқсанға арналған жиынтық бағалаудың тапсырмалары
І нұсқа
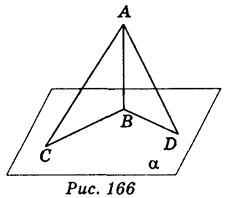
1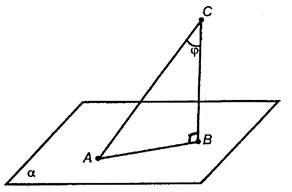 .Төменде көрсетілген суреттен көлбеу, өзінің проекциясынан екі есе
үлкен болса φ бұрышының шамасын анықтаңыз
.Төменде көрсетілген суреттен көлбеу, өзінің проекциясынан екі есе
үлкен болса φ бұрышының шамасын анықтаңыз
[3]
-
ABCDA1B1C1D1текшесі(куб)берілген.

а) AB1C бұрышының шамасын анықтаңыз
[2]
b) AС және B1D1түзулерінің арасындағы бұрышты табыңыз.
[2]
-
PQ=15 см және RS=20 см болатын екі кесіндінің ұштары өзара параллель жазықтықтарда жатады.Кіші кесіндінің жазықтықтағы проекциясының QN=9 см. Үлкен кесіндінің проекциясы SH-ты табыңыз
[4]
-
Р нүктесінен ABC үшбұрышының әрбір қабырғасына дейінгі қашықтық 5 см және AC=BC=10см, ал AB=12см.Р нүктесінен ABC жазықтығына дейінгі қашықтықты табыңыз
[5]
-
Е нүктесінен тікбұрышты екіжақты бұрыш жақтарынан 1,6 см және 1,2 см қашықтықта орналасқан. Е нүктесінен екіжақты бұрыш қырына дейінгі қашықтықты есептеңіз
[4]
2-тоқсанға арналған жиынтық бағалаудың тапсырмалары
ІІ нұсқа
-
Төменде көрсетілген суреттен -жазықтығына жүргізілген көлбеу мен оның проекциясын көрсетіңіз
[3]
.
-
ABCDA1B1C1D1текшесі(куб)берілген.

а) AА1және В1C1қырлары арасындағы бұрышшамасын анықтаңыз
[2]
b) AС жәнеAC1түзулерінің арасындағы бұрышкосинусын табыңыз.
[2]
-
ABCD квадраты жазықтығына DК перпендикуляры жүргізілген. Егер АВ=6
 м, АК=
2
м, АК=
2 болса, онда К нүктесінен АС түзуіне дейінгі қашықтықты
табыңыз[4]
болса, онда К нүктесінен АС түзуіне дейінгі қашықтықты
табыңыз[4]
-
S нүктесінен жазықтыққа екі көлбеу түсірілген,олар жазықтықты M және N нүктелерінде қияды. Көлбеулердің ұзындықтары 26 және 6√17, ал сәйкес проекцияларының қатынастары 5:3 қатынасындай. Есеп шартына сай сызбаны салып, S нүктесінен жазықтыққа дейінгі арақашықтықты табыңыз.
[5]
-
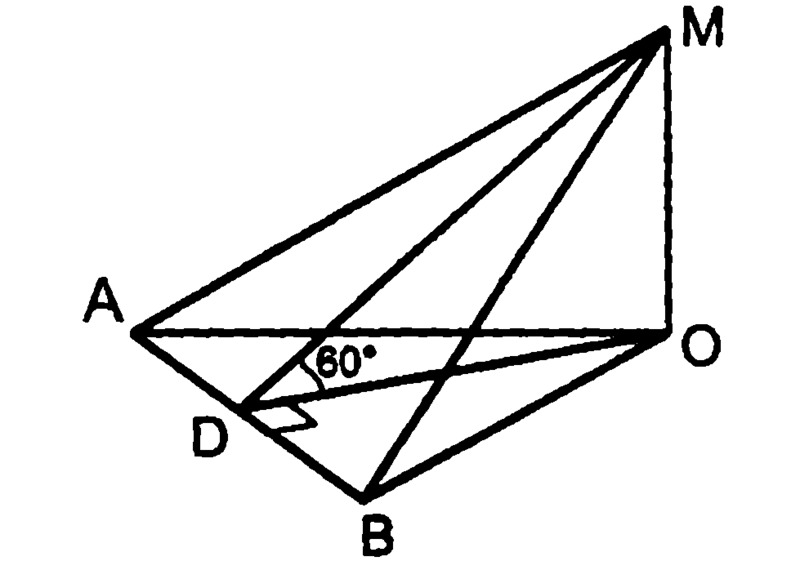
Тікбұрышты екіжақтың бұрыштың қырынан A және B нүктелері алынып, оған екіжақты бұрыштың әртүрлі жақтарында жататын AC және BD перпендикулярлары түсірілген. Егер AB=а,AC=b, BD=с болса, онда СD-ны табыңыз
[4]
Балл қою кестесі
|
№ |
І нұсқа |
ІІ нұсқа |
Балл |
Қосымша ақпарат |
|
1 |
АC=2AB |
Көлбеулер АС, АD |
1 |
|
|
sinφ= |
АСкөлбеудің проекциясы- ВС, |
1 |
||
|
φ=300 |
АDкөлбеудің проекциясы- ВD, |
1 |
||
|
2
|
Δ AB1C теңқабырғалы AB1= AC =B1C |
AА1 ІІ ВВ1 |
1 |
|
|
|
|
1 |
||
|
B1D1II BD |
АС=a |
1 |
||
|
AC |
cos(CAC1)= |
1 |
||
|
3 |
Суреті дұрыс салынған |
Суреті дұрыс салынған |
1 |
|
|
ΔPNQ, PN=12 |
Δ ADК тік бұрышты DК= |
1 |
||
|
PN=RH |
AC∩BD=O
BD=AB DO=
|
1 |
||
|
ΔRHS, SH=16 |
Δ ODК OK= |
1 |
||
|
4 |
Суреті дұрыс салынған |
Сызба дұрыс салынған |
1 |
Балама шығару жолдары қабылданады |
|
|
SH2=SM2-MH2 SH2=SN2-NH2 |
1 |
||
|
|
262-25x2=36*17-9x2 |
1 |
||
|
|
MH=10 NH=6 |
1 |
||
|
h=4 |
SH=24 |
1 |
||
|
5 |
Суреті дұрыс салынған |
Сызба дұрыс салынған |
1 |
|
|
a,b-катеттер, с -гипотенуза d-арақашықтық, d =c |
Δ ABC, BC2=AB2+AC2 |
1 |
||
|
c2=a2+b2
d= |
Δ DBC, CD2=BC2+BD2 |
1 |
||
|
d=2 |
CD= |
1 |
||
|
Барлығы |
|
20 |
|
|
3-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
3-тоқсанның жиынтық бағалауына шолу
Ұзақтығы – 40минут
Балл саны – 20
Тапсырма түрлері:
ҚЖ –қысқа жауапты қажет ететін тапсырмалар; ТЖ – толық жауапты қажет ететін тапсырмалар.
Жиынтық бағалаудың құрылымы
Берілген нұсқа қысқа жәнетолықжауаптысұрақтардықамтитын6тапсырмадантұрады.
Қысқа жауапты қажет ететін сұрақтарға білім алушылар есептелген мәні, сөздер немесе қысқа сөйлемдер түрінде жауап береді.
Толық жауапты қажет ететін сұрақтарда білім алушыдан максималды балл жинау үшін тапсырманың шешімін табудың әр қадамын анық көрсетуі талап етіледі. Білім алушының математикалық тәсілдерді таңдай алу және қолдана алу қабілеті бағаланады. Тапсырма бірнеше құрылымдық бөліктерден/сұрақтардан тұруы мүмкін.
3-тоқсан бойынша жиынтық бағалау тапсырмаларының сипаттамасы
-
Бөлім
Тексерілетін мақсат
Ойлау
дағдылар
ының
деңгейі
Тапсырма саны
№ тапсырма
Тапсырма түрі
Орындау уақыты,мин
Балл
Бөлім бойынша балл
Кеңістіктегі
перпендику
лярлық
10.1.2 - тікбұрышты параллелепипед анықтамасын және қасиеттерін білу
Білу және
түсіну
1
1
ҚЖ
3
2
6
10.3.6Жазық фигураның жазықтыққа
ортогональ проекциясы ауданының
формуласын білу және оны есептер
шығаруда қолдану
Қолдану
1
2
ТЖ
9
4
Кеңістіктегі
тікбұрышты
координата
лар жүйесі
және
векторлар
10.4.14 - векторлардың коллинеарлық және компланарлық шартын білу және оны есептер шығаруда қолдану
Қолдану
1
3
ТЖ
5
3
14
10.4.2Векторлардықосужәне
векторды санға көбейтуді орындау
Білу және түсіну
1
4
ҚЖ
4
3
10.4.7Кеңістіктегіекінүкте
арасындағы арақашықтықты табуды есептер шығаруда қолдану
Қолдану
1
5
ТЖ
9
4
10.4.12 - кеңістіктегі вектордың координаталарын және ұзындығын таба білу;
Қолдану
1
6
ТЖ
10
4
Барлығы:
6
40
20
20
3-тоқсанға арналған жиынтық бағалаудың тапсырмалары
І нұсқа
-
Қыры 5см болатын кубтың диагоналін табыңыз.
[2]
-
Үшбұрыштың ортогональ проекциясы қабырғалары 13,14,15 болатын үшбұрыш. Осы үшбұрыштар орналасқан жазықтықтар арасындағы бұрыш 600. Берілген үшбұрыштың ауданын есептеңіз.

-
 коллинеар векторлары берілген. m+n мәндерін
табыңыз.
коллинеар векторлары берілген. m+n мәндерін
табыңыз.
3]
![]()
![]()
-
Қосынды векторды табыңыз:

[3]
-
ABC үшбұрышының төбелері координаттарымен берілген: A;2;8, B1;;-1 C0; 4;.. D нүктесі– АC қабырғасының ортасы. ВD медианасының ұзындығын табыңыз.
[4]
6.
![]() ,
,
![]() ,
,
![]() ,
,
![]() нүктелерінің координаталары
берілген.
нүктелерінің координаталары
берілген. ![]() табыңыз
табыңыз
[4]
3-тоқсанға арналған жиынтық бағалаудың тапсырмалары
ІІ нұсқа
-
Диагоналі 2
 болатын кубтың қырының
ұзындығы неге тең?
болатын кубтың қырының
ұзындығы неге тең?
[2]
-
Дұрыс тетраэдрдің қыры 10см. Бүйір жағының табан жазықтығына ортогональ проекциясының ауданын табыңыз. [4]
-

 -нің қандай
мәндерінде
-нің қандай
мәндерінде  және
және  векторлары коллинеар
болады
векторлары коллинеар
болады
[3]
![]()
![]()
-
ABCD үшбұрышты пирамидасы берілген. Қосындыны табыңыз:
а) b)
b)
[3]
-
A(2;-2;6),B(2;0;-2),С(0;k;4) нүктелері берілген. k-ның қандай мәндерінде АВС тең бүйірлі үшбұрышының табаны АВ болады?
[4]
-
 ,
, 
 векторларының координаттары
берілген.
векторларының координаттары
берілген. 
 векторының ұзындығын
табыңдар.
векторының ұзындығын
табыңдар.
[4]
Балл қою кестесі
қою кестесі
|
№ |
Жауап |
|
Балл |
Қосымша ақпарат |
|
1 |
d=a |
d=a |
1 |
Тікбұрышты параллелепипед диагоналі формуласы қолдануға болады |
|
d=5 |
а=2 |
1 |
||
|
2 |
С |
|
1 |
Сызбадағы әріптердің белгіленуі, үшбұрыш ауданы басқа формуласы қолданылуы қарастырылады. |
|
Sпроекция= |
|
1 |
||
|
Sпроекция=S*cosα S=Sпр/cosα |
cosφ= |
1 |
||
|
S=84/cos600=84:1/2=168 |
|
1 |
||
|
3 |
|
|
1 |
|
|
|
|
1 |
||
|
|
|
1 |
||
|
4 |
|
Сызба дұрыс салынған |
1 |
|
|
|
|
1 |
||
|
|
|
1 |
||
|
5 |
|
AC=BC |
1 |
|
|
D(1;1;3) |
Екі нүктенің арақашықтық формуласын қолданады |
1 |
||
|
Екі нүктенің арақашықтық формуласын қолданады |
(0-2)2+(k+2)2+(4-6)2=(0-2)2+(k-0)2+(4+2)2 |
1 |
||
|
BD= |
k=7 |
1 |
||
|
6 |
|
4 |
1 |
|
|
2 |
4 |
1 |
||
|
2 |
|
1 |
||
|
|2 |
|
1 |
||
|
Барлығы |
20 |
|
||
4-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ СПЕЦИФИКАЦИЯСЫ
4-тоқсанның жиынтық бағалауына шолу
Ұзақтығы – 40минут
Балл саны – 20
Тапсырма түрлері:
ҚЖ –қысқа жауапты қажет ететін тапсырмалар; ТЖ – толық жауапты қажет ететін тапсырмалар.
Жиынтық бағалаудың құрылымы
Берілген нұсқа қысқа және толық жауапты сұрақтарды қамтитын 5 тапсырмадантұрады.
Қысқа жауапты қажет ететін сұрақтарға білім алушылар есептелген мәні, сөздер немесе қысқа сөйлемдер түрінде жауап береді.
Толық жауапты қажет ететін сұрақтарда білім алушыдан максималды балл жинау үшін тапсырманың шешімін табудың әр қадамын анық көрсетуі талап етіледі. Білім алушының математикалық тәсілдерді таңдай алу және қолдана алу қабілеті бағаланады. Тапсырма бірнеше құрылымдық бөліктерден/сұрақтардан тұруы мүмкін.
4-тоқсан бойынша жиынтық бағалау тапсырмаларының сипаттамасы
|
Бөлім |
Тексерілетін мақсат |
Ойлау дағдыларының деңгейі |
Тапсырма саны |
№ тапсырма
|
Тапсырма түрі |
Орындау уақыты мин |
Балл
|
|
Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар |
10.4.4 Кеңістіктегі векторлардың скаляр көбейтіндісінің анықтамасы мен қасиеттерін білу |
Білу және түсіну |
1 |
1 |
ҚЖ
|
6
|
4
|
|
10.4.17 Кеңістіктегі екі вектордың арасындағы бұрышты есептеу |
Қолдану |
1 |
2 |
ТЖ |
8 |
4 |
|
|
10.4.18 Кеңістіктегі векторлардың перпендикулярлық шартын білу және қолдану |
Қолдану |
1 |
3 |
ТЖ |
8 |
4 |
|
|
10.4.10 Сфера теңдеуін білу және оны есептер шығаруда қолдану |
Қолдану |
1 |
4 |
ТЖ |
9 |
4 |
|
|
10.4.21 Түзу теңдеуінің канондық түрінен параметрлік түріне көше алу |
Қолдану |
1 |
5 |
ТЖ |
9 |
4 |
|
|
Барлығы: |
|
5 |
|
|
40 |
20 |
|
4-тоқсанға арналған жиынтық бағалаудың тапсырмалары
І нұсқа
-
Егер
 және
және
 векторлар арасындағы
бұрыш
векторлар арасындағы
бұрыш  , әрі скаляр
көбейтіндісі
, әрі скаляр
көбейтіндісі  болса, онда осы векторлар
арқылы салынған параллелограмның ауданы
табыңыз
болса, онда осы векторлар
арқылы салынған параллелограмның ауданы
табыңыз
[4]
-
Үшбұрыштың төбелері A1;4;1, B5;-4;-4, C;-10;7 а)
 ,
, векторларының координаталарын табыңыз.
[2]
b)
векторларының координаталарын табыңыз.
[2]
b) және
және векторларының арасындағы бұрышты
табыңыз.[2]
векторларының арасындағы бұрышты
табыңыз.[2]
-
m-нің қандай мәнінде
 және
және  векторлары перпендикуляр болады
?
векторлары перпендикуляр болады
?
[4]
-
Сфераның теңдеуі берілген: x2y2z2 2 x 4z+6y35
-
Сфераның центрі мен радиусын табыңыз.[2]
-
A1;0;kнүктеcі сфера бетінде жататындай, k санының мәнін табыңыз
[2]
-
A5;-3;және B;1;-4нүктелері берілген.
а) AB түзуінің теңдеуін канондық түрде жазыңыз. [2]
b) AB түзуінің теңдеуін канондық түрінен параметрлік түріне көшіріңіз.
[2]
ІІ нұсқа
1.
![]() ,
,![]() векторлары600
бұрыш жасаса
және
векторлары600
бұрыш жасаса
және ,
,
 болса,
(
болса,
( ).
). скалярлық көбейтіндісін
табыңыз.[4]
скалярлық көбейтіндісін
табыңыз.[4]
2.
Үшбұрыштың төбелері A-2;;2, B3;-4;-2, C;1;2 а)  ,
, векторларының координаталарын табыңыз.
[2]
векторларының координаталарын табыңыз.
[2]
b)  және
және векторларының арасындағы бұрышты табыңыз.
[2]
векторларының арасындағы бұрышты табыңыз.
[2]
3. ![]() -нің қандай
мәнінде
-нің қандай
мәнінде ![]() және
және ![]() векторлары арасындағы бұрыш
доғал болады?
векторлары арасындағы бұрыш
доғал болады?
[4]
4. Сфераның теңдеуі берілген: x2y2z24x8z
a)Сфераның центрі мен радиусын табыңыз.[2]
b)A-2;k;7нүктеcі сфера бетінде жататындай,k санының мәнін табыңыз [2]
5. C2;-3;және D;2;3нүктелері берілген.
а) CD түзуінің теңдеуін канондық түрде жазыңыз. [2]
b) CD түзуінің теңдеуін канондық түрінен параметрлік түріне көшіріңіз.[2]
Балл қою кестесі
қою кестесі
|
№ |
І нұсқа |
ІІ нұсқа |
Балл |
Қосымша ақпарат |
|
1 |
S=|a|.|b|.sinα |
( |
1 |
Балама шығару жолы қабылданады |
|
|
|
1 |
||
|
|
|
1 |
||
|
S=1 |
( |
1 |
||
|
2 |
|
|
1 |
|
|
|
|
1 |
||
|
cosφ= |
cosφ
= |
1 |
||
|
cosφ= |
φ=450 |
1 |
||
|
3 |
|
|
1 |
|
|
|
|
1 |
||
|
|
|
1 |
||
|
m=-2 m=3 |
|
1 |
||
|
4 |
(x+1)2+(y+3)2+(z-2)2=49 |
(x+2)2+y2+(z-4)2=25 |
1 |
|
|
O(-1;-3;2) R=7 |
O(-2;0;4) R=5 |
1 |
||
|
OA2=R2 (1+1)2+(0+3)2+(k-2)2=49 |
OA2=R2 (-2+2)2+(k-0)2+(7-4)2=25 |
1 |
||
|
k=8 k=-4 |
k=-4 k=4 |
1 |
||
|
5 |
|
|
1 |
|
|
|
|
1 |
||
|
|
|
1 |
||
|
|
|
1 |
||
|
Барлығы |
|
20 |
|
|
6



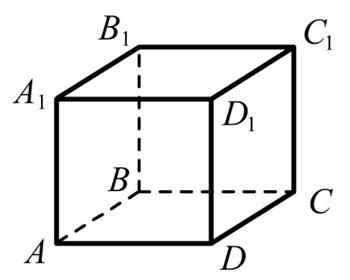 ызбасы
ызбасы



























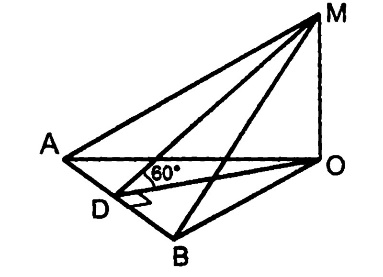 ызбасы
ызбасы
































































