
2-тоқсанға арналған жиынтық бағалаудың тапсырмалары
10 - сынып. Геометрия.
I нұсқа
-
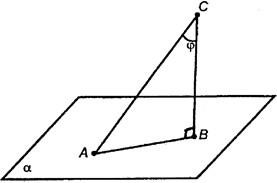
Төменде көрсетілген суреттен
 - жазықтығына
дейінгі қашықтықпен көлбеудің проекциясын атаңыз.
- жазықтығына
дейінгі қашықтықпен көлбеудің проекциясын атаңыз.
[2]
-
ABCDA1B1C1D1 текшесі (куб) берілген.
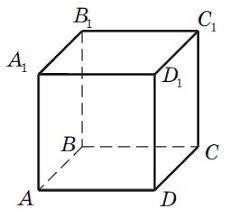
а) AВ1 және В1 С түзулерінің арасындағы бұрыш төменде көрсетілген бұрыштардың
қайсыларына тең болатынын көрсетіңіз:
 ADC1
,
ADC1
,  ВС1D
,
ВС1D
,  A1
AC1
,
A1
AC1
,  BC1D
,
BC1D
,  BDB1
,
BDB1
,  B1
AD1
B1
AD1
[2]
-
AВ1 және В1С түзулерінің арасындағы бұрышты табыңыз.
[1]
-
ABCD тіктөртбұрышының жазықтығына S нүктесінен SB перпендикуляры жүргізілген.
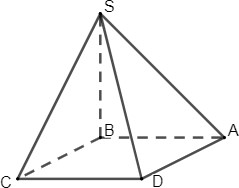
а) ASD үшбұрышы тікбұрышты екенін дәлелдеңіз. [2]
-
Егер CD = 6 см, AD = 8 см, ал SB = 10 см болса, SD түзуі мен ABC жазықтығының арасындағы бұрышты табыңыз.
[3]
-
Тікбұрышты АВС үшбұрышында АС гипотенузасы 26см,АВ :ВС =5:12 тең. Тікбұрышты
үшбұрыштың ауданын табыңыз.
[5]
-
ΔABC және ΔA1B1C1 өзара тең дұрыс үшбұрыштары сәйкесінше α, β параллель жазықтықтарында жатыр. AA1, BB1 және CC1 түзулері α жазықтығына перпендикуляр. ??1 = 3, AC=2. Есеп шартына сай сызбаны салып, ABC және А1ВС жазықтықтарының арасындағы бұрышты табыңыз.
2-тоқсанға арналған жиынтық бағалаудың тапсырмалары
10 – сынып. Геометрия
ІІ нұсқа
-
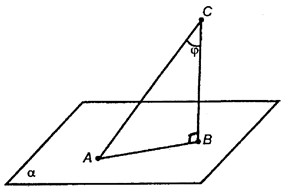
Төменде көрсетілген суреттен
 - жазықтығына жүргізілген көлбеу
мен оның проекциясын атаңыз.
- жазықтығына жүргізілген көлбеу
мен оның проекциясын атаңыз.
[2]
-
ABCDA1 B1 C 1D1 текшесі (куб) берілген.
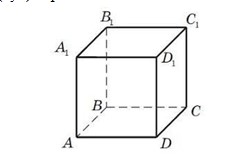
а) AD1 және DC1 түзулерінің арасындағы бұрыш төменде көрсетілген бұрыштардың қайсыларына тең болатынын көрсетіңіз:
 ADC1,
ADC1,  AD1D
,
AD1D
,  A1
AC1
,
A1
AC1
,  BC1D
,
BC1D
,  BDB1
,
BDB1
,  B1
AD1
B1
AD1
[2]
-
AD1 және DC1 түзулерінің арасындағы бұрышты табыңыз.
[1]
-
ABCD тіктөртбұрышының жазықтығына S нүктесінен SB перпендикуляры жүргізілген.
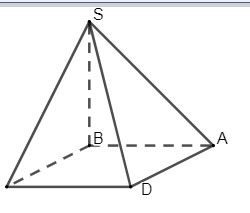
а) ASD үшбұрышы тікбұрышты екенін дәлелдеңіз. [2]
-
Егер CD = 3 см, AD = 4 см, ал SB = 5 см болса, SD түзуі мен ABC жазықтығының арасындағы бұрышты табыңыз.
[3]
4. А нүктесінен жазықтыққа екі көлбеу түсірілген, олар жазықтықты В және К нүктелерінде
қияды. Көлбеулердің ұзындықтары 26 және 6√17, ал сәйкес проекцияларының қатынастары 5:3 қатынасындай. Есеп шартына сай сызбаны салып, А нүктесінен жазықтыққа дейінгі арақашықтықты табыңыз.
[5]
5. ΔABC және ΔA1B1C1 өзара тең дұрыс үшбұрыштары сәйкесінше α, β параллель жазықтықтарында жатыр. AA1, BB1 және CC1 түзулері α жазықтығына перпендикуляр. ??1 = 3, AC=2. Есеп шартына сай сызбаны салып, ABC және А1ВС жазықтықтарының арасындағы бұрышты табыңыз.
[5]
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
10-сынып геометрия ТЖБ 2-тоқсан
10-сынып геометрия ТЖБ 2-тоқсан
2-тоқсанға арналған жиынтық бағалаудың тапсырмалары
10 - сынып. Геометрия.
I нұсқа
-
Төменде көрсетілген суреттен
 - жазықтығына
дейінгі қашықтықпен көлбеудің проекциясын атаңыз.
- жазықтығына
дейінгі қашықтықпен көлбеудің проекциясын атаңыз.

[2]
-
ABCDA1B1C1D1 текшесі (куб) берілген.

а) AВ1 және В1 С түзулерінің арасындағы бұрыш төменде көрсетілген бұрыштардың
қайсыларына тең болатынын көрсетіңіз:
 ADC1
,
ADC1
,  ВС1D
,
ВС1D
,  A1
AC1
,
A1
AC1
,  BC1D
,
BC1D
,  BDB1
,
BDB1
,  B1
AD1
B1
AD1
[2]
-
AВ1 және В1С түзулерінің арасындағы бұрышты табыңыз.
[1]
-
ABCD тіктөртбұрышының жазықтығына S нүктесінен SB перпендикуляры жүргізілген.

а) ASD үшбұрышы тікбұрышты екенін дәлелдеңіз. [2]
-
Егер CD = 6 см, AD = 8 см, ал SB = 10 см болса, SD түзуі мен ABC жазықтығының арасындағы бұрышты табыңыз.
[3]
-
Тікбұрышты АВС үшбұрышында АС гипотенузасы 26см,АВ :ВС =5:12 тең. Тікбұрышты
үшбұрыштың ауданын табыңыз.
[5]
-
ΔABC және ΔA1B1C1 өзара тең дұрыс үшбұрыштары сәйкесінше α, β параллель жазықтықтарында жатыр. AA1, BB1 және CC1 түзулері α жазықтығына перпендикуляр. ??1 = 3, AC=2. Есеп шартына сай сызбаны салып, ABC және А1ВС жазықтықтарының арасындағы бұрышты табыңыз.
2-тоқсанға арналған жиынтық бағалаудың тапсырмалары
10 – сынып. Геометрия
ІІ нұсқа
-
Төменде көрсетілген суреттен
 - жазықтығына жүргізілген көлбеу
мен оның проекциясын атаңыз.
- жазықтығына жүргізілген көлбеу
мен оның проекциясын атаңыз.

[2]
-
ABCDA1 B1 C 1D1 текшесі (куб) берілген.

а) AD1 және DC1 түзулерінің арасындағы бұрыш төменде көрсетілген бұрыштардың қайсыларына тең болатынын көрсетіңіз:
 ADC1,
ADC1,  AD1D
,
AD1D
,  A1
AC1
,
A1
AC1
,  BC1D
,
BC1D
,  BDB1
,
BDB1
,  B1
AD1
B1
AD1
[2]
-
AD1 және DC1 түзулерінің арасындағы бұрышты табыңыз.
[1]
-
ABCD тіктөртбұрышының жазықтығына S нүктесінен SB перпендикуляры жүргізілген.

а) ASD үшбұрышы тікбұрышты екенін дәлелдеңіз. [2]
-
Егер CD = 3 см, AD = 4 см, ал SB = 5 см болса, SD түзуі мен ABC жазықтығының арасындағы бұрышты табыңыз.
[3]
4. А нүктесінен жазықтыққа екі көлбеу түсірілген, олар жазықтықты В және К нүктелерінде
қияды. Көлбеулердің ұзындықтары 26 және 6√17, ал сәйкес проекцияларының қатынастары 5:3 қатынасындай. Есеп шартына сай сызбаны салып, А нүктесінен жазықтыққа дейінгі арақашықтықты табыңыз.
[5]
5. ΔABC және ΔA1B1C1 өзара тең дұрыс үшбұрыштары сәйкесінше α, β параллель жазықтықтарында жатыр. AA1, BB1 және CC1 түзулері α жазықтығына перпендикуляр. ??1 = 3, AC=2. Есеп шартына сай сызбаны салып, ABC және А1ВС жазықтықтарының арасындағы бұрышты табыңыз.
[5]

шағым қалдыра аласыз















