
10 сынып
1. 3р4+5q4+15=13p 2q2 теңдігі орындалатын p және q жай сандарын тап.
2.Дұрыс
па?  =2000;
=2000;
3. ABCD шаршысының A төбесі және CD қабырғасының ортасы l түзуіне қарағанда симметриялы. l түзуі ABCD шаршысының бөлген бөліктердің аудандарының қатнасын табыңыз.

4. 2015 санын қандай санға көбейткенде, сол санның бөлгіштерінің саны дәл 12-ге ( бір мен сол санның өзін қоса есептегенде) тең болады?
5. АВСД дөңес төртбұрышы
берілген. Сонда  , ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
, ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
6. Теңдеулер жүйесін шешіңіз:

7. Егер 2tg2α+tgα-3=0 болып π/2<α<π аралығында болса sin2α-ны тап.
10 сынып
1.![]() және
және![]() сандары бүтін сан болу үшін натурал а және
в
сандары бүтін сан болу үшін натурал а және
в
жұптарын тап.
2. 13!-11! Өрнегі 31-ге еселік екенін дәлелде.
3. а, в, с>0 болса,
 теңсіздігін дәлелде
теңсіздігін дәлелде
4.
Ықшамда:![]() ;
;
5. Дұрыс жетібұрыштың неше диагоналі бар?
6. а, в, с және x, y, z -оң нақты сандар болып, a+x=b+y=c+z=1 болса, онда
(abc+xyz) ![]() теңсіздігін дәлелде.
теңсіздігін дәлелде.
7. О центрлі шеңбердің АС және ВД хордалары К нүктесіндеқиылысады. М және Н ΔАВК және ΔСДК-ға сырттай сызылған шеңберлердіңцентрі болса, онда ОМ=КН екенін дәлелде
10 сынып
1. 3р4+5q4+15=13p 2q2теңдігі орындалатын p және q жай сандарын тап.
Шешуі : p және q тақ болса , онда сол жағы модулі 4 бойынша 3-ке тең, оң жағымодулі 4 бойынша 1-тең,бұл жағдай болмайды.Ендеше p= q=2 есеп шартына қанағаттандырылмайды p=2 болса q=3 болады, ал q=2 болса
p болмайды.
Жауабы: p= 2 ; q=3
2.Дұрыс
па?  =2000;
=2000;
 Сол жағын
түрлендіреміз:
Сол жағын
түрлендіреміз:
 =
= =
=
= =
= =2000; 2000 =
2000Жауабы:дұрыс.
=2000; 2000 =
2000Жауабы:дұрыс.
3. ABCD шаршысының A төбесі және CD қабырғасының ортасы l түзуіне қарағанда симметриялы. l түзуі ABCD шаршысының бөлген бөліктердің аудандарының қатнасын табыңыз.
Шешуі:AB=a, BN=x, DM=y деп белгілейміз.
![]()
 болғандықтан
MA=ME=a–y
болғандықтан
MA=ME=a–y
![]() тікбұрышты ұшбұрыш
сондықтан
тікбұрышты ұшбұрыш
сондықтан
![]()
![]()
![]()
![]()
![]() болғандықтан AN=EN
болғандықтан AN=EN
![]() тікбұрышты үшбұрыш сондықтан
тікбұрышты үшбұрыш сондықтан
![]()
![]() тікбұрышты үшбұрыш сондықтан
тікбұрышты үшбұрыш сондықтан
![]()
AN=EN болғандықтан
![]()
![]()
![]()
ABNM трапецияның ауданы ![]()
DMNC трапецияның ауданы ![]()
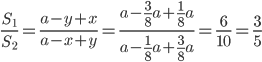 Жауабы:
Жауабы: .
.
4. 2015 санын қандай санға көбейткенде, сол санның бөлгіштерінің саны дәл 12-ге ( бір мен сол санның өзін қоса есептегенде) тең болады?
Шешуі:2015 санын көбейткіштерге жіктейміз. 2015=5·13·31
2015-тің бөлгіштері сегіз: 1, 5, 13, 31, 5·13, 5·31, 13·31, 5·13·31
Егер 2015 санын оның жай көбейткіштерінен басқа кез-келген бір жай санға көбейтсек, мысалы: 3-ке, 2015·3=3·5·13·31
2015·3санының бөлгіштері:1, 3, 5,
13, 31, ![]()
![]() бөлгіштерінің саны 15-ке тең
болады.
бөлгіштерінің саны 15-ке тең
болады.
Демек өзінің жай көбейткіштерінен басқа келкелген санға көбейткенде оның бөлгіштерінің саны 12-ден артық болады.
Енді 2015 санының жай көбейткіштеріне көбейтсек бөлгіштерінің саны дәл 12-ге тең болады.
2015·5=5·5·13·312015·5саныныңбөлгіштері: 1,5,13,31,5·5,5·13,5·31,13·31,5·5·13,5·5·31,5·13·31,5·5·13·31 саны 12-ге тең болды.
Демек, 2015 санының жай көбейткіштерінің біріне көбейтсек ол санның бөлгіштері дәл 12-ге тең болады.
Жауабы: 5, 13, 31
5. АВСД дөңес төртбұрышы
берілген. Сонда  , ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
, ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
Шешуі: А,В,С және F нүктелерінің бір шеңберге тиіс екенін дәлелдеу керек.
ΔАВF=ΔАСF =ᴪ, бұдан Δ СBL=90°-ᴪ.
6. Теңдеулер жүйесін
шешіңіз: ![]()
Шешуі:
1-ші әдісі:
![]()
![]()
![]()
Соңғы жүйедегі теңдеулерді
өзара көбейтсек:![]() болып
болып ![]() шығады. Осы теңдеуді соңғы
жүйенің бірінші теңдеуіне бөлсек
шығады. Осы теңдеуді соңғы
жүйенің бірінші теңдеуіне бөлсек
![]()
Тура осыған ұқсас жолмен
![]()
![]() шығады.
шығады.
Жауабы: ![]() және
және ![]()
2-шіәдісі:
![]()
![]()
![]()
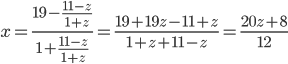

![]()
![]()
![]() теңдеуінің
шешімі
теңдеуінің
шешімі ![]() .
.
![]() теңдеуіне x-ті
қойып,
теңдеуіне x-ті
қойып, ![]()
![]() теңдеуіне z-ті
қойып,
теңдеуіне z-ті
қойып, ![]()
Жауабы: ![]() және
және ![]()
7 . Егер 2tg2α+tgα-3=0 болып π/2<α<π аралығында болса sin2α-ны тап.
Шешуі :
![]()
10 сынып
1.![]() және
және![]() сандары бүтін сан болу үшін натурал а және
в
сандары бүтін сан болу үшін натурал а және
в
жұптарын тап.
Шешуі : (2;2),(3;3),(1;2),(2;1),(2;3),(3;2).
а≥в. Егер а>в+1 болса , онда а(а-1)>в(в+1) және а 2-в>а+в 2
бұл орындалмайды.Ендеше а=в немесе а=в +1.
а=в (2;2)(3;3) болады.
Ал
а=в +1 болса , бүтін сан![]() боладыв≥6 в 2
-в-1>4в+2,
1≤в≤5 , онда тексер.
боладыв≥6 в 2
-в-1>4в+2,
1≤в≤5 , онда тексер.
2. 13!-11! Өрнегі 31-ге еселік екенін дәлелде.
Шешуі:5) 13! =1*2*3*....*13=1*2*3*....*11(12*13) =11!*12*13.
Ендеше 13!-11! =11!(12*13-1) =11!*155=11!*31*5.31-ге еселік болады.
3.
а, в, с>0 болса,
 теңсіздігін дәлелде.
теңсіздігін дәлелде.
Шешуі: Теңсіздіктің арифметикалық және гармониялық оң сан үшін қолданыпшығатыны:
 ; Бұдан кейін теңсіздікті
шеш.
; Бұдан кейін теңсіздікті
шеш.
4.
Ықшамда:![]() ;
;
Шешуі
:![]()
![]() ;
;
5. Дұрыс жетібұрыштың неше диагоналі бар?
Шешуі : Әрбір төбеден 4 диагональ жүргізуге болады, бірақ 2 диагональ үйлеседі,ендеше 14 диагональ жүргізуге болады.
Жауабы:14 диагональ.
6. а, в, с және x, y, z -оң нақты сандар болып, a+x=b+y=c+z=1 болса, онда
(abc+xyz) ![]() теңсіздігін дәлелде.
теңсіздігін дәлелде.
Шешуі :Жақшаны ашып, сол жақтың  екенін көрсетіп арықарай
екенін көрсетіп арықарай  ,мұндағы m;n>0 қолдану
жеткілікті.
,мұндағы m;n>0 қолдану
жеткілікті.
7. О центрлі шеңбердің АС және ВД хордалары К нүктесіндеқиылысады. М және Н ΔАВК және ΔСДК-ға сырттай сызылған шеңберлердіңцентрі болса, онда ОМ=КН екенін дәлелде.
Шешуі
: ОМ АВ орта перпендикуляр
болғандықтан АВ-ға , НК-ның созындысы АВ мен Р нүктесінде
қиылысады.
АВ орта перпендикуляр
болғандықтан АВ-ға , НК-ның созындысы АВ мен Р нүктесінде
қиылысады.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
10 сынып математика пәні олимпиадасы жауаптарымен І, ІІ нұсқа
10 сынып математика пәні олимпиадасы жауаптарымен І, ІІ нұсқа
10 сынып
1. 3р4+5q4+15=13p 2q2 теңдігі орындалатын p және q жай сандарын тап.
2.Дұрыс
па?  =2000;
=2000;
3. ABCD шаршысының A төбесі және CD қабырғасының ортасы l түзуіне қарағанда симметриялы. l түзуі ABCD шаршысының бөлген бөліктердің аудандарының қатнасын табыңыз.

4. 2015 санын қандай санға көбейткенде, сол санның бөлгіштерінің саны дәл 12-ге ( бір мен сол санның өзін қоса есептегенде) тең болады?
5. АВСД дөңес төртбұрышы
берілген. Сонда  , ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
, ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
6. Теңдеулер жүйесін шешіңіз:

7. Егер 2tg2α+tgα-3=0 болып π/2<α<π аралығында болса sin2α-ны тап.
10 сынып
1.![]() және
және![]() сандары бүтін сан болу үшін натурал а және
в
сандары бүтін сан болу үшін натурал а және
в
жұптарын тап.
2. 13!-11! Өрнегі 31-ге еселік екенін дәлелде.
3. а, в, с>0 болса,
 теңсіздігін дәлелде
теңсіздігін дәлелде
4.
Ықшамда:![]() ;
;
5. Дұрыс жетібұрыштың неше диагоналі бар?
6. а, в, с және x, y, z -оң нақты сандар болып, a+x=b+y=c+z=1 болса, онда
(abc+xyz) ![]() теңсіздігін дәлелде.
теңсіздігін дәлелде.
7. О центрлі шеңбердің АС және ВД хордалары К нүктесіндеқиылысады. М және Н ΔАВК және ΔСДК-ға сырттай сызылған шеңберлердіңцентрі болса, онда ОМ=КН екенін дәлелде
10 сынып
1. 3р4+5q4+15=13p 2q2теңдігі орындалатын p және q жай сандарын тап.
Шешуі : p және q тақ болса , онда сол жағы модулі 4 бойынша 3-ке тең, оң жағымодулі 4 бойынша 1-тең,бұл жағдай болмайды.Ендеше p= q=2 есеп шартына қанағаттандырылмайды p=2 болса q=3 болады, ал q=2 болса
p болмайды.
Жауабы: p= 2 ; q=3
2.Дұрыс
па?  =2000;
=2000;
 Сол жағын
түрлендіреміз:
Сол жағын
түрлендіреміз:
 =
= =
=
= =
= =2000; 2000 =
2000Жауабы:дұрыс.
=2000; 2000 =
2000Жауабы:дұрыс.
3. ABCD шаршысының A төбесі және CD қабырғасының ортасы l түзуіне қарағанда симметриялы. l түзуі ABCD шаршысының бөлген бөліктердің аудандарының қатнасын табыңыз.
Шешуі:AB=a, BN=x, DM=y деп белгілейміз.
![]()
 болғандықтан
MA=ME=a–y
болғандықтан
MA=ME=a–y
![]() тікбұрышты ұшбұрыш
сондықтан
тікбұрышты ұшбұрыш
сондықтан
![]()
![]()
![]()
![]()
![]() болғандықтан AN=EN
болғандықтан AN=EN
![]() тікбұрышты үшбұрыш сондықтан
тікбұрышты үшбұрыш сондықтан
![]()
![]() тікбұрышты үшбұрыш сондықтан
тікбұрышты үшбұрыш сондықтан
![]()
AN=EN болғандықтан
![]()
![]()
![]()
ABNM трапецияның ауданы ![]()
DMNC трапецияның ауданы ![]()
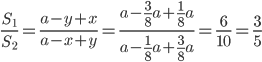 Жауабы:
Жауабы: .
.
4. 2015 санын қандай санға көбейткенде, сол санның бөлгіштерінің саны дәл 12-ге ( бір мен сол санның өзін қоса есептегенде) тең болады?
Шешуі:2015 санын көбейткіштерге жіктейміз. 2015=5·13·31
2015-тің бөлгіштері сегіз: 1, 5, 13, 31, 5·13, 5·31, 13·31, 5·13·31
Егер 2015 санын оның жай көбейткіштерінен басқа кез-келген бір жай санға көбейтсек, мысалы: 3-ке, 2015·3=3·5·13·31
2015·3санының бөлгіштері:1, 3, 5,
13, 31, ![]()
![]() бөлгіштерінің саны 15-ке тең
болады.
бөлгіштерінің саны 15-ке тең
болады.
Демек өзінің жай көбейткіштерінен басқа келкелген санға көбейткенде оның бөлгіштерінің саны 12-ден артық болады.
Енді 2015 санының жай көбейткіштеріне көбейтсек бөлгіштерінің саны дәл 12-ге тең болады.
2015·5=5·5·13·312015·5саныныңбөлгіштері: 1,5,13,31,5·5,5·13,5·31,13·31,5·5·13,5·5·31,5·13·31,5·5·13·31 саны 12-ге тең болды.
Демек, 2015 санының жай көбейткіштерінің біріне көбейтсек ол санның бөлгіштері дәл 12-ге тең болады.
Жауабы: 5, 13, 31
5. АВСД дөңес төртбұрышы
берілген. Сонда  , ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
, ал Ғ нүктесі АД кесіндінің
ортасы. ВҒ түзуі АС түзуімен Р нүктесінде қиылысады және ВС=СР
екенін дәлелде.
Шешуі: А,В,С және F нүктелерінің бір шеңберге тиіс екенін дәлелдеу керек.
ΔАВF=ΔАСF =ᴪ, бұдан Δ СBL=90°-ᴪ.
6. Теңдеулер жүйесін
шешіңіз: ![]()
Шешуі:
1-ші әдісі:
![]()
![]()
![]()
Соңғы жүйедегі теңдеулерді
өзара көбейтсек:![]() болып
болып ![]() шығады. Осы теңдеуді соңғы
жүйенің бірінші теңдеуіне бөлсек
шығады. Осы теңдеуді соңғы
жүйенің бірінші теңдеуіне бөлсек
![]()
Тура осыған ұқсас жолмен
![]()
![]() шығады.
шығады.
Жауабы: ![]() және
және ![]()
2-шіәдісі:
![]()
![]()
![]()
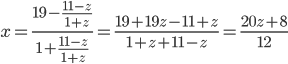

![]()
![]()
![]() теңдеуінің
шешімі
теңдеуінің
шешімі ![]() .
.
![]() теңдеуіне x-ті
қойып,
теңдеуіне x-ті
қойып, ![]()
![]() теңдеуіне z-ті
қойып,
теңдеуіне z-ті
қойып, ![]()
Жауабы: ![]() және
және ![]()
7 . Егер 2tg2α+tgα-3=0 болып π/2<α<π аралығында болса sin2α-ны тап.
Шешуі :
![]()
10 сынып
1.![]() және
және![]() сандары бүтін сан болу үшін натурал а және
в
сандары бүтін сан болу үшін натурал а және
в
жұптарын тап.
Шешуі : (2;2),(3;3),(1;2),(2;1),(2;3),(3;2).
а≥в. Егер а>в+1 болса , онда а(а-1)>в(в+1) және а 2-в>а+в 2
бұл орындалмайды.Ендеше а=в немесе а=в +1.
а=в (2;2)(3;3) болады.
Ал
а=в +1 болса , бүтін сан![]() боладыв≥6 в 2
-в-1>4в+2,
1≤в≤5 , онда тексер.
боладыв≥6 в 2
-в-1>4в+2,
1≤в≤5 , онда тексер.
2. 13!-11! Өрнегі 31-ге еселік екенін дәлелде.
Шешуі:5) 13! =1*2*3*....*13=1*2*3*....*11(12*13) =11!*12*13.
Ендеше 13!-11! =11!(12*13-1) =11!*155=11!*31*5.31-ге еселік болады.
3.
а, в, с>0 болса,
 теңсіздігін дәлелде.
теңсіздігін дәлелде.
Шешуі: Теңсіздіктің арифметикалық және гармониялық оң сан үшін қолданыпшығатыны:
 ; Бұдан кейін теңсіздікті
шеш.
; Бұдан кейін теңсіздікті
шеш.
4.
Ықшамда:![]() ;
;
Шешуі
:![]()
![]() ;
;
5. Дұрыс жетібұрыштың неше диагоналі бар?
Шешуі : Әрбір төбеден 4 диагональ жүргізуге болады, бірақ 2 диагональ үйлеседі,ендеше 14 диагональ жүргізуге болады.
Жауабы:14 диагональ.
6. а, в, с және x, y, z -оң нақты сандар болып, a+x=b+y=c+z=1 болса, онда
(abc+xyz) ![]() теңсіздігін дәлелде.
теңсіздігін дәлелде.
Шешуі :Жақшаны ашып, сол жақтың  екенін көрсетіп арықарай
екенін көрсетіп арықарай  ,мұндағы m;n>0 қолдану
жеткілікті.
,мұндағы m;n>0 қолдану
жеткілікті.
7. О центрлі шеңбердің АС және ВД хордалары К нүктесіндеқиылысады. М және Н ΔАВК және ΔСДК-ға сырттай сызылған шеңберлердіңцентрі болса, онда ОМ=КН екенін дәлелде.
Шешуі
: ОМ АВ орта перпендикуляр
болғандықтан АВ-ға , НК-ның созындысы АВ мен Р нүктесінде
қиылысады.
АВ орта перпендикуляр
болғандықтан АВ-ға , НК-ның созындысы АВ мен Р нүктесінде
қиылысады.

шағым қалдыра аласыз















