
«Геометрия» пәнінен
Жиынтық бағалауға арналғанәдістемелік ұсыныстар
10-сынып
(қоғамдық-гуманитарлық бағыты)
Нұр-Сұлтан – 2019
Әдістемелік ұсыныстар мұғалімге 10-сынып білім алушыларына «Геометрия» пәні бойынша жиынтық бағалауды жоспарлау, ұйымдастыру және өткізуге көмек құралы ретінде құрастырылған. Бөлім бойынша жиынтық бағалаудың тапсырмалары мұғалімге білім алушылардың тоқсан бойынша жоспарланған оқу мақсаттарына жету деңгейін анықтауға мүмкіндік береді.
Әдістемелік ұсыныста бөлім бойынша жиынтық бағалауды өткізуге арналған бағалау критерийі мен дескрипторлары бар тапсырмалар ұсынылған. Сондай-ақ жинақта білім алушылардың оқу жетістіктерінің мүмкін деңгейлері (рубрикалар) сипатталған. Дескрипторлары мен балдары бар тапсырмалар ұсыныс түрінде берілген.
Әдістемелік ұсыныс мұғалімдерге, мектеп әкімшілігіне, білім беру бөлімінің әдіскерлеріне, критериалды бағалау бойынша мектеп, өңірлік үйлестірушілеріне және басқа да мүдделі тұлғаларға арналған.
Әдістемелік ұсынысты дайындау барысында ресми интернет-сайттағы қолжетімді ресурстар (суреттер, фотосуреттер, мәтіндер, аудио және бейнематериалдар) қолданылды.
2
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 4
«Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы»
бөлімі бойынша жиынтық бағалау 4
2-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 8
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау 8
3-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 12
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау 12
4-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 18
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» тарауы бойынша
3
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы»
бөлімі бойынша жиынтық бағалау
Тақырып Стереометрия аксиомалары және олардың салдарлары
Кеңістіктегі екі түзудің өзара орналасуы
Түзу мен жазықтықтың өзара орналасуы
Екі жазықтықтың өзара орналасуы
Оқу мақсаты 10.2.1 Стереометрия аксиомаларын, олардың салдарларын
білу және оларды математикалық символдар арқылы
жазып көрсету
10.2.2 Кеңістіктегі параллель және айқас түзулердің
анықтамаларын білу және оларды анықтау және
кескіндеу
10.2.3 Кеңістіктегі параллель түзулердің қасиеттерін білу
және оларды есептер шығаруда қолдану
10.2.4 Түзу мен жазықтықтың параллельдік және
перпендикулярлық белгілерін, қасиеттерін білу және
оларды есептер шығаруда қолдану
10.2.5 Жазықтықтардың параллельдігі мен
перпендикулярлығының белгілерін білу және
оларды есептер шығаруда қолдану
Бағалау критерийі Білім алушы
Стеореметрия аксиомаларын және олардың салдарын
қолданады
Кеңістіктегі түзулердің өзара орналасуын анықтайды
Түзу мен жазықтықтың параллельдік белгісін
қолданады
Жазықтықтардың параллельдік қасиетін қолданады
Ойлау дағдыларының Қолдану
деңгейі
Орындау уақыты 25 минут
Тапсырма
-
Берілген символдық жазу бойынша сызбаны салып, дәлелдеңіз:
( ∩ )= , ∈ , ∉ ⇨ ⊄
-
Төменде АВСDA1B1C1D1 текшесінің суреті берілген. Келесі түзулер жұбының орналасуын анықтаңыз:
-
QP және AD1, мұндағы Q және Р сәйкесінше DD1 және AD кесінділерінің орталары;
-
-
AD1 және A1P;
-
MN және AD1, мұндағы M және N сәйкесінше A1B1 және BB1 кесінділеріне тиісті;
-
CD және A1 P;
-
MN және AB?
Қиылысатын түзулер үшін қиылысу нүктесін анықтаңыз, ал айқас және параллель түзулер үшін сәйкес белгіні қолданып жазыңыз.
4
-
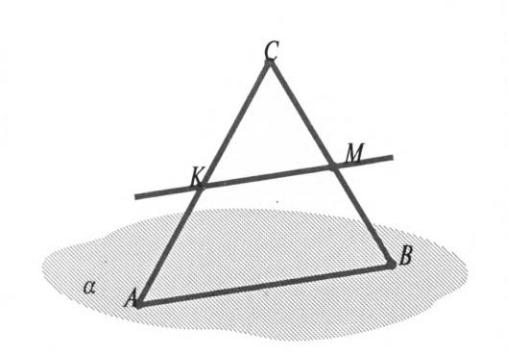
АВ кесіндісі 15 см-ге тең және α жазықтығында жатыр. С нүктесі α жазықтығына тиісті емес. К және М нүктелері сәйкесінше АС мен ВС кесінділерінің орталары.
а) КМ түзуінің α жазықтығымен ортақ нүктелері болуы мүмкін бе? Жауабыңызды негіздеңіз.
-
К және М нүктелерінің арақашықтығы неге тең?
-
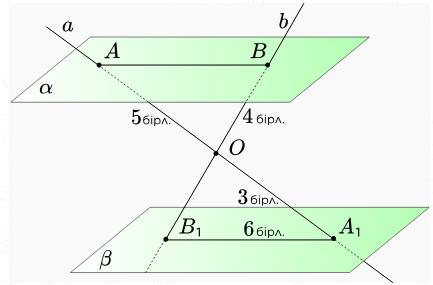
a және b түзулері О нүктесінде қиылысады. Олар және параллель жазықтықтарын суретте көрсетілгендей, А, А1, В, В1 нүктелерінде қияды. АВ және ОВ1 ұзындықтарын табыңыз.
5
|
Бағалау критерийі |
Тапсырма |
|
|
Дескриптор |
|
Балл |
||
|
№ |
Білім алушы |
|
||||||
|
|
|
|
|
|
||||
|
Стеореметрия |
|
|
қиылысушы жазықтықтарды салады; |
1 |
||||
|
аксиомаларын |
және |
1 |
сызбада PQ-дің β-ны қиғаны көрінеді; |
1 |
||||
|
олардың |
|
салдарын |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
аксиомаларды/салдарларды |
қолданып |
|
|||||
|
қолданады |
|
|
|
1 |
||||
|
|
|
|
тұжырым жасайды; |
|
||||
|
|
|
|
|
|
|
|||
|
Кеңістіктегі түзулердің |
|
параллель түзулерді анықтайды; |
1 |
|||||
|
өзара |
орналасуын |
|
параллель түзулердің белгісін жазады; |
1 |
||||
|
анықтайды |
|
|
|
қиылысатын түзулерді табады; |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
қиылысатын |
түзулердің |
қиылысу |
1 |
|
|
|
|
|
|
нүктелерін табады; |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
айқас түзулерді табады; |
|
1 |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
айқас түзулердің белгісін жазады; |
1 |
|||
|
|
|
|
|
|||||
|
Түзу мен жазықтықтың |
|
түзулердің параллельділігін анықтайды; |
1 |
|||||
|
параллельдік |
белгісін |
3 |
түзу |
мен |
жазықтықтың параллельдік |
1 |
||
|
қолданады |
|
|
белгісін қолданады; |
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
ұзындықты анықтайды; |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Жазықтықтардың |
|
параллель |
жазықтықтардың |
қасиетін |
1 |
|||
|
параллельдік |
қасиетін |
|
қолданады; |
|
|
|||
|
|
|
|
|
|||||
|
қолданады |
|
|
4 |
үшбұрыштардың ұқсастығын |
анықтап, |
|
||
|
|
|
|
сәйкес |
қабырғалардың |
қатынасын |
1 |
||
|
|
|
|
|
|||||
|
|
|
|
|
жазады; |
|
|
|
|
|
|
|
|
|
белгісізді табады. |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
Барлығы: |
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
6
Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ______________________________________________________
|
|
Бағалау критерийі |
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|||||
|
|
|
|
|
Төмен |
Орта |
|
|
|
Жоғары |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
Стеореметрия |
аксиомаларын |
Стереометрия |
аксиомаларын, |
Стереометрия |
|
|
Стереометрия |
аксиомаларын, |
|||||
|
және |
олардың |
салдарын |
олардың |
|
салдарларын |
аксиомаларын, |
олардың |
|
олардың |
|
салдарларын, |
||
|
қолданады |
|
қолдануда қиналады. |
салдарларын |
|
қолдануда |
|
математикалық символикасын |
||||||
|
|
|
|
|
|
|
қателіктер жібереді. |
|
дұрыс қолданады. |
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
Кеңістіктегі түзулердің өзара |
Кеңістіктегі |
түзулердің өзара |
Кеңістіктегі |
|
параллель/ |
|
Кеңістіктегі түзулердің өзара |
||||||
|
орналасуын анықтайды |
орналасуын |
анықтауда |
айқас/ қиылысатын түзулерді |
|
орналасуын |
|
дұрыс |
||||||
|
|
|
|
қиналады. |
|
анықтауда |
|
қателіктер |
|
анықтайды. |
|
|
||
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Түзу |
мен |
жазықтықтың |
Түзу |
мен |
жазықтықтың |
Түзумен |
жазықтықтың |
|
Түзу |
мен |
жазықтықтың |
||
|
параллельдік |
белгісін |
параллельдік |
белгісін |
параллельдік |
|
белгісін |
|
параллельдік |
белгісін |
дұрыс |
|||
|
қолданады |
|
қолдануда қиналады. |
қолданады, |
бірақ |
жауапты |
|
қолданады. |
|
|
||||
|
|
|
|
|
|
|
негіздеуде |
|
қателіктер |
|
|
|
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Жазықтықтардың |
параллельдік |
Жазықтықтардың параллельдік |
Жазықтықтардың |
|
|
Жазықтықтардың |
|
||||||
|
қасиетін қолданады |
қасиетін қолдануда қиналады. |
параллельдік |
|
қасиетін |
|
параллельдік |
қасиетін |
||||||
|
|
|
|
|
|
|
қолданады, |
|
бірақ |
|
қолданып, |
есепті |
дұрыс |
|
|
|
|
|
|
|
|
есептеулерде |
|
қателіктер |
|
шығарады. |
|
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау
Тақырып
Кеңістіктегі түзулер арасындағы бұрыш
Перпендикуляр және көлбеу
Үш перпендикуляр туралы теорема
Оқу мақсаты
10.2.6 Кеңістіктегі екі түзу арасындағы бұрыш
анықтамасын білу
10.3.5 Кеңістіктегі перпендикуляр, көлбеу және
көлбеудің проекциясы анықтамаларын білу
10.3.1 Үш перпендикуляр туралы теореманы білу және
оны есептер шығаруда қолдану
Бағалау критерийі
Білім алушы
Кеңістіктегі екі түзу арасындағы бұрышты
табады
Ойлау дағдыларының
деңгейлері
Орындау уақыты
Кеңістіктегі перпендикуляр, көлбеу және
көлбеудің проекциясы анықтамаларын қолданады
Үш перпендикуляр туралы теореманы
қолданады
Қолдану
25 минут
Тапсырма
-
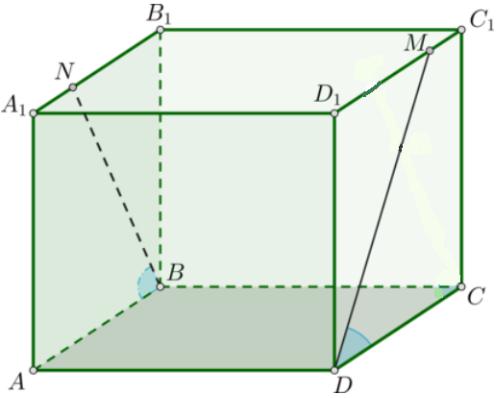
ABCDA1B1C1D1 - текше. A1B1 және C1D1 қырларында сәйкесінше N және M
нүктелері берілген, MDC NBA 600 . NB және MD кесінділері арасындағы бұрышты табыңыз.
-
M нүктесінен жазықтығына MA, MB көлбеулері және MO перпендикуляры жүргізілген.
-
көлбеулердің жазықтығына проекциясын салыңыз;
b) егер = 600, = 450, = 16 см болса, проекциялардың ұзындығын табыңыз.
-
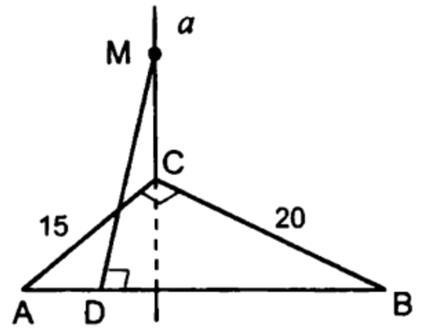
a түзуі ABC жазықтығына перпендикуляр, MD 13 см, АС=15см, ВС=20см. АВС үшбұрышы тікбұрышты: = 900.
MC кесіндісінің ұзындығын табыңыз.
9
|
Бағалау критерийі |
Тапсырма |
|
Дескриптор |
|
Балл |
||
|
№ |
|
Білім алушы |
|
||||
|
|
|
|
|
|
|
||
|
Кеңістіктегі |
екі түзу |
|
NB немесе MD түзуін екінші түзумен |
1 |
|||
|
арасындағы |
бұрышты |
1 |
қиылысқанша параллель көшіреді; |
|
|||
|
табады |
|
|
|
|
|
|
|
|
|
|
NB және MD кесінділері арасындағы |
1 |
||||
|
|
|
|
|||||
|
|
|
|
|
бұрышты анықтайды; |
|
|
|
|
Кеңістіктегі |
|
2a |
көлбеулердің проекцияларын салады |
1 |
|||
|
перпендикуляр, көлбеу |
|
бұрыштың |
тангенсінің |
анықтамасын |
1 |
||
|
және |
|
көлбеудің |
|
қолданады; |
|
||
|
|
|
|
|
||||
|
проекциясы |
|
2b |
теңбүйірлі |
тікбұрышты |
үшбұрыштың |
1 |
|
|
анықтамаларын |
|
қасиетін қолданады; |
|
||||
|
|
|
|
|||||
|
қолданады |
|
|
проекциялардың ұзындықтарын табады; |
1 |
|||
|
|
|
|
|
|
|
|
|
|
Үш |
перпендикуляр |
|
∆ABC |
тікбұрышты |
үшбұрышына |
1 |
|
|
туралы |
|
теореманы |
|
Пифагор теоремасын қолданады; |
|||
|
|
|
|
|||||
|
қолданады |
|
|
гипотенуза ұзындығын есептейді; |
1 |
|||
|
|
|
|
|
|
|
||
|
|
|
|
3 |
үш перпендикуляр туралы теореманы |
1 |
||
|
|
|
|
қолданады; |
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
үшбұрыштың тік бұрышынан түсірілген |
1 |
||
|
|
|
|
|
биіктіктің ұзындығын табады; |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
ізделінді кесінді ұзындығын табады; |
1 |
||
|
|
|
|
|
|
|
|
|
|
Барлығы: |
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
10
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ___________________________________________
|
Бағалау критерийі |
|
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|
|||||||||
|
|
|
|
Төмен |
|
|
|
Орта |
|
|
|
|
|
Жоғары |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Кеңістіктегі екі |
түзу |
Кеңістіктегі |
|
екі |
Кеңістіктегі екі |
түзу |
Кеңістіктегі |
екітүзу |
||||||||||
|
арасындағы |
|
түзу |
арасындағы |
арасындағы |
|
|
|
|
арасындағы |
|
бұрышты |
|||||||
|
бұрышты табады |
бұрышты |
табуда |
бұрышты |
табуда |
дұрыс табады. |
|
|
|
|
|||||||||
|
|
|
|
қиналады. |
|
|
|
қателіктер жібереді. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
|
Кеңістіктегі |
|
|
|
Кеңістіктегі |
|
|
|
|
Кеңістіктегі |
|
|
|
|
|||
|
перпендикуляр, |
|
перпендикуляр, |
перпендикуляр |
/ |
|
перпендикуляр, |
көлбеу |
|||||||||||
|
көлбеу |
|
және |
көлбеу |
|
және |
көлбеу |
|
|
|
|
және |
|
көлбеудің |
|||||
|
көлбеудің |
|
|
көлбеудің |
|
|
|
анықтамаларын |
|
|
|
проекциясы |
|
|
|
|
|||
|
проекциясы |
|
проекциясы |
|
|
|
қолданады, |
|
бірақ |
анықтамаларын |
дұрыс |
||||||||
|
анықтамаларын |
|
анықтамаларын |
көлбеудің |
|
|
|
|
қолданады. |
|
|
|
|
||||||
|
қолданады |
|
|
қолдануда |
|
|
|
проекциясын |
табуда |
|
|
|
|
|
|
||||
|
|
|
|
қиналады. |
|
|
|
қателіктер жібереді. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Үш перпендикуляр |
Үш перпендикуляр |
Үш перпендикуляр |
Үш |
перпендикуляр |
||||||||||||||
|
туралы |
теореманы |
туралы |
теореманы |
туралытеореманы |
туралы теореманы дұрыс |
|||||||||||||
|
қолданады |
|
|
қолдануда |
|
|
|
қолданады, |
|
|
|
|
қолданып, |
|
есептің |
||||
|
|
|
|
қиналады. |
|
|
|
есептеулер |
|
|
|
|
шешімін дұрыс табады. |
||||||
|
|
|
|
|
|
|
|
|
жүргізуде қателіктер |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
3-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау
|
Тақырып |
|
Түзу мен жазықтық арасындағы бұрыш |
|
|||
|
|
|
Екі жазықтық арасындағы бұрыш. Екіжақты бұрыш |
||||
|
|
|
Кеңістіктегі арақашықтық |
|
|
||
|
Оқу мақсаты |
10.3.2 Түзу мен |
жазықтық |
арасындағы |
бұрыштың |
||
|
|
|
|
анықтамасын білу, кескіндей алу және оның |
|||
|
|
|
|
шамасын табу |
|
|
|
|
|
|
10.3.3 Жазықтықтар |
арасындағы бұрыштың |
(екіжақты |
||
|
|
|
|
бұрыш) анықтамасын білу, кескіндей алу және |
|||
|
|
|
|
оның шамасын табу |
|
|
|
|
|
|
10.3.4 Нүктеден жазықтыққа дейінгі және айқас түзулер |
||||
|
|
|
|
арасындағы арақашықтықтарды таба білу |
|||
|
Бағалау критерийі |
Білім алушы |
|
|
|
||
|
|
|
|
Түзу мен жазықтық арасындағы бұрыштың |
|||
|
|
|
шамасын табады |
|
|
|
|
|
|
|
|
Жазықтықтар арасындағы бұрыштың (екіжақты |
|||
|
|
|
бұрыш) шамасын табады |
|
|
||
|
|
|
|
Нүктеден жазықтыққа |
дейінгі арақашықтықты |
||
|
|
|
табады |
|
|
|
|
|
Ойлау |
дағдыларының |
Қолдану |
|
|
|
|
|
деңгейлері |
|
|
|
|
|
|
|
Орындау уақыты |
25 минут |
|
|
|
||
Тапсырма
-
ABCDA' B'C' D' бірлік текшесі (куб).
а) ABC жазықтығы мен AC' түзуі арасындағы бұрыштың косинусын табыңыз;
-
егер M нүктесі AB қырының ортасы болса, онда MA’D және CA’D жазықтықтарының арасындағы бұрыштың косинусын табыңыз.
-
А нүктесінен жазықтығына ұзындығы 17 см болатын көлбеу жүргізілген. Осы көлбеудің жазықтығындағы проекциясы 15 см-ге тең.
Есептің шарты бойынша сызбаны салыңыз және А нүктесінен жазықтығына дейінгі қашықтықты табыңыз.
12
|
Бағалау критерийі |
Тапсырма |
|
|
Дескриптор |
|
Балл |
|||
|
№ |
Білім алушы |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
түзу мен жазықтық арасындағы бұрышты |
1 |
|||||
|
|
|
|
кескіндейді; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
Түзу мен жазықтықтың |
|
кубтың диагоналін есептейді; |
|
1 |
|||||
|
арасындағы бұрыштың |
1а |
тікбұрышты |
үшбұрыштағы қатынасты |
1 |
|||||
|
шамасын табады. |
|
қолданады; |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
түзу |
мен |
жазықтық |
арасындағы |
1 |
||
|
|
|
|
бұрыштың косинусын табады; |
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
сызбаны салады; |
|
|
|
1 |
||
|
|
|
|
МA1D және CA1D жазықтықтары A1D |
1 |
|||||
|
|
|
|
түзуі |
бойымен |
қиылысатынын |
||||
|
|
|
|
анықтайды; |
|
|
|
|
|
|
|
Жазықтықтар |
|
MA1D |
теңбүйірліүшбұрышының |
|
|||||
|
|
медианасы |
A1D -ға |
перпендикуляр |
1 |
|||||
|
арасындағы бұрыштың |
1b |
болатынын көрсетеді; |
|
|
|
||||
|
(екіжақты |
бұрыш) |
|
|
|
|||||
|
|
MA1D |
және |
|
CA1D |
жазықтықтары |
|
|||
|
шамасын табады |
|
|
|
||||||
|
|
арасындағы |
|
екіжақты |
бұрышты |
1 |
||||
|
|
|
|
|
||||||
|
|
|
|
анықтайды; |
|
|
|
|
|
|
|
|
|
|
тікбұрышты үшбұрыштағы сүйір бұрыш |
1 |
|||||
|
|
|
|
тангенсінің анықтамасын қолданады; |
||||||
|
|
|
|
|
||||||
|
|
|
|
жазықтықтардың |
арасындағы |
бұрышты |
1 |
|||
|
|
|
|
табады; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Нүктеден |
жазықтыққа |
|
сызбаны салады; |
|
|
|
1 |
||
|
дейінгі |
|
|
|
|
|
|
|
|
|
|
|
|
Анүктесінен |
жазықтыққа |
дейінгі |
1 |
||||
|
арақашықтықты |
2 |
||||||||
|
қашықтықты сызбада көрсетеді; |
|
||||||||
|
|
|
||||||||
|
табады |
|
|
|
|
|
|
|
|
|
|
|
|
нүктеден |
жазықтыққа |
дейінгі |
1 |
||||
|
|
|
|
|||||||
|
|
|
|
қашықтықты анықтайды; |
|
|
||||
|
|
|
|
|
|
|
||||
|
Барлығы: |
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
13
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ___________________________________________
|
Бағалау критерийі |
|
Оқу жетістіктерінің деңгейлері |
|
|
||||
|
|
|
Төмен |
Орта |
|
Жоғары |
|||
|
|
|
|
|
|
|
|
|
|
|
Түзу мен жазықтық |
Түзу мен жазықтық |
Түзу мен |
жазықтық |
Түзу |
мен |
жазықтық |
||
|
арасындағы |
|
арасындағы |
арасындағы |
бұрыштың |
||||
|
арасындағы |
|
|
||||||
|
|
бұрыштың |
|
бұрыштың |
шамасын |
шамасын дұрыс табады. |
|||
|
бұрыштың |
шамасын |
|
||||||
|
шамасын |
табуда |
табуда |
қателіктер |
|
|
|
||
|
табады. |
|
|
|
|
||||
|
|
қиналады. |
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
Жазықтықтар |
Жазықтықтар |
Жазықтықтар |
Жазықтықтар |
|
||||
|
арасындағы |
|
арасындағы |
|
арасындағы |
арасындағы |
бұрыштың |
||
|
бұрыштың (екіжақты |
бұрыштың |
|
бұрышты |
(екіжақты |
(екіжақты |
бұрыш) |
||
|
бұрыш) |
шамасын |
(екіжақты |
бұрыш) |
бұрыш) анықтайды, |
шамасын дұрыс табады. |
|||
|
табады. |
|
шамасын |
табуда |
бұрыштың |
шамасын |
|
|
|
|
|
|
қиналады. |
|
табуда |
қателіктер |
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нүктеден |
|
Нүктеден |
|
Нүктеден |
|
Нүктеден |
жазықтыққа |
|
|
жазықтыққа |
дейінгі |
жазықтыққа дейінгі |
жазықтыққа дейінгі |
дейінгі |
арақашықтықты |
|||
|
арақашықтықты |
арақашықтықты |
арақашықтықты |
дұрыс табады. |
|||||
|
табады. |
|
табуда қиналады. |
табуда |
қателіктер |
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
14
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» бөлімі бойынша жиынтық бағалау
|
Тақырып |
|
|
|
|
|
Кеңістіктегі тікбұрышты координаталар жүйесі |
|||||||||||||
|
|
|
|
|
|
|
|
Екі нүктенің арақашықтығы |
|
|
||||||||||
|
|
|
|
|
|
|
|
Кесінді ортасының координаталары |
|
|||||||||||
|
|
|
|
|
|
|
|
Сфера теңдеуі |
|
|
|
|||||||||
|
Оқу мақсаты |
|
|
|
|
|
10.4.1 Кеңістіктегі |
тікбұрышты |
координаталар жүйесін |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
жазықтықта кескіндей алу және оны сипаттау |
|||||||
|
|
|
|
|
|
|
|
10.4.2 Кеңістіктегі екі нүкте арасындағы арақашықтықты |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
таба білу |
|
|
|
||||
|
|
|
|
|
|
|
|
10.4.3 Кеңістіктегі |
кесінді ортасының |
координаталарын |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
таба білу |
|
|
|
||||
|
|
|
|
|
|
|
|
10.4.4 Сфера теңдеуін білу және оны есептер шығаруда |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
қолдану |
|
|
|
||||
|
Бағалау критерийі |
|
|
|
|
Білім алушы |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
тікбұрышты |
координаталар |
||||
|
|
|
|
|
|
|
|
|
|
|
жүйесінде нүктелерді кескіндейді және нүктелердің |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
координаталарын табады. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
екі |
нүкте |
арасындағы |
|||
|
|
|
|
|
|
|
|
|
|
|
арақашықтықты табады |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сфера теңдеуін түрлендіреді |
|
|||||
|
Ойлау |
дағдыларының |
Қолдану |
|
|
|
||||||||||||||
|
деңгейлері |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Орындау уақыты |
|
|
|
|
|
25 минут |
|
|
|
||||||||||
|
Тапсырма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1. a) |
Кеңістікте |
C |
3; |
|
; |
5 |
|
3 нүктесі берілген. С нүктесінің Oxy; Oxz; Oyz |
|||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
![]()
![]()
![]()
![]()
жазықтықтарындағы және Ox; Oy; Oz осьтеріндегі проекциясының координаталарын табыңыз.
-
Тікбұрышты координаталар жүйесінде келесі нүктелерді салыңыз:
A(1;2;3), B(2;0;1), C(0;0;3), D(3; 2;0)
-
ABC үшбұрышы берілген, мұндағы A(1; 3; 2), B(0; 2; 4), C(1; 1; 4).
Егер А1 нүктесі ВС қабырғасының ортасы болса, онда АА1 кесіндісінің ұзындығын табыңыз.
3. Сфера x2 y2 z 2 4x 8z 5 теңдеуімен берілген. A1; m; 4 нүктеcі сфераның
бойында орналасқан.
a) сфера центрінің координаталары мен оның радиусын табыңыз.
b) m – нің мәнін табыңыз.
15
|
Бағалау критерийі |
Тапсырма |
|
Дескриптор |
|
|
Балл |
||||
|
№ |
Білім алушы |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
Кеңістіктегі |
|
|
Oxy жазықтығына тиісті нүктені табады; |
1 |
||||||
|
|
|
Oxz және Oyz |
жазықтықтарына |
тиісті |
1 |
|||||
|
тікбұрышты |
|
|
||||||||
|
|
1a |
нүктелерді табады; |
|
|
|
|
||||
|
координаталар |
|
|
|
|
|
|||||
|
|
Ox; Oy; |
Oz осьтеріне тиісті |
нүктелерді |
|
||||||
|
жүйесінде |
нүктелерді |
|
1 |
|||||||
|
|
табады ; |
|
|
|
|
|
|
|||
|
кескіндейді |
және |
|
|
|
|
|
|
|
|
|
|
|
тікбұрышты |
координаталар |
жүйесін |
|
||||||
|
нүктелердің |
|
|
1 |
|||||||
|
|
|
салады; |
|
|
|
|
|
|
||
|
координаталарын |
1b |
|
|
|
|
|
|
|
||
|
берілген |
нүктелерді |
координаталар |
|
|||||||
|
табады. |
|
|
1 |
|||||||
|
|
|
жүйесінде салады. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
Кеңістіктегі |
кесінді |
|
ВС |
кесіндісінің |
|
ортасының |
1 |
|||
|
|
координаттарын анықтайды; |
|
|
|||||||
|
|
|
|
|
|||||||
|
ортасының |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Кесіндісінің |
ұзындығын |
анықтау |
1 |
|||||
|
координаталарын |
||||||||||
|
|
формуласын қолданады; |
|
|
|
||||||
|
табады. |
|
|
|
|
|
|
||||
|
|
|
АА1 кесіндісінің ұзындығын анықтайды; |
1 |
|||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
толық |
квадратты |
бөліп |
алу |
тәсілін |
1 |
||
|
|
|
|
қолданады; |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
Сфераның |
теңдеуін |
3a |
түрлендірулерді орындайды; |
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
||
|
түрлендіреді. |
|
шеңбер |
центрінің |
координаталары мен |
1 |
|||||
|
|
|
|
радиусын табады; |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
3b |
А нүктесіне сәйкес теңдеуді шешеді; |
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
белгісіз айнымалының мәнін табады; |
1 |
|||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Барлығы: |
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
16
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ___________________________________________
|
Бағалау критерийі |
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|||||||
|
|
|
Төмен |
|
|
Орта |
|
Жоғары |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
|
|
Кеңістіктегі |
|
|
|
Кеңістіктегі |
|
|
|
|
|
Кеңістіктегі |
|
тікбұрышты |
|
|
тікбұрышты |
|
|
|
тікбұрышты |
|
|
|
|
|
тікбұрышты |
|
координаталар |
|
|
координаталар |
координаталар |
|||||||
|
координаталар |
жүйесінде |
|
|
жүйесінде |
нүктелерді |
жүйесінде |
нүктелерді |
||||||
|
жүйесінде нүктелерді |
нүктелерді |
|
|
кескіндеуде |
/ |
|
дұрыс |
кескіндейді, әрі |
|||||
|
кескіндейді |
және |
кескіндеп, |
|
|
нүктелердің |
|
|
|
оның |
координаталарын |
|||
|
нүктелердің |
|
координаталарын |
координаталарын |
дұрыс анықтайды. |
|||||||||
|
координаталарын |
табуда қиналады. |
табуда |
қателіктер |
|
|
|
|
|
|||||
|
табады. |
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
екі |
Кеңістіктегі |
|
екі |
Кеңістіктегі |
екі |
|||||
|
Кеңістіктегі |
екі |
нүктенің |
|
|
нүктенің |
|
|
|
нүктенің |
|
|
|
|
|
арақашықтығын |
|
|
арақашықтығын табу |
арақашықтығын дұрыс |
|||||||||
|
нүктенің |
|
табуда қиналады. |
формуласын |
|
|
|
табады. |
|
|
|
|||
|
арақашықтығын |
|
|
|
қолданады, |
есептеуде |
|
|
|
|
|
|||
|
табады. |
|
|
|
|
қателіктер жібереді. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сфераның теңдеуін |
Сфераның |
теңдеуін |
Сфераның |
теңдеуін |
|||||||
|
|
|
қолдануда |
|
|
қолданады, |
|
|
|
дұрыс |
|
қолданады, |
||
|
Сфераның |
теңдеуін |
қиналады. |
|
|
түрлендіруді |
тапсырманы |
дұрыс |
||||||
|
түрлендіреді. |
|
|
|
|
орындауда |
қателіктер |
толығымен |
||||||
|
|
|
|
|
жібереді. |
|
|
|
орындайды. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17
4-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» тарауы бойынша
жиынтық бағалау
|
Бөлімше |
Кеңістіктегі вектордың координаталары |
|
|
|||
|
|
Векторлардың коллинеарлығы және компланарлығы |
|||||
|
|
Векторларды қосу,векторды санға көбейту |
|
|
|||
|
|
Векторлардың скаляр көбейтіндісі |
|
|
|
||
|
Оқу мақсаты |
10.4.5 |
Кеңістіктегі вектордың координаталарын |
және |
|||
|
|
|
ұзындығын таба білу |
|
|
|
|
|
|
10.4.6 |
Кеңістіктегі |
коллинеар |
және |
компланар |
|
|
|
|
векторлардың |
анықтамаларын, |
векторлардың |
||
|
|
|
коллинеарлық шартын білу |
|
|
||
|
|
10.4.7 |
Векторларды қосу және азайтуды, векторды санға |
||||
|
|
|
көбейтуді орындау |
|
|
|
|
|
|
10.4.8 |
Координаталық |
түрдегі |
векторлардың |
скаляр |
|
|
|
|
көбейтіндісі формуласын білу және оны есептер |
||||
|
|
|
шығаруда қолдану |
|
|
|
|
|
Бағалау критерийі |
Білім алушы |
|
|
|
|
|
-
Кеңістіктегі вектордың ұзындығы формуласын қолданады
-
Векторлардың коллинеарлық шартын қолданады
-
Векторларды қосу және азайтуды, векторды санға көбейтуді орындайды
-
Векторлардың скаляр көбейтіндісі формуласын қолданады
Ойлау дағдыларының Қолдану
деңгейлері
Орындау уақыты 20 минут
Тапсырма
![]()
-
Егер A(0;1; 2), B(5; 2; 2 ) болса, онда -ның қандай мәнінде AB векторының ұзындығы
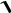
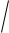 30
болады?
30
болады?
![]()
|
2. |
|
|
|
(0;6; 2) векторларының коллинеар болатынын дәлелдеңіз |
|
a (0;3;1) |
және b |
|||
|
3. |
a 0; 4; 7 |
және b 7; 9; 1 векторлары берілген. 3a 2b және a 4b |
||
|
табыңыз. |
|
|
|
|
![]()
![]()
![]()
![]()
![]()
![]()
-
⃗⃗⃗⃗⃗ = (1; 3; −1) және ⃗⃗⃗⃗⃗ = (4; 2; ) векторлары берілген. Егер = 900 екені белгілі болса, онда − ның мәнін табыңыз.
18
|
Бағалау критерийі |
Тапсырма |
|
Дескриптор |
|
|
Балл |
|||
|
№ |
Білім алушы |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
Кеңістіктегі вектордың |
|
вектор координаталарын өрнектейді |
1 |
||||||
|
ұзындығы формуласын |
|
вектор ұзындығын |
табу |
формуласын |
1 |
||||
|
қолданады |
|
|
|
қолданады |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
-ға қатысты теңдеу құрады |
|
|
1 |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
теңдеуді шешу тәсілін таңдайды |
|
1 |
|||
|
|
|
|
|
белгісіз айнымалының мәнін табады |
1 |
||||
|
|
|
|
|
|
|
|
|||
|
Векторлардың |
|
|
векторлардың |
коллинеарлық |
шартын |
1 |
|||
|
коллинеарлық |
шартын |
|
қолданады |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
қолданады |
|
|
2 |
вектордың нөлдік |
емес |
компонентін |
1 |
||
|
|
|
|
табады |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторлардың |
коллинеарлығы |
туралы |
1 |
||
|
|
|
|
|
қорытынды жасайды |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Векторларды |
|
қосу |
|
векторды санға көбейтуді орындайды |
1 |
||||
|
және |
азайтуды, |
|
|||||||
|
3 |
|
|
|
|
|
|
|||
|
векторларды азайтуды орындайды |
1 |
||||||||
|
векторды |
|
санға |
|||||||
|
көбейтуді орындайды |
|
|
|
|
|
|
|
||
|
|
векторларды қосуды орындайды |
|
1 |
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
Векторлардың |
скаляр |
|
векторлардың |
скаляр көбейтіндісінің |
1 |
||||
|
көбейтіндісі |
|
|
|
формуласын қолданады |
|
|
|||
|
|
|
|
|
|
|
||||
|
формуласын |
|
|
4 |
векторлардың перпендикулярлық шартын |
1 |
||||
|
қолданады |
|
|
қолданады |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
белгісіз айнымалының мәнін табады |
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Барлығы: |
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
19
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ___________________________________________
|
Бағалау критерийі |
|
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|||||||||
|
|
|
|
|
Төмен |
|
|
|
Орта |
|
|
|
Жоғары |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Кеңістіктегі |
вектор |
Кеңістіктегі |
|
|
|
Кеңістіктегі вектордың |
Кеңістіктегі вектордың |
|||||||||
|
ұзындығының |
|
вектордың |
|
|
|
координаталарын |
/ |
|
координаталарын және |
|||||||
|
формуласын |
|
координаталарын |
ұзындығын |
|
табуда |
ұзындығын |
дұрыс |
|||||||||
|
қолданады |
|
және |
ұзындығын |
қателіктер жібереді. |
|
|
табады. |
|
|
|
||||||
|
|
|
|
табуда қиналады. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторлардың |
|
Кеңістіктегі |
|
|
|
Кеңістіктегі коллинеар |
Кеңістіктегі |
|
|
|
||||||
|
коллинеарлық шартын |
векторлардың |
|
|
|
векторлардың |
|
|
|
векторлардың |
|
|
|
||||
|
қолданады |
|
коллинеарлық |
|
|
|
коллинеарлық шартын |
коллинеарлық шартын |
|||||||||
|
|
|
|
шартын қолдануда |
қолдануда |
қателіктер |
дұрыс қолданады. |
||||||||||
|
|
|
|
қиналады. |
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторларды |
қосу |
Векторларды |
қосу |
Векторларды |
қосу |
/ |
|
Векторларды қосу және |
||||||||
|
және |
азайтуды, |
және |
азайтуды, |
азайтуды / |
векторды |
азайтуды, |
векторды |
|||||||||
|
векторды |
|
санға |
векторды |
санға |
санға |
көбейтуді |
санға көбейтуді дұрыс |
|||||||||
|
көбейтуді |
|
көбейтуді |
|
|
|
орындауда |
қателіктер |
орындайды. |
|
|
|
|||||
|
орындайды |
|
орындауда |
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
||
|
|
|
|
қиналады. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторлардың |
|
Векторлардың |
|
|
|
Векторлардың |
скаляр |
Векторлардың |
скаляр |
|||||||
|
скаляр |
көбейтіндісі |
скаляр |
көбейтіндісі |
көбейтіндісі |
|
|
|
|
көбейтіндісі |
|
|
|
||||
|
формуласын |
|
формуласын |
|
|
|
формуласын |
|
|
|
формуласын |
есептер |
|||||
|
қолданады |
|
қолдануда |
|
|
|
қолданады, |
есептеулер |
шығаруда |
дұрыс |
|||||||
|
|
|
|
қиналады. |
|
|
|
жүргізуде |
қателіктер |
қолданады. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
10-сынып ҚГБ БЖБ
10-сынып ҚГБ БЖБ
«Геометрия» пәнінен
Жиынтық бағалауға арналғанәдістемелік ұсыныстар
10-сынып
(қоғамдық-гуманитарлық бағыты)
Нұр-Сұлтан – 2019
Әдістемелік ұсыныстар мұғалімге 10-сынып білім алушыларына «Геометрия» пәні бойынша жиынтық бағалауды жоспарлау, ұйымдастыру және өткізуге көмек құралы ретінде құрастырылған. Бөлім бойынша жиынтық бағалаудың тапсырмалары мұғалімге білім алушылардың тоқсан бойынша жоспарланған оқу мақсаттарына жету деңгейін анықтауға мүмкіндік береді.
Әдістемелік ұсыныста бөлім бойынша жиынтық бағалауды өткізуге арналған бағалау критерийі мен дескрипторлары бар тапсырмалар ұсынылған. Сондай-ақ жинақта білім алушылардың оқу жетістіктерінің мүмкін деңгейлері (рубрикалар) сипатталған. Дескрипторлары мен балдары бар тапсырмалар ұсыныс түрінде берілген.
Әдістемелік ұсыныс мұғалімдерге, мектеп әкімшілігіне, білім беру бөлімінің әдіскерлеріне, критериалды бағалау бойынша мектеп, өңірлік үйлестірушілеріне және басқа да мүдделі тұлғаларға арналған.
Әдістемелік ұсынысты дайындау барысында ресми интернет-сайттағы қолжетімді ресурстар (суреттер, фотосуреттер, мәтіндер, аудио және бейнематериалдар) қолданылды.
2
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 4
«Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы»
бөлімі бойынша жиынтық бағалау 4
2-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 8
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау 8
3-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 12
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау 12
4-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР 18
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» тарауы бойынша
3
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы»
бөлімі бойынша жиынтық бағалау
Тақырып Стереометрия аксиомалары және олардың салдарлары
Кеңістіктегі екі түзудің өзара орналасуы
Түзу мен жазықтықтың өзара орналасуы
Екі жазықтықтың өзара орналасуы
Оқу мақсаты 10.2.1 Стереометрия аксиомаларын, олардың салдарларын
білу және оларды математикалық символдар арқылы
жазып көрсету
10.2.2 Кеңістіктегі параллель және айқас түзулердің
анықтамаларын білу және оларды анықтау және
кескіндеу
10.2.3 Кеңістіктегі параллель түзулердің қасиеттерін білу
және оларды есептер шығаруда қолдану
10.2.4 Түзу мен жазықтықтың параллельдік және
перпендикулярлық белгілерін, қасиеттерін білу және
оларды есептер шығаруда қолдану
10.2.5 Жазықтықтардың параллельдігі мен
перпендикулярлығының белгілерін білу және
оларды есептер шығаруда қолдану
Бағалау критерийі Білім алушы
Стеореметрия аксиомаларын және олардың салдарын
қолданады
Кеңістіктегі түзулердің өзара орналасуын анықтайды
Түзу мен жазықтықтың параллельдік белгісін
қолданады
Жазықтықтардың параллельдік қасиетін қолданады
Ойлау дағдыларының Қолдану
деңгейі
Орындау уақыты 25 минут
Тапсырма
-
Берілген символдық жазу бойынша сызбаны салып, дәлелдеңіз:
( ∩ )= , ∈ , ∉ ⇨ ⊄
-
Төменде АВСDA1B1C1D1 текшесінің суреті берілген. Келесі түзулер жұбының орналасуын анықтаңыз:
-
QP және AD1, мұндағы Q және Р сәйкесінше DD1 және AD кесінділерінің орталары;
-
-
AD1 және A1P;
-
MN және AD1, мұндағы M және N сәйкесінше A1B1 және BB1 кесінділеріне тиісті;
-
CD және A1 P;
-
MN және AB?
Қиылысатын түзулер үшін қиылысу нүктесін анықтаңыз, ал айқас және параллель түзулер үшін сәйкес белгіні қолданып жазыңыз.
4
-
АВ кесіндісі 15 см-ге тең және α жазықтығында жатыр. С нүктесі α жазықтығына тиісті емес. К және М нүктелері сәйкесінше АС мен ВС кесінділерінің орталары.
а) КМ түзуінің α жазықтығымен ортақ нүктелері болуы мүмкін бе? Жауабыңызды негіздеңіз.
-
К және М нүктелерінің арақашықтығы неге тең?

-
a және b түзулері О нүктесінде қиылысады. Олар және параллель жазықтықтарын суретте көрсетілгендей, А, А1, В, В1 нүктелерінде қияды. АВ және ОВ1 ұзындықтарын табыңыз.

5
|
Бағалау критерийі |
Тапсырма |
|
|
Дескриптор |
|
Балл |
||
|
№ |
Білім алушы |
|
||||||
|
|
|
|
|
|
||||
|
Стеореметрия |
|
|
қиылысушы жазықтықтарды салады; |
1 |
||||
|
аксиомаларын |
және |
1 |
сызбада PQ-дің β-ны қиғаны көрінеді; |
1 |
||||
|
олардың |
|
салдарын |
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
аксиомаларды/салдарларды |
қолданып |
|
|||||
|
қолданады |
|
|
|
1 |
||||
|
|
|
|
тұжырым жасайды; |
|
||||
|
|
|
|
|
|
|
|||
|
Кеңістіктегі түзулердің |
|
параллель түзулерді анықтайды; |
1 |
|||||
|
өзара |
орналасуын |
|
параллель түзулердің белгісін жазады; |
1 |
||||
|
анықтайды |
|
|
|
қиылысатын түзулерді табады; |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
қиылысатын |
түзулердің |
қиылысу |
1 |
|
|
|
|
|
|
нүктелерін табады; |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
айқас түзулерді табады; |
|
1 |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
айқас түзулердің белгісін жазады; |
1 |
|||
|
|
|
|
|
|||||
|
Түзу мен жазықтықтың |
|
түзулердің параллельділігін анықтайды; |
1 |
|||||
|
параллельдік |
белгісін |
3 |
түзу |
мен |
жазықтықтың параллельдік |
1 |
||
|
қолданады |
|
|
белгісін қолданады; |
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
ұзындықты анықтайды; |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Жазықтықтардың |
|
параллель |
жазықтықтардың |
қасиетін |
1 |
|||
|
параллельдік |
қасиетін |
|
қолданады; |
|
|
|||
|
|
|
|
|
|||||
|
қолданады |
|
|
4 |
үшбұрыштардың ұқсастығын |
анықтап, |
|
||
|
|
|
|
сәйкес |
қабырғалардың |
қатынасын |
1 |
||
|
|
|
|
|
|||||
|
|
|
|
|
жазады; |
|
|
|
|
|
|
|
|
|
белгісізді табады. |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
Барлығы: |
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
6
Стереометрия аксиомалары. Кеңістіктегі түзулер мен жазықтықтар өзара орналасуы» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ______________________________________________________
|
|
Бағалау критерийі |
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|||||
|
|
|
|
|
Төмен |
Орта |
|
|
|
Жоғары |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
Стеореметрия |
аксиомаларын |
Стереометрия |
аксиомаларын, |
Стереометрия |
|
|
Стереометрия |
аксиомаларын, |
|||||
|
және |
олардың |
салдарын |
олардың |
|
салдарларын |
аксиомаларын, |
олардың |
|
олардың |
|
салдарларын, |
||
|
қолданады |
|
қолдануда қиналады. |
салдарларын |
|
қолдануда |
|
математикалық символикасын |
||||||
|
|
|
|
|
|
|
қателіктер жібереді. |
|
дұрыс қолданады. |
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
Кеңістіктегі түзулердің өзара |
Кеңістіктегі |
түзулердің өзара |
Кеңістіктегі |
|
параллель/ |
|
Кеңістіктегі түзулердің өзара |
||||||
|
орналасуын анықтайды |
орналасуын |
анықтауда |
айқас/ қиылысатын түзулерді |
|
орналасуын |
|
дұрыс |
||||||
|
|
|
|
қиналады. |
|
анықтауда |
|
қателіктер |
|
анықтайды. |
|
|
||
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Түзу |
мен |
жазықтықтың |
Түзу |
мен |
жазықтықтың |
Түзумен |
жазықтықтың |
|
Түзу |
мен |
жазықтықтың |
||
|
параллельдік |
белгісін |
параллельдік |
белгісін |
параллельдік |
|
белгісін |
|
параллельдік |
белгісін |
дұрыс |
|||
|
қолданады |
|
қолдануда қиналады. |
қолданады, |
бірақ |
жауапты |
|
қолданады. |
|
|
||||
|
|
|
|
|
|
|
негіздеуде |
|
қателіктер |
|
|
|
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Жазықтықтардың |
параллельдік |
Жазықтықтардың параллельдік |
Жазықтықтардың |
|
|
Жазықтықтардың |
|
||||||
|
қасиетін қолданады |
қасиетін қолдануда қиналады. |
параллельдік |
|
қасиетін |
|
параллельдік |
қасиетін |
||||||
|
|
|
|
|
|
|
қолданады, |
|
бірақ |
|
қолданып, |
есепті |
дұрыс |
|
|
|
|
|
|
|
|
есептеулерде |
|
қателіктер |
|
шығарады. |
|
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау
Тақырып
Кеңістіктегі түзулер арасындағы бұрыш
Перпендикуляр және көлбеу
Үш перпендикуляр туралы теорема
Оқу мақсаты
10.2.6 Кеңістіктегі екі түзу арасындағы бұрыш
анықтамасын білу
10.3.5 Кеңістіктегі перпендикуляр, көлбеу және
көлбеудің проекциясы анықтамаларын білу
10.3.1 Үш перпендикуляр туралы теореманы білу және
оны есептер шығаруда қолдану
Бағалау критерийі
Білім алушы
Кеңістіктегі екі түзу арасындағы бұрышты
табады
Ойлау дағдыларының
деңгейлері
Орындау уақыты
Кеңістіктегі перпендикуляр, көлбеу және
көлбеудің проекциясы анықтамаларын қолданады
Үш перпендикуляр туралы теореманы
қолданады
Қолдану
25 минут
Тапсырма
-
ABCDA1B1C1D1 - текше. A1B1 және C1D1 қырларында сәйкесінше N және M
нүктелері берілген, MDC NBA 600 . NB және MD кесінділері арасындағы бұрышты табыңыз.

-
M нүктесінен жазықтығына MA, MB көлбеулері және MO перпендикуляры жүргізілген.
-
көлбеулердің жазықтығына проекциясын салыңыз;
b) егер = 600, = 450, = 16 см болса, проекциялардың ұзындығын табыңыз.
-
a түзуі ABC жазықтығына перпендикуляр, MD 13 см, АС=15см, ВС=20см. АВС үшбұрышы тікбұрышты: = 900.
MC кесіндісінің ұзындығын табыңыз.

9
|
Бағалау критерийі |
Тапсырма |
|
Дескриптор |
|
Балл |
||
|
№ |
|
Білім алушы |
|
||||
|
|
|
|
|
|
|
||
|
Кеңістіктегі |
екі түзу |
|
NB немесе MD түзуін екінші түзумен |
1 |
|||
|
арасындағы |
бұрышты |
1 |
қиылысқанша параллель көшіреді; |
|
|||
|
табады |
|
|
|
|
|
|
|
|
|
|
NB және MD кесінділері арасындағы |
1 |
||||
|
|
|
|
|||||
|
|
|
|
|
бұрышты анықтайды; |
|
|
|
|
Кеңістіктегі |
|
2a |
көлбеулердің проекцияларын салады |
1 |
|||
|
перпендикуляр, көлбеу |
|
бұрыштың |
тангенсінің |
анықтамасын |
1 |
||
|
және |
|
көлбеудің |
|
қолданады; |
|
||
|
|
|
|
|
||||
|
проекциясы |
|
2b |
теңбүйірлі |
тікбұрышты |
үшбұрыштың |
1 |
|
|
анықтамаларын |
|
қасиетін қолданады; |
|
||||
|
|
|
|
|||||
|
қолданады |
|
|
проекциялардың ұзындықтарын табады; |
1 |
|||
|
|
|
|
|
|
|
|
|
|
Үш |
перпендикуляр |
|
∆ABC |
тікбұрышты |
үшбұрышына |
1 |
|
|
туралы |
|
теореманы |
|
Пифагор теоремасын қолданады; |
|||
|
|
|
|
|||||
|
қолданады |
|
|
гипотенуза ұзындығын есептейді; |
1 |
|||
|
|
|
|
|
|
|
||
|
|
|
|
3 |
үш перпендикуляр туралы теореманы |
1 |
||
|
|
|
|
қолданады; |
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
үшбұрыштың тік бұрышынан түсірілген |
1 |
||
|
|
|
|
|
биіктіктің ұзындығын табады; |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
ізделінді кесінді ұзындығын табады; |
1 |
||
|
|
|
|
|
|
|
|
|
|
Барлығы: |
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
10
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ___________________________________________
|
Бағалау критерийі |
|
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|
|||||||||
|
|
|
|
Төмен |
|
|
|
Орта |
|
|
|
|
|
Жоғары |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Кеңістіктегі екі |
түзу |
Кеңістіктегі |
|
екі |
Кеңістіктегі екі |
түзу |
Кеңістіктегі |
екітүзу |
||||||||||
|
арасындағы |
|
түзу |
арасындағы |
арасындағы |
|
|
|
|
арасындағы |
|
бұрышты |
|||||||
|
бұрышты табады |
бұрышты |
табуда |
бұрышты |
табуда |
дұрыс табады. |
|
|
|
|
|||||||||
|
|
|
|
қиналады. |
|
|
|
қателіктер жібереді. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
|
Кеңістіктегі |
|
|
|
Кеңістіктегі |
|
|
|
|
Кеңістіктегі |
|
|
|
|
|||
|
перпендикуляр, |
|
перпендикуляр, |
перпендикуляр |
/ |
|
перпендикуляр, |
көлбеу |
|||||||||||
|
көлбеу |
|
және |
көлбеу |
|
және |
көлбеу |
|
|
|
|
және |
|
көлбеудің |
|||||
|
көлбеудің |
|
|
көлбеудің |
|
|
|
анықтамаларын |
|
|
|
проекциясы |
|
|
|
|
|||
|
проекциясы |
|
проекциясы |
|
|
|
қолданады, |
|
бірақ |
анықтамаларын |
дұрыс |
||||||||
|
анықтамаларын |
|
анықтамаларын |
көлбеудің |
|
|
|
|
қолданады. |
|
|
|
|
||||||
|
қолданады |
|
|
қолдануда |
|
|
|
проекциясын |
табуда |
|
|
|
|
|
|
||||
|
|
|
|
қиналады. |
|
|
|
қателіктер жібереді. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Үш перпендикуляр |
Үш перпендикуляр |
Үш перпендикуляр |
Үш |
перпендикуляр |
||||||||||||||
|
туралы |
теореманы |
туралы |
теореманы |
туралытеореманы |
туралы теореманы дұрыс |
|||||||||||||
|
қолданады |
|
|
қолдануда |
|
|
|
қолданады, |
|
|
|
|
қолданып, |
|
есептің |
||||
|
|
|
|
қиналады. |
|
|
|
есептеулер |
|
|
|
|
шешімін дұрыс табады. |
||||||
|
|
|
|
|
|
|
|
|
жүргізуде қателіктер |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
3-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалау
|
Тақырып |
|
Түзу мен жазықтық арасындағы бұрыш |
|
|||
|
|
|
Екі жазықтық арасындағы бұрыш. Екіжақты бұрыш |
||||
|
|
|
Кеңістіктегі арақашықтық |
|
|
||
|
Оқу мақсаты |
10.3.2 Түзу мен |
жазықтық |
арасындағы |
бұрыштың |
||
|
|
|
|
анықтамасын білу, кескіндей алу және оның |
|||
|
|
|
|
шамасын табу |
|
|
|
|
|
|
10.3.3 Жазықтықтар |
арасындағы бұрыштың |
(екіжақты |
||
|
|
|
|
бұрыш) анықтамасын білу, кескіндей алу және |
|||
|
|
|
|
оның шамасын табу |
|
|
|
|
|
|
10.3.4 Нүктеден жазықтыққа дейінгі және айқас түзулер |
||||
|
|
|
|
арасындағы арақашықтықтарды таба білу |
|||
|
Бағалау критерийі |
Білім алушы |
|
|
|
||
|
|
|
|
Түзу мен жазықтық арасындағы бұрыштың |
|||
|
|
|
шамасын табады |
|
|
|
|
|
|
|
|
Жазықтықтар арасындағы бұрыштың (екіжақты |
|||
|
|
|
бұрыш) шамасын табады |
|
|
||
|
|
|
|
Нүктеден жазықтыққа |
дейінгі арақашықтықты |
||
|
|
|
табады |
|
|
|
|
|
Ойлау |
дағдыларының |
Қолдану |
|
|
|
|
|
деңгейлері |
|
|
|
|
|
|
|
Орындау уақыты |
25 минут |
|
|
|
||
Тапсырма
-
ABCDA' B'C' D' бірлік текшесі (куб).
а) ABC жазықтығы мен AC' түзуі арасындағы бұрыштың косинусын табыңыз;
-
егер M нүктесі AB қырының ортасы болса, онда MA’D және CA’D жазықтықтарының арасындағы бұрыштың косинусын табыңыз.
-
А нүктесінен жазықтығына ұзындығы 17 см болатын көлбеу жүргізілген. Осы көлбеудің жазықтығындағы проекциясы 15 см-ге тең.
Есептің шарты бойынша сызбаны салыңыз және А нүктесінен жазықтығына дейінгі қашықтықты табыңыз.
12
|
Бағалау критерийі |
Тапсырма |
|
|
Дескриптор |
|
Балл |
|||
|
№ |
Білім алушы |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
түзу мен жазықтық арасындағы бұрышты |
1 |
|||||
|
|
|
|
кескіндейді; |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
Түзу мен жазықтықтың |
|
кубтың диагоналін есептейді; |
|
1 |
|||||
|
арасындағы бұрыштың |
1а |
тікбұрышты |
үшбұрыштағы қатынасты |
1 |
|||||
|
шамасын табады. |
|
қолданады; |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
түзу |
мен |
жазықтық |
арасындағы |
1 |
||
|
|
|
|
бұрыштың косинусын табады; |
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
сызбаны салады; |
|
|
|
1 |
||
|
|
|
|
МA1D және CA1D жазықтықтары A1D |
1 |
|||||
|
|
|
|
түзуі |
бойымен |
қиылысатынын |
||||
|
|
|
|
анықтайды; |
|
|
|
|
|
|
|
Жазықтықтар |
|
MA1D |
теңбүйірліүшбұрышының |
|
|||||
|
|
медианасы |
A1D -ға |
перпендикуляр |
1 |
|||||
|
арасындағы бұрыштың |
1b |
болатынын көрсетеді; |
|
|
|
||||
|
(екіжақты |
бұрыш) |
|
|
|
|||||
|
|
MA1D |
және |
|
CA1D |
жазықтықтары |
|
|||
|
шамасын табады |
|
|
|
||||||
|
|
арасындағы |
|
екіжақты |
бұрышты |
1 |
||||
|
|
|
|
|
||||||
|
|
|
|
анықтайды; |
|
|
|
|
|
|
|
|
|
|
тікбұрышты үшбұрыштағы сүйір бұрыш |
1 |
|||||
|
|
|
|
тангенсінің анықтамасын қолданады; |
||||||
|
|
|
|
|
||||||
|
|
|
|
жазықтықтардың |
арасындағы |
бұрышты |
1 |
|||
|
|
|
|
табады; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Нүктеден |
жазықтыққа |
|
сызбаны салады; |
|
|
|
1 |
||
|
дейінгі |
|
|
|
|
|
|
|
|
|
|
|
|
Анүктесінен |
жазықтыққа |
дейінгі |
1 |
||||
|
арақашықтықты |
2 |
||||||||
|
қашықтықты сызбада көрсетеді; |
|
||||||||
|
|
|
||||||||
|
табады |
|
|
|
|
|
|
|
|
|
|
|
|
нүктеден |
жазықтыққа |
дейінгі |
1 |
||||
|
|
|
|
|||||||
|
|
|
|
қашықтықты анықтайды; |
|
|
||||
|
|
|
|
|
|
|
||||
|
Барлығы: |
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
13
«Кеңістіктегі бұрыш. Кеңістіктегі арақашықтық» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ___________________________________________
|
Бағалау критерийі |
|
Оқу жетістіктерінің деңгейлері |
|
|
||||
|
|
|
Төмен |
Орта |
|
Жоғары |
|||
|
|
|
|
|
|
|
|
|
|
|
Түзу мен жазықтық |
Түзу мен жазықтық |
Түзу мен |
жазықтық |
Түзу |
мен |
жазықтық |
||
|
арасындағы |
|
арасындағы |
арасындағы |
бұрыштың |
||||
|
арасындағы |
|
|
||||||
|
|
бұрыштың |
|
бұрыштың |
шамасын |
шамасын дұрыс табады. |
|||
|
бұрыштың |
шамасын |
|
||||||
|
шамасын |
табуда |
табуда |
қателіктер |
|
|
|
||
|
табады. |
|
|
|
|
||||
|
|
қиналады. |
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
Жазықтықтар |
Жазықтықтар |
Жазықтықтар |
Жазықтықтар |
|
||||
|
арасындағы |
|
арасындағы |
|
арасындағы |
арасындағы |
бұрыштың |
||
|
бұрыштың (екіжақты |
бұрыштың |
|
бұрышты |
(екіжақты |
(екіжақты |
бұрыш) |
||
|
бұрыш) |
шамасын |
(екіжақты |
бұрыш) |
бұрыш) анықтайды, |
шамасын дұрыс табады. |
|||
|
табады. |
|
шамасын |
табуда |
бұрыштың |
шамасын |
|
|
|
|
|
|
қиналады. |
|
табуда |
қателіктер |
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нүктеден |
|
Нүктеден |
|
Нүктеден |
|
Нүктеден |
жазықтыққа |
|
|
жазықтыққа |
дейінгі |
жазықтыққа дейінгі |
жазықтыққа дейінгі |
дейінгі |
арақашықтықты |
|||
|
арақашықтықты |
арақашықтықты |
арақашықтықты |
дұрыс табады. |
|||||
|
табады. |
|
табуда қиналады. |
табуда |
қателіктер |
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
14
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» бөлімі бойынша жиынтық бағалау
|
Тақырып |
|
|
|
|
|
Кеңістіктегі тікбұрышты координаталар жүйесі |
|||||||||||||
|
|
|
|
|
|
|
|
Екі нүктенің арақашықтығы |
|
|
||||||||||
|
|
|
|
|
|
|
|
Кесінді ортасының координаталары |
|
|||||||||||
|
|
|
|
|
|
|
|
Сфера теңдеуі |
|
|
|
|||||||||
|
Оқу мақсаты |
|
|
|
|
|
10.4.1 Кеңістіктегі |
тікбұрышты |
координаталар жүйесін |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
жазықтықта кескіндей алу және оны сипаттау |
|||||||
|
|
|
|
|
|
|
|
10.4.2 Кеңістіктегі екі нүкте арасындағы арақашықтықты |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
таба білу |
|
|
|
||||
|
|
|
|
|
|
|
|
10.4.3 Кеңістіктегі |
кесінді ортасының |
координаталарын |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
таба білу |
|
|
|
||||
|
|
|
|
|
|
|
|
10.4.4 Сфера теңдеуін білу және оны есептер шығаруда |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
қолдану |
|
|
|
||||
|
Бағалау критерийі |
|
|
|
|
Білім алушы |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
тікбұрышты |
координаталар |
||||
|
|
|
|
|
|
|
|
|
|
|
жүйесінде нүктелерді кескіндейді және нүктелердің |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
координаталарын табады. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
екі |
нүкте |
арасындағы |
|||
|
|
|
|
|
|
|
|
|
|
|
арақашықтықты табады |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сфера теңдеуін түрлендіреді |
|
|||||
|
Ойлау |
дағдыларының |
Қолдану |
|
|
|
||||||||||||||
|
деңгейлері |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Орындау уақыты |
|
|
|
|
|
25 минут |
|
|
|
||||||||||
|
Тапсырма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1. a) |
Кеңістікте |
C |
3; |
|
; |
5 |
|
3 нүктесі берілген. С нүктесінің Oxy; Oxz; Oyz |
|||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
![]()
![]()
![]()
![]()
жазықтықтарындағы және Ox; Oy; Oz осьтеріндегі проекциясының координаталарын табыңыз.
-
Тікбұрышты координаталар жүйесінде келесі нүктелерді салыңыз:
A(1;2;3), B(2;0;1), C(0;0;3), D(3; 2;0)
-
ABC үшбұрышы берілген, мұндағы A(1; 3; 2), B(0; 2; 4), C(1; 1; 4).
Егер А1 нүктесі ВС қабырғасының ортасы болса, онда АА1 кесіндісінің ұзындығын табыңыз.
3. Сфера x2 y2 z 2 4x 8z 5 теңдеуімен берілген. A1; m; 4 нүктеcі сфераның
бойында орналасқан.
a) сфера центрінің координаталары мен оның радиусын табыңыз.
b) m – нің мәнін табыңыз.
15
|
Бағалау критерийі |
Тапсырма |
|
Дескриптор |
|
|
Балл |
||||
|
№ |
Білім алушы |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
Кеңістіктегі |
|
|
Oxy жазықтығына тиісті нүктені табады; |
1 |
||||||
|
|
|
Oxz және Oyz |
жазықтықтарына |
тиісті |
1 |
|||||
|
тікбұрышты |
|
|
||||||||
|
|
1a |
нүктелерді табады; |
|
|
|
|
||||
|
координаталар |
|
|
|
|
|
|||||
|
|
Ox; Oy; |
Oz осьтеріне тиісті |
нүктелерді |
|
||||||
|
жүйесінде |
нүктелерді |
|
1 |
|||||||
|
|
табады ; |
|
|
|
|
|
|
|||
|
кескіндейді |
және |
|
|
|
|
|
|
|
|
|
|
|
тікбұрышты |
координаталар |
жүйесін |
|
||||||
|
нүктелердің |
|
|
1 |
|||||||
|
|
|
салады; |
|
|
|
|
|
|
||
|
координаталарын |
1b |
|
|
|
|
|
|
|
||
|
берілген |
нүктелерді |
координаталар |
|
|||||||
|
табады. |
|
|
1 |
|||||||
|
|
|
жүйесінде салады. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
Кеңістіктегі |
кесінді |
|
ВС |
кесіндісінің |
|
ортасының |
1 |
|||
|
|
координаттарын анықтайды; |
|
|
|||||||
|
|
|
|
|
|||||||
|
ортасының |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Кесіндісінің |
ұзындығын |
анықтау |
1 |
|||||
|
координаталарын |
||||||||||
|
|
формуласын қолданады; |
|
|
|
||||||
|
табады. |
|
|
|
|
|
|
||||
|
|
|
АА1 кесіндісінің ұзындығын анықтайды; |
1 |
|||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
толық |
квадратты |
бөліп |
алу |
тәсілін |
1 |
||
|
|
|
|
қолданады; |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
Сфераның |
теңдеуін |
3a |
түрлендірулерді орындайды; |
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
||
|
түрлендіреді. |
|
шеңбер |
центрінің |
координаталары мен |
1 |
|||||
|
|
|
|
радиусын табады; |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
3b |
А нүктесіне сәйкес теңдеуді шешеді; |
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
белгісіз айнымалының мәнін табады; |
1 |
|||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Барлығы: |
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
16
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ___________________________________________
|
Бағалау критерийі |
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|
|||||||
|
|
|
Төмен |
|
|
Орта |
|
Жоғары |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
|
|
Кеңістіктегі |
|
|
|
Кеңістіктегі |
|
|
|
|
|
Кеңістіктегі |
|
тікбұрышты |
|
|
тікбұрышты |
|
|
|
тікбұрышты |
|
|
|
|
|
тікбұрышты |
|
координаталар |
|
|
координаталар |
координаталар |
|||||||
|
координаталар |
жүйесінде |
|
|
жүйесінде |
нүктелерді |
жүйесінде |
нүктелерді |
||||||
|
жүйесінде нүктелерді |
нүктелерді |
|
|
кескіндеуде |
/ |
|
дұрыс |
кескіндейді, әрі |
|||||
|
кескіндейді |
және |
кескіндеп, |
|
|
нүктелердің |
|
|
|
оның |
координаталарын |
|||
|
нүктелердің |
|
координаталарын |
координаталарын |
дұрыс анықтайды. |
|||||||||
|
координаталарын |
табуда қиналады. |
табуда |
қателіктер |
|
|
|
|
|
|||||
|
табады. |
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кеңістіктегі |
екі |
Кеңістіктегі |
|
екі |
Кеңістіктегі |
екі |
|||||
|
Кеңістіктегі |
екі |
нүктенің |
|
|
нүктенің |
|
|
|
нүктенің |
|
|
|
|
|
арақашықтығын |
|
|
арақашықтығын табу |
арақашықтығын дұрыс |
|||||||||
|
нүктенің |
|
табуда қиналады. |
формуласын |
|
|
|
табады. |
|
|
|
|||
|
арақашықтығын |
|
|
|
қолданады, |
есептеуде |
|
|
|
|
|
|||
|
табады. |
|
|
|
|
қателіктер жібереді. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сфераның теңдеуін |
Сфераның |
теңдеуін |
Сфераның |
теңдеуін |
|||||||
|
|
|
қолдануда |
|
|
қолданады, |
|
|
|
дұрыс |
|
қолданады, |
||
|
Сфераның |
теңдеуін |
қиналады. |
|
|
түрлендіруді |
тапсырманы |
дұрыс |
||||||
|
түрлендіреді. |
|
|
|
|
орындауда |
қателіктер |
толығымен |
||||||
|
|
|
|
|
жібереді. |
|
|
|
орындайды. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17
4-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУҒА АРНАЛҒАН ТАПСЫРМАЛАР
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» тарауы бойынша
жиынтық бағалау
|
Бөлімше |
Кеңістіктегі вектордың координаталары |
|
|
|||
|
|
Векторлардың коллинеарлығы және компланарлығы |
|||||
|
|
Векторларды қосу,векторды санға көбейту |
|
|
|||
|
|
Векторлардың скаляр көбейтіндісі |
|
|
|
||
|
Оқу мақсаты |
10.4.5 |
Кеңістіктегі вектордың координаталарын |
және |
|||
|
|
|
ұзындығын таба білу |
|
|
|
|
|
|
10.4.6 |
Кеңістіктегі |
коллинеар |
және |
компланар |
|
|
|
|
векторлардың |
анықтамаларын, |
векторлардың |
||
|
|
|
коллинеарлық шартын білу |
|
|
||
|
|
10.4.7 |
Векторларды қосу және азайтуды, векторды санға |
||||
|
|
|
көбейтуді орындау |
|
|
|
|
|
|
10.4.8 |
Координаталық |
түрдегі |
векторлардың |
скаляр |
|
|
|
|
көбейтіндісі формуласын білу және оны есептер |
||||
|
|
|
шығаруда қолдану |
|
|
|
|
|
Бағалау критерийі |
Білім алушы |
|
|
|
|
|
-
Кеңістіктегі вектордың ұзындығы формуласын қолданады
-
Векторлардың коллинеарлық шартын қолданады
-
Векторларды қосу және азайтуды, векторды санға көбейтуді орындайды
-
Векторлардың скаляр көбейтіндісі формуласын қолданады
Ойлау дағдыларының Қолдану
деңгейлері
Орындау уақыты 20 минут
Тапсырма
![]()
-
Егер A(0;1; 2), B(5; 2; 2 ) болса, онда -ның қандай мәнінде AB векторының ұзындығы
 30
болады?
30
болады?
![]()
|
2. |
|
|
|
(0;6; 2) векторларының коллинеар болатынын дәлелдеңіз |
|
a (0;3;1) |
және b |
|||
|
3. |
a 0; 4; 7 |
және b 7; 9; 1 векторлары берілген. 3a 2b және a 4b |
||
|
табыңыз. |
|
|
|
|
![]()
![]()
![]()
![]()
![]()
![]()
-
⃗⃗⃗⃗⃗ = (1; 3; −1) және ⃗⃗⃗⃗⃗ = (4; 2; ) векторлары берілген. Егер = 900 екені белгілі болса, онда − ның мәнін табыңыз.
18
|
Бағалау критерийі |
Тапсырма |
|
Дескриптор |
|
|
Балл |
|||
|
№ |
Білім алушы |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
Кеңістіктегі вектордың |
|
вектор координаталарын өрнектейді |
1 |
||||||
|
ұзындығы формуласын |
|
вектор ұзындығын |
табу |
формуласын |
1 |
||||
|
қолданады |
|
|
|
қолданады |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
-ға қатысты теңдеу құрады |
|
|
1 |
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
теңдеуді шешу тәсілін таңдайды |
|
1 |
|||
|
|
|
|
|
белгісіз айнымалының мәнін табады |
1 |
||||
|
|
|
|
|
|
|
|
|||
|
Векторлардың |
|
|
векторлардың |
коллинеарлық |
шартын |
1 |
|||
|
коллинеарлық |
шартын |
|
қолданады |
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
қолданады |
|
|
2 |
вектордың нөлдік |
емес |
компонентін |
1 |
||
|
|
|
|
табады |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторлардың |
коллинеарлығы |
туралы |
1 |
||
|
|
|
|
|
қорытынды жасайды |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Векторларды |
|
қосу |
|
векторды санға көбейтуді орындайды |
1 |
||||
|
және |
азайтуды, |
|
|||||||
|
3 |
|
|
|
|
|
|
|||
|
векторларды азайтуды орындайды |
1 |
||||||||
|
векторды |
|
санға |
|||||||
|
көбейтуді орындайды |
|
|
|
|
|
|
|
||
|
|
векторларды қосуды орындайды |
|
1 |
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
Векторлардың |
скаляр |
|
векторлардың |
скаляр көбейтіндісінің |
1 |
||||
|
көбейтіндісі |
|
|
|
формуласын қолданады |
|
|
|||
|
|
|
|
|
|
|
||||
|
формуласын |
|
|
4 |
векторлардың перпендикулярлық шартын |
1 |
||||
|
қолданады |
|
|
қолданады |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
белгісіз айнымалының мәнін табады |
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Барлығы: |
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
19
«Кеңістіктегі тікбұрышты координаталар жүйесі және векторлар» бөлімі бойынша жиынтық бағалаудың нәтижесіне қатысты ата-аналарға ақпарат ұсынуға арналған рубрика
Білім алушының аты-жөні: ___________________________________________
|
Бағалау критерийі |
|
|
|
Оқу жетістіктерінің деңгейлері |
|
|
|
|||||||||
|
|
|
|
|
Төмен |
|
|
|
Орта |
|
|
|
Жоғары |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Кеңістіктегі |
вектор |
Кеңістіктегі |
|
|
|
Кеңістіктегі вектордың |
Кеңістіктегі вектордың |
|||||||||
|
ұзындығының |
|
вектордың |
|
|
|
координаталарын |
/ |
|
координаталарын және |
|||||||
|
формуласын |
|
координаталарын |
ұзындығын |
|
табуда |
ұзындығын |
дұрыс |
|||||||||
|
қолданады |
|
және |
ұзындығын |
қателіктер жібереді. |
|
|
табады. |
|
|
|
||||||
|
|
|
|
табуда қиналады. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторлардың |
|
Кеңістіктегі |
|
|
|
Кеңістіктегі коллинеар |
Кеңістіктегі |
|
|
|
||||||
|
коллинеарлық шартын |
векторлардың |
|
|
|
векторлардың |
|
|
|
векторлардың |
|
|
|
||||
|
қолданады |
|
коллинеарлық |
|
|
|
коллинеарлық шартын |
коллинеарлық шартын |
|||||||||
|
|
|
|
шартын қолдануда |
қолдануда |
қателіктер |
дұрыс қолданады. |
||||||||||
|
|
|
|
қиналады. |
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторларды |
қосу |
Векторларды |
қосу |
Векторларды |
қосу |
/ |
|
Векторларды қосу және |
||||||||
|
және |
азайтуды, |
және |
азайтуды, |
азайтуды / |
векторды |
азайтуды, |
векторды |
|||||||||
|
векторды |
|
санға |
векторды |
санға |
санға |
көбейтуді |
санға көбейтуді дұрыс |
|||||||||
|
көбейтуді |
|
көбейтуді |
|
|
|
орындауда |
қателіктер |
орындайды. |
|
|
|
|||||
|
орындайды |
|
орындауда |
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
||
|
|
|
|
қиналады. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторлардың |
|
Векторлардың |
|
|
|
Векторлардың |
скаляр |
Векторлардың |
скаляр |
|||||||
|
скаляр |
көбейтіндісі |
скаляр |
көбейтіндісі |
көбейтіндісі |
|
|
|
|
көбейтіндісі |
|
|
|
||||
|
формуласын |
|
формуласын |
|
|
|
формуласын |
|
|
|
формуласын |
есептер |
|||||
|
қолданады |
|
қолдануда |
|
|
|
қолданады, |
есептеулер |
шығаруда |
дұрыс |
|||||||
|
|
|
|
қиналады. |
|
|
|
жүргізуде |
қателіктер |
қолданады. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
жібереді. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20

шағым қалдыра аласыз

















