
|
«БЕКІТЕМІН» |
«КЕЛІСЕМІН» |
«КЕЛІСЕМІН» |
|
«№93 мектеп-лицей» ШЖҚ МКК директоры. |
директордың оқу ісі жөніндегі орынбасары |
Әдістемелік бірлестік жетекшісі |
|
____________ Б.П. Басықара |
____________ Б. Сыдых |
__________А.К. Хохонай |
|
|
. |
|
Тоқсандық жиынтық бағалау
Сыныбы: 10 «А» «Ә» «Б» «В» «Г»
Мұғалім: Кастен К , Хохонай А.К , Орынбекова Н.Б
Пән: Алгебра және анализ бастамалары
І тоқсан бойынша жиынтық бағалау жасалды.
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
СПЕЦИФИКАЦИЯСЫ
1-тоқсанның жиынтық бағалауына шолу
Ұзақтығы– 40 минут
Балл саны – 25
Тапсырмалар түрлері
ҚЖ – Қысқа жауапты қажет ететінтапсырмалар
ТЖ – Толық жауапты қажет ететін тапсырмалар
Жиынтық бағалаудың құрылымы
Берілген нұсқа қысқа және толық жауапты сұрақтарды қамтитын 6тапсырмадан тұрады.
Қысқа жауапты қажет ететін сұрақтарға білім алушылар есептелген мәні, сөздер немесе қысқа сөйлемдер түрінде жауап береді.
Толық жауапты қажет ететін сұрақтарда білім алушыдан максималды балл жинау үшін тапсырманың шешімін табудың әр
қадамын анық көрсетуі талап етіледі. Білім алушының математикалық тәсілдерді таңдай алу және қолдана алу қабілеті бағаланады. Тапсырма бірнеше құрылымдық бөліктерден/сұрақтардан тұруы мүмкін.
1 -тоқсан бойынша жиынтық бағалау тапсырмаларының сипаттамасы
|
Бөлім |
Тексерілетін мақсат |
Ойлау дағдыла рының деңгейі |
Тапсырма саны* |
№ тапсырма* |
Тапсырм а түрі* |
Орындау уақыты, мин* |
Балл* |
Бөлім бойынша балл |
|
|
Функция, оның қасиеттері және графигі |
10.4.1.4 - функцияның берілген графигі бойынша оның қасиеттерін: 1) функцияның анықталу облысы; 2) функцияның мәндер жиыны; 3) функцияның нөлдері; 4) функцияның периодтылығы; 5) функцияның бірсарындылық аралықтары; 6) функцияның таңбатұрақтылық аралықтары; 7) функцияның ең үлкен және ең кіші мәндері; 8) функцияның жұптылығы,тақтылығы; 9) функцияның шектелгендігі; 10) функция үзіліссіздігі; 11) функцияның экстремумдары сипаттай алу; |
Қолдану |
1 |
3 |
ҚЖ |
4 |
4 |
15 |
|
|
Қолдану |
1 |
6 |
ТЖ |
3 |
2 |
||||
|
10.4.1.5 |
Қолдану |
1 |
5 |
ТЖ |
4 |
4 |
|||
|
|
10.4.1.7 - f(g(x)) күрделі функциясын ажырата білу және функциялар композициясын құру |
Қолдану |
1 |
7 |
ТЖ |
6 |
3 |
||
|
|
10.4.1.6 - кері функцияның анықтамасын білу және берілген функцияға кері функцияны табу және өзара кері функциялар графиктерінің орналасу қасиетін білу; |
Қолдану |
1 |
2 |
ТЖ |
4 |
2 |
||
|
Тригонометрия лық функциялар |
10.2.3.1 - тригонометриялық функциялар анықтамаларын, асиеттерін білу және олардың графиктерін сала білу |
Қолдану |
1 |
4 |
ТЖ |
8 |
4 |
4 |
|
|
10.2.3.2 - тригонометриялық функциялардың графиктерін түрлендірулер көмегімен сала білу |
Қолдану |
||||||||
|
Кері тригонометрия лық функциялар |
10.2.3.3 - арксинус, арккосинус, арктангенс, арккотангенс анықтамаларын білу және олардың мәндерін таба білу |
Білу және түсіну |
1 |
1а |
ТЖ |
6 |
4 |
7 |
|
|
10.2.3.6 - кері тригонометриялық функциялары бар өрнектерді түрлендірулер орындау |
Қолдану |
1 |
1b |
ТЖ |
6 |
3 |
|||
|
Барлығы: |
|
|
7 |
|
|
40 |
|
25 |
|
|
Ескерту: * - өзгертулер енгізуге болатын тараулар |
|
||||||||
І-тоқсан бойынша жиынтық бағалау тапсырмалары Інұсқа
Оқушының аты-жөні _____________________________________ сынып _______
1.a)
2????in  +
3arctg(-
+
3arctg(- ) + arccos(-
) + arccos(-  )
=
)
= [4]
[4]
 b)
cos(2arcsin
b)
cos(2arcsin  )=
[3]
)=
[3]
-
Берілген функцияға кері функцияны жазыңыз:
 -
2;
[2]
-
2;
[2] -
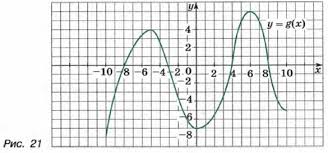
Графигі бойынша функцияның: [4]
|
1 |
Функцияның мәндер жиыны; |
|
|
2 |
Функцияның нөлдері; |
|
-
? = ?in ? функциясының графигін пайдаланып, ? = 3?inx +1функциясының графигін салыңыз [3]
5.
y=
 функциясын ,y=
функциясын ,y=  + n түрінде жазыңызжәне ассимптоталарын
табыңыз.
+ n түрінде жазыңызжәне ассимптоталарын
табыңыз.
[4]
6. Функцияның ең кіші оң периодын
табыңыз: 
 ) + 3 [2]
) + 3 [2]
-
 болса,
болса,  күрделі функциясын
жазыңыз, және
күрделі функциясын
жазыңыз, және  +
+ -ті,
табыңыз.
[3]
-ті,
табыңыз.
[3]
Балл қою кестесі І нұсқа
|
№ |
Жауаптары |
Балл |
Қосымша ақпарат |
|
1a |
????in
|
1 |
|
|
arctg(- |
1 |
|
|
|
arccos(- |
1 |
|
|
|
2∙
|
1 |
|
|
|
1b
|
? − ? ???2(??????
|
1 |
|
|
???2(??????
|
1 |
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
3 1) |
( - ∞; 6] |
1 |
|
|
|
1 |
|
|
|
2) |
|
1 |
|
|
|
1 |
|
|
|
4 |
? = ?in ? функциясының графигін салады |
1 |
|
|
Ордината осі бойымен 3 есе созады |
1 |
|
|
|
Оy осі бойымен 1 бірлікке жоғары жылжытады |
1 |
|
|
|
5 |
y= |
1 |
|
|
y= |
1 |
|
|
|
x=-3 вертикаль ассимптота |
1 |
|
|
|
у =- 2 горизонталь ассимптота |
1 |
|
|
|
6 |
|
1 |
|
|
|
T= |
1 |
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
Барлығы: |
25 |
|
І-тоқсан бойынша жиынтық бағалау тапсырмалары ІІнұсқа
Оқушының аты-жөні _____________________________________ сынып _______
1.a)
3??????  - 4arctg(-1) +
arcsin(-
- 4arctg(-1) +
arcsin(-  )
=
)
= [4]
[4]
 b)
sin(2arccos
b)
sin(2arccos  )=
[3]
)=
[3]
-
Берілген функцияға кері функцияны жазыңыз:
 +5;
[2]
+5;
[2] -
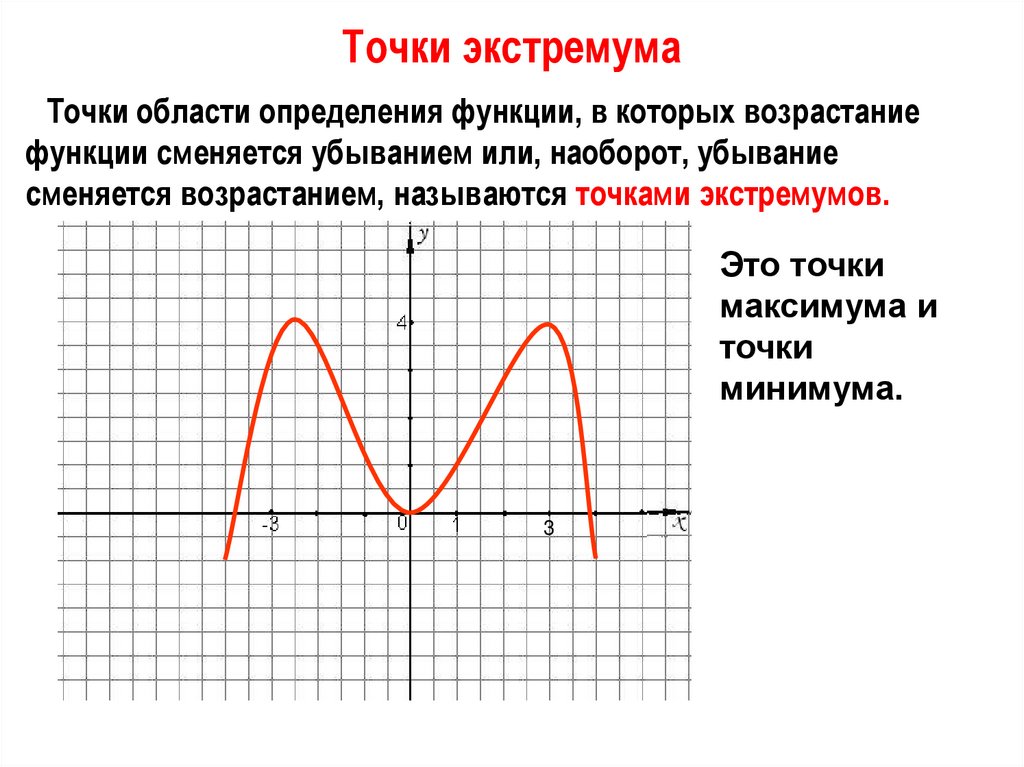
Графигі бойынша функцияның: [4]
|
1 |
Функцияның анықталу облысы; |
|
|
2 |
Функцияның экстремумдары; |
|
-
? = ??? ? функциясының графигін пайдаланып, ? = 2???x -1функциясының графигін салыңыз [3]
5.
y=
 функциясын ,y=
функциясын ,y=  + n түрінде жазыңызжәне ассимптоталарын
табыңыз.
+ n түрінде жазыңызжәне ассимптоталарын
табыңыз.
[4]
6. Функцияның ең кіші оң периодын
табыңыз:  [2]
[2]
7.  болса,
болса,  күрделі функциясын
жазыңыз, және
күрделі функциясын
жазыңыз, және  +
+  -ті, табыңыз.
[3]
-ті, табыңыз.
[3]
Балл қою кестесі ІІ нұсқа
|
№ |
Жауаптары |
Балл |
Қосымша ақпарат |
|
1a |
?????? |
1 |
|
|
arctg(-1)= -
|
1 |
|
|
|
arcsin(- |
1 |
|
|
|
3∙
|
1 |
|
|
|
1b
|
? ??? (?????? |
1 |
|
|
???(?????? |
1 |
|
|
|
? ∙ |
1 |
|
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
3 1) |
( - ∞; ∞) |
1 |
|
|
Хmax=-2,5 |
1 |
|
|
|
2) |
Хmax= 3 |
1 |
|
|
Хmin= 0 |
1 |
|
|
|
4 |
? = ??? ?функциясының графигін салады |
1 |
|
|
Ордината осі бойымен 2 есе созады |
1 |
|
|
|
Оу осі бойымен 1 бірлікке төмен жылжытады |
1 |
|
|
|
5 |
y= |
1 |
|
|
y= |
1 |
|
|
|
x=3 вертикаль ассимптота |
1 |
|
|
|
у = 2 горизонталь ассимптота |
1 |
|
|
|
6 |
|
1 |
|
|
T= |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
Барлығы: |
25 |
|
І-тоқсан бойынша жиынтық бағалау тапсырмалары ІІІ нұсқа
Оқушының аты-жөні _____________________________________ сынып _______
1.a)
4
??????  - 2arctg(-1) +
arcsin(-
- 2arctg(-1) +
arcsin(-  )
=
)
= [4]
[4]
 b)
sin(2arccos
b)
sin(2arccos  )=
[3]
)=
[3]
2Берілген функцияға
кері функцияны жазыңыз:  -3;
[2]
-3;
[2]
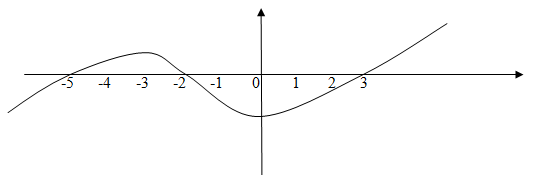
3.Графигі бойынша функцияның: [4]
|
1 |
таңба-тұрақтылық аралықтарын; |
|
|
2 |
өсу және кему аралықтарын ;
|
|
-
? = ??? ? функциясының графигін пайдаланып, ? = 3???x +1функциясының графигін салыңыз [3]
5.
y=
 функциясын ,y=
функциясын ,y=  + n түрінде жазыңызжәне ассимптоталарын
табыңыз.
+ n түрінде жазыңызжәне ассимптоталарын
табыңыз.
[4]
6. Функцияның ең кіші оң периодын
табыңыз:  [2]
[2]
7.  болса,
болса,  күрделі функциясын
жазыңыз, және
күрделі функциясын
жазыңыз, және  +
+  -ті, табыңыз.
[3]
-ті, табыңыз.
[3]
Балл қою кестесі ІІІ нұсқа
|
№ |
Жауаптары |
Балл |
Қосымша ақпарат |
|
1a |
?????? |
1 |
|
|
arctg(-1)= -
|
1 |
|
|
|
arcsin(- |
1 |
|
|
|
4∙
|
1 |
|
|
|
1b
|
? ??? (?????? |
1 |
|
|
???(?????? |
1 |
|
|
|
? ∙ |
1 |
|
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
3 1) |
? ∈ (−?; −?)∪(3; ∞) аралығында y> 0 |
1 |
|
|
? ∈ (−∞; −?) ∪ (−?; ?)аралығында y< 0 |
1 |
|
|
|
2) |
? ∈ (−∞; −?) ∪ (?; +∞)аралығында функция өседі |
1 |
|
|
? ∈ (−?; ?)аралығында функция кемиді |
1 |
|
|
|
4 |
? = ??? ?функциясының графигін салады |
1 |
|
|
Ордината осі бойымен 3 есе созады |
1 |
|
|
|
Оу осі бойымен 1 бірлікке жоғары жылжытады |
1 |
|
|
|
5 |
y= |
1 |
|
|
y= |
1 |
|
|
|
x=2 вертикаль ассимптота |
1 |
|
|
|
у = 3 горизонталь ассимптота |
1 |
|
|
|
6 |
|
1 |
|
|
T= |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
Барлығы: |
25 |
|
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
10сынып ТЖБ-1 алгебра
10сынып ТЖБ-1 алгебра
|
«БЕКІТЕМІН» |
«КЕЛІСЕМІН» |
«КЕЛІСЕМІН» |
|
«№93 мектеп-лицей» ШЖҚ МКК директоры. |
директордың оқу ісі жөніндегі орынбасары |
Әдістемелік бірлестік жетекшісі |
|
____________ Б.П. Басықара |
____________ Б. Сыдых |
__________А.К. Хохонай |
|
|
. |
|
Тоқсандық жиынтық бағалау
Сыныбы: 10 «А» «Ә» «Б» «В» «Г»
Мұғалім: Кастен К , Хохонай А.К , Орынбекова Н.Б
Пән: Алгебра және анализ бастамалары
І тоқсан бойынша жиынтық бағалау жасалды.
1-ТОҚСАН БОЙЫНША ЖИЫНТЫҚ БАҒАЛАУ
СПЕЦИФИКАЦИЯСЫ
1-тоқсанның жиынтық бағалауына шолу
Ұзақтығы– 40 минут
Балл саны – 25
Тапсырмалар түрлері
ҚЖ – Қысқа жауапты қажет ететінтапсырмалар
ТЖ – Толық жауапты қажет ететін тапсырмалар
Жиынтық бағалаудың құрылымы
Берілген нұсқа қысқа және толық жауапты сұрақтарды қамтитын 6тапсырмадан тұрады.
Қысқа жауапты қажет ететін сұрақтарға білім алушылар есептелген мәні, сөздер немесе қысқа сөйлемдер түрінде жауап береді.
Толық жауапты қажет ететін сұрақтарда білім алушыдан максималды балл жинау үшін тапсырманың шешімін табудың әр
қадамын анық көрсетуі талап етіледі. Білім алушының математикалық тәсілдерді таңдай алу және қолдана алу қабілеті бағаланады. Тапсырма бірнеше құрылымдық бөліктерден/сұрақтардан тұруы мүмкін.
1 -тоқсан бойынша жиынтық бағалау тапсырмаларының сипаттамасы
|
Бөлім |
Тексерілетін мақсат |
Ойлау дағдыла рының деңгейі |
Тапсырма саны* |
№ тапсырма* |
Тапсырм а түрі* |
Орындау уақыты, мин* |
Балл* |
Бөлім бойынша балл |
|
|
Функция, оның қасиеттері және графигі |
10.4.1.4 - функцияның берілген графигі бойынша оның қасиеттерін: 1) функцияның анықталу облысы; 2) функцияның мәндер жиыны; 3) функцияның нөлдері; 4) функцияның периодтылығы; 5) функцияның бірсарындылық аралықтары; 6) функцияның таңбатұрақтылық аралықтары; 7) функцияның ең үлкен және ең кіші мәндері; 8) функцияның жұптылығы,тақтылығы; 9) функцияның шектелгендігі; 10) функция үзіліссіздігі; 11) функцияның экстремумдары сипаттай алу; |
Қолдану |
1 |
3 |
ҚЖ |
4 |
4 |
15 |
|
|
Қолдану |
1 |
6 |
ТЖ |
3 |
2 |
||||
|
10.4.1.5 |
Қолдану |
1 |
5 |
ТЖ |
4 |
4 |
|||
|
|
10.4.1.7 - f(g(x)) күрделі функциясын ажырата білу және функциялар композициясын құру |
Қолдану |
1 |
7 |
ТЖ |
6 |
3 |
||
|
|
10.4.1.6 - кері функцияның анықтамасын білу және берілген функцияға кері функцияны табу және өзара кері функциялар графиктерінің орналасу қасиетін білу; |
Қолдану |
1 |
2 |
ТЖ |
4 |
2 |
||
|
Тригонометрия лық функциялар |
10.2.3.1 - тригонометриялық функциялар анықтамаларын, асиеттерін білу және олардың графиктерін сала білу |
Қолдану |
1 |
4 |
ТЖ |
8 |
4 |
4 |
|
|
10.2.3.2 - тригонометриялық функциялардың графиктерін түрлендірулер көмегімен сала білу |
Қолдану |
||||||||
|
Кері тригонометрия лық функциялар |
10.2.3.3 - арксинус, арккосинус, арктангенс, арккотангенс анықтамаларын білу және олардың мәндерін таба білу |
Білу және түсіну |
1 |
1а |
ТЖ |
6 |
4 |
7 |
|
|
10.2.3.6 - кері тригонометриялық функциялары бар өрнектерді түрлендірулер орындау |
Қолдану |
1 |
1b |
ТЖ |
6 |
3 |
|||
|
Барлығы: |
|
|
7 |
|
|
40 |
|
25 |
|
|
Ескерту: * - өзгертулер енгізуге болатын тараулар |
|
||||||||
І-тоқсан бойынша жиынтық бағалау тапсырмалары Інұсқа
Оқушының аты-жөні _____________________________________ сынып _______
1.a)
2????in  +
3arctg(-
+
3arctg(- ) + arccos(-
) + arccos(-  )
=
)
= [4]
[4]
 b)
cos(2arcsin
b)
cos(2arcsin  )=
[3]
)=
[3]
-
Берілген функцияға кері функцияны жазыңыз:
 -
2;
[2]
-
2;
[2] -
Графигі бойынша функцияның: [4]
|
1 |
Функцияның мәндер жиыны; |
|
|
2 |
Функцияның нөлдері; |
|

-
? = ?in ? функциясының графигін пайдаланып, ? = 3?inx +1функциясының графигін салыңыз [3]
5.
y=
 функциясын ,y=
функциясын ,y=  + n түрінде жазыңызжәне ассимптоталарын
табыңыз.
+ n түрінде жазыңызжәне ассимптоталарын
табыңыз.
[4]
6. Функцияның ең кіші оң периодын
табыңыз: 
 ) + 3 [2]
) + 3 [2]
-
 болса,
болса,  күрделі функциясын
жазыңыз, және
күрделі функциясын
жазыңыз, және  +
+ -ті,
табыңыз.
[3]
-ті,
табыңыз.
[3]
Балл қою кестесі І нұсқа
|
№ |
Жауаптары |
Балл |
Қосымша ақпарат |
|
1a |
????in
|
1 |
|
|
arctg(- |
1 |
|
|
|
arccos(- |
1 |
|
|
|
2∙
|
1 |
|
|
|
1b
|
? − ? ???2(??????
|
1 |
|
|
???2(??????
|
1 |
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
3 1) |
( - ∞; 6] |
1 |
|
|
|
1 |
|
|
|
2) |
|
1 |
|
|
|
1 |
|
|
|
4 |
? = ?in ? функциясының графигін салады |
1 |
|
|
Ордината осі бойымен 3 есе созады |
1 |
|
|
|
Оy осі бойымен 1 бірлікке жоғары жылжытады |
1 |
|
|
|
5 |
y= |
1 |
|
|
y= |
1 |
|
|
|
x=-3 вертикаль ассимптота |
1 |
|
|
|
у =- 2 горизонталь ассимптота |
1 |
|
|
|
6 |
|
1 |
|
|
|
T= |
1 |
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
Барлығы: |
25 |
|
І-тоқсан бойынша жиынтық бағалау тапсырмалары ІІнұсқа
Оқушының аты-жөні _____________________________________ сынып _______
1.a)
3??????  - 4arctg(-1) +
arcsin(-
- 4arctg(-1) +
arcsin(-  )
=
)
= [4]
[4]
 b)
sin(2arccos
b)
sin(2arccos  )=
[3]
)=
[3]
-
Берілген функцияға кері функцияны жазыңыз:
 +5;
[2]
+5;
[2] -
Графигі бойынша функцияның: [4]
|
1 |
Функцияның анықталу облысы; |
|
|
2 |
Функцияның экстремумдары; |
|

-
? = ??? ? функциясының графигін пайдаланып, ? = 2???x -1функциясының графигін салыңыз [3]
5.
y=
 функциясын ,y=
функциясын ,y=  + n түрінде жазыңызжәне ассимптоталарын
табыңыз.
+ n түрінде жазыңызжәне ассимптоталарын
табыңыз.
[4]
6. Функцияның ең кіші оң периодын
табыңыз:  [2]
[2]
7.  болса,
болса,  күрделі функциясын
жазыңыз, және
күрделі функциясын
жазыңыз, және  +
+  -ті, табыңыз.
[3]
-ті, табыңыз.
[3]
Балл қою кестесі ІІ нұсқа
|
№ |
Жауаптары |
Балл |
Қосымша ақпарат |
|
1a |
?????? |
1 |
|
|
arctg(-1)= -
|
1 |
|
|
|
arcsin(- |
1 |
|
|
|
3∙
|
1 |
|
|
|
1b
|
? ??? (?????? |
1 |
|
|
???(?????? |
1 |
|
|
|
? ∙ |
1 |
|
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
3 1) |
( - ∞; ∞) |
1 |
|
|
Хmax=-2,5 |
1 |
|
|
|
2) |
Хmax= 3 |
1 |
|
|
Хmin= 0 |
1 |
|
|
|
4 |
? = ??? ?функциясының графигін салады |
1 |
|
|
Ордината осі бойымен 2 есе созады |
1 |
|
|
|
Оу осі бойымен 1 бірлікке төмен жылжытады |
1 |
|
|
|
5 |
y= |
1 |
|
|
y= |
1 |
|
|
|
x=3 вертикаль ассимптота |
1 |
|
|
|
у = 2 горизонталь ассимптота |
1 |
|
|
|
6 |
|
1 |
|
|
T= |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
Барлығы: |
25 |
|
І-тоқсан бойынша жиынтық бағалау тапсырмалары ІІІ нұсқа
Оқушының аты-жөні _____________________________________ сынып _______
1.a)
4
??????  - 2arctg(-1) +
arcsin(-
- 2arctg(-1) +
arcsin(-  )
=
)
= [4]
[4]
 b)
sin(2arccos
b)
sin(2arccos  )=
[3]
)=
[3]
2Берілген функцияға
кері функцияны жазыңыз:  -3;
[2]
-3;
[2]
3.Графигі бойынша функцияның: [4]
|
1 |
таңба-тұрақтылық аралықтарын; |
|
|
2 |
өсу және кему аралықтарын ;
|
|

-
? = ??? ? функциясының графигін пайдаланып, ? = 3???x +1функциясының графигін салыңыз [3]
5.
y=
 функциясын ,y=
функциясын ,y=  + n түрінде жазыңызжәне ассимптоталарын
табыңыз.
+ n түрінде жазыңызжәне ассимптоталарын
табыңыз.
[4]
6. Функцияның ең кіші оң периодын
табыңыз:  [2]
[2]
7.  болса,
болса,  күрделі функциясын
жазыңыз, және
күрделі функциясын
жазыңыз, және  +
+  -ті, табыңыз.
[3]
-ті, табыңыз.
[3]
Балл қою кестесі ІІІ нұсқа
|
№ |
Жауаптары |
Балл |
Қосымша ақпарат |
|
1a |
?????? |
1 |
|
|
arctg(-1)= -
|
1 |
|
|
|
arcsin(- |
1 |
|
|
|
4∙
|
1 |
|
|
|
1b
|
? ??? (?????? |
1 |
|
|
???(?????? |
1 |
|
|
|
? ∙ |
1 |
|
|
|
2 |
|
1 |
|
|
|
1 |
|
|
|
3 1) |
? ∈ (−?; −?)∪(3; ∞) аралығында y> 0 |
1 |
|
|
? ∈ (−∞; −?) ∪ (−?; ?)аралығында y< 0 |
1 |
|
|
|
2) |
? ∈ (−∞; −?) ∪ (?; +∞)аралығында функция өседі |
1 |
|
|
? ∈ (−?; ?)аралығында функция кемиді |
1 |
|
|
|
4 |
? = ??? ?функциясының графигін салады |
1 |
|
|
Ордината осі бойымен 3 есе созады |
1 |
|
|
|
Оу осі бойымен 1 бірлікке жоғары жылжытады |
1 |
|
|
|
5 |
y= |
1 |
|
|
y= |
1 |
|
|
|
x=2 вертикаль ассимптота |
1 |
|
|
|
у = 3 горизонталь ассимптота |
1 |
|
|
|
6 |
|
1 |
|
|
T= |
1 |
|
|
|
7 |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
Барлығы: |
25 |
|

шағым қалдыра аласыз



































































